浙江省湖州市长兴县2019-2020学年七年级上学期数学第三次月考试卷
试卷更新日期:2019-12-24 类型:月考试卷
一、选择题(每小题3分,共30分)
-
1. 实数-4的绝对值是( )A、 B、-4 C、 D、42. 年 月 日 时 分,“嫦娥四号”探测器飞行约 千米,实现人类探测器首次在月球背面软着陆.数据 用科学记数法表示为( )A、 B、 C、 D、3. 计算2a-3a,结果正确的是( )A、-a B、a C、-1 D、14. 下列方程中,解为x=-2的方程是( )A、x-2=0 B、2+3x=-4 C、3x-1=2 D、4-2x=35. 某地一周前四天每天的最高气温与最低气温如表,则这四天中温差最大的是( )
星期
一
二
三
四
最高气温
10℃
12℃
11℃
9℃
最低气温
3℃
0℃
-2℃
-3℃
A、星期一 B、星期二 C、星期三 D、星期四6. 关于 的叙述正确的是( )A、在数轴上不存在表示 的点 B、 可是有理数 C、 介于整数3和4之间 D、面积是8的正方形边长是7. 如图,将刻度尺放在数轴上(数轴的单位长度是1cm),刻度尺上“0cm”和“3cm”分别对应数轴上的3和0,那么刻度尺上“5.4cm”对应数轴上的数为( ) A、5.4 B、-2.4 C、-2.6 D、-1.68. 已知九年级某班30位学生种树72棵,男生每人种3棵树,女生每人种2棵树。设男生有x人,则( )A、3x+2(30-x)=72 B、3x+2(72-x)=30 C、2x+3(30-x)=72 D、2x+3(72-x)=309. 已知m-n=100,x+y=-1,则代数式(n+x)-(m-y)的值为( )A、99 B、-99 C、-101 D、10110. 古巴比伦的记数法是六十进制的,用
A、5.4 B、-2.4 C、-2.6 D、-1.68. 已知九年级某班30位学生种树72棵,男生每人种3棵树,女生每人种2棵树。设男生有x人,则( )A、3x+2(30-x)=72 B、3x+2(72-x)=30 C、2x+3(30-x)=72 D、2x+3(72-x)=309. 已知m-n=100,x+y=-1,则代数式(n+x)-(m-y)的值为( )A、99 B、-99 C、-101 D、10110. 古巴比伦的记数法是六十进制的,用 表示1,用
表示1,用 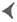 表示10,这两种符号能表示一直到59的数字,例如,32可以用
表示10,这两种符号能表示一直到59的数字,例如,32可以用 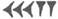 表示。从60起,开始使用符号组,从右往左依次是个位、六十位、三千六百位……(每一位的数值都是上一位的60倍),例如,
表示。从60起,开始使用符号组,从右往左依次是个位、六十位、三千六百位……(每一位的数值都是上一位的60倍),例如, 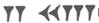 的个位表示23个1,六十位表示2个60,所以这个符号表示143。则下列表示3812的符号是( ) A、
的个位表示23个1,六十位表示2个60,所以这个符号表示143。则下列表示3812的符号是( ) A、 B、
B、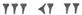 C、
C、 D、
D、
二、填空题(每小题2分,共12分)
-
11. 单项式-2x2y的系数是。12. 若一个数的平方等于5,则这个数是 。13. 用代数式表示:“x的2倍与y的差的平方”是 .14. 数轴上有两个实数a,b,且a>0,b<0,a+b<0,则四个数a,b,-a,-b中最大的是。15. 书店举行购书优惠活动:
①一次性购书不超过100元,不享受打折优惠;
②一次性购书超过100元但不超过200元一律打九折;
③一次性购书超过200元一律打七折.
小丽在这次活动中,两次购书总共付款229.4元,第二次购书原价是第一次购书原价的3倍,那么小丽这两次购书原价的总和是元.
16. 砸“金蛋”游戏:把210个“金蛋”连续编号为1,2,3,…,210,接着把编号是3的整数倍的“金蛋”全部砸碎;然后将剩下的“金蛋”重新连续编号为1,2,3,…,接着把编号是3的整数倍的“金蛋”全部砸碎……按照这样的方法操作,直到无编号是3的整数倍的“金蛋”为止.操作过程中砸碎编号是“60”的“金蛋”共个。三、解答题(共58分)
-
17. 把下列各数的序号填到相应的横线上:
① ,② ,③ ,④0,⑤π,⑥-3.14,⑦2.9,⑧1.3030030003…(每两个3之间多一个0)。
整数:;
负分数:;
无理数:。
18. 计算。(1)、( )×2+3(2)、22+(-3)2÷19. 解方程:(1)、5x=3x-4(2)、10+2(x- )=7(x-2)20. 先化简,再求值:3(2a2+ab)-2(3a2+ab),其中a=-2,b=3。21. 定义新运算:a★b=a(1-b),a,b是实数。如-2★3=-2×(1-3)=4.(1)、求(-2)★(-1)的值;(2)、求2★ +2★(- )的值。22. 已知方程 与关于x的方程3a-8=2(x+a)-a的解相同。(1)、求方程的解;(2)、求a的值。23. 已知代数式ax5+bx3+3x+c“当x=0时,该代数式的值为-1。(1)、求c的值;(2)、已知当x=1时.该代数式的值为-1,试求a+b+c的值;(3)、已知当x=3时,该代数式的值为9,试求当x=-3时该代数式的值。24. 为提高市民的环保意识,倡导“节能减排,绿色出行”,某市计划在城区投放一批“共享单车”这批单车分为A,B两种不同款型,其中A型车单价400元,B型车单价320元。(1)、今年年初,“共享单车”试点投放在某市中心城区正式启动,投放A,B两种款型的单车共100辆,总价值36800元,试问本次试点投放的A型车与B型车各多少辆?(2)、试点投放活动得到了广大市民的认可,该市决定将此项公益活动在整个城区全面铺开,按照试点投放中A,B两车型的数量比进行投放.且投资总价值达到184万元,请问投放后城区有A型车与B型车各多少辆?