浙江省湖州市长兴县2019-2020学年八年级上学期数学第三次月考试卷
试卷更新日期：2019-12-24 类型：月考试卷
一、选择题(每小题3分，共30分)
-
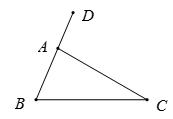
1. 函数y= 中，自变量x的取值范围是（ ）A、x=-2 B、x=1 C、x≠-2 D、x≠12. 如图，在△ABC中，∠B=70°，∠C=30°，则∠DAC的度数为（ ）
A、100° B、110° C、150° D、80°3. 不等式6+3x>2x的解是 （ ）A、x>6 B、x<6 C、x>-6 D、x<-64. 在Rt△ABC中，∠C=90°，AB=10，AC=8，则BC=（ ）A、6 B、8 C、10 D、5. 说明命题“ =a”是假命题的一个正确的反例是（ ）A、a=3 B、a=-3 C、a=0.3 D、a=06. 如图，△ABC的边AC的中垂线与∠BAC的角平分线交于点O，已知OE=2，则点O到AB的距离为（ ）
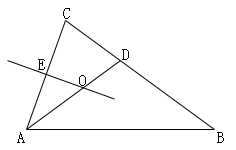A、2 B、3 C、4 D、57. 如图，在△ABC中，2BD=3DC，E是AC的中点，如S△ABC=10，则S△ADE=（ ）
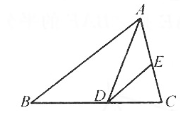A、5 B、4 C、3 D、28. 湖州与杭州之间的高速路程为s，汽车行驶的平均速度为v，驶完这段路程所需的时间为t，则s=vt，其中常量（ ）A、为v B、为s C、为t D、没有9. 等腰三角形ABC的周长为10，底边BC长为y，腰AB长为x，则x的取值范围是（ ）A、5<x<10 B、0<x<5 C、2.5<x<5 D、1.25<x<2.510. 勾股定理是人类最伟大的科学发现之一，在我国古算书《周髀算经》中早有记载，如图1，以直角三角形的各边为边分别向外作正方形，再把较小的两张正方形纸片按图2的方式放置在最大正方形内．若知道图中阴影部分的面积，则一定能求出（ ）
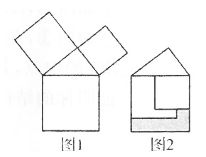A、直角三角形的面积 B、最大正方形的面积 C、较小两个正方形重叠部分的面积 D、最大正方形与直角三角形的面积和二、填空题(每小题4分，共24分)
-
11. 不等式组 的解为。12. 已知点A(-2，4)，则点A关于y轴的对称点A'的坐标为。13. 已知等边三角形的边长为4，则它的一边上的高线长为。14. 如图，在△ABC和△DEF中，点B，F，C，E在同一直线上，BF=CE，AB∥DE，请添加一个条件，使△ABC≌△DEF，这个添加的条件可以是 (只需写一个，不添辅助线)。
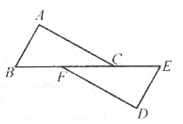15. 如图，在Rt△ABC中，∠ACB=90°，AD平分∠CAB，交CB于点D，DE⊥AB，垂足为E．若AC=3，AB=5，则DE的长为。
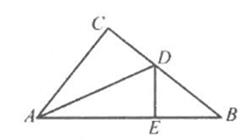16. 如图，在平面直角坐标系中，等腰直角三角形OAA1的直角边OA在x轴上，点A1在第一象限，且OA=1，以点A1为直角顶点，OA1为一直角边作等腰直角三角形OA1A2 ， 再以点A2为直角顶点，OA2为直角边作等腰直角三角形OA2A3…依此规律，则点A2019的坐标是 ．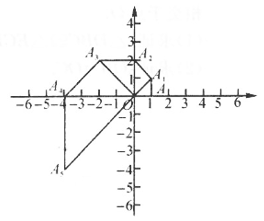
三、解答题(共66分)
-
17. 解下列不等式(组)：(1)、(2)、18. 在等腰△ABC中，AB=AC=10，BC=12，求BC边上的高线AD的长。
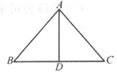19. 已知关于x的方程 的解是不等式2x+a>0的一个解，求a的取值范围。20. 如图，在△ABC中，AB=AC，点D，E分别在AB，AC上，BD=CE，BE与CD相交于点O。
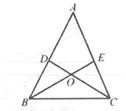(1)、求证；△DBC≌△ECB；(2)、求证：OB=OC。21. 如图，在Rt△ABC中，∠ACB=90°，CD⊥AB于点D，点E，F分别是BC，AC的中点。
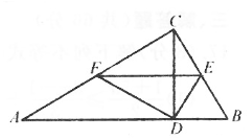(1)、求证：DF⊥DE(2)、若AC=8，BC=6，求EF的长。22. 某商店A型号笔记本电脑的售价是a元／台，最近，该商店对A型号笔记本电脑举行促销活动，有两种优惠方案，方案一：每台按售价的九折销售；方案二；若购买不超过5台，每台按售价销售；若超过5台，超过的部分每台按售价的八折销售。某公司一次性从该商店购买A型号笔记本电脑x台。(1)、当x=8时，应选择哪种方案，该公司购买费用最少?最少费用是多少元?(2)、若该公司采用方案二购买更合算，求x的取值范围。23. 如图，每个小方格的边长为1，已知点A(2，2)，把点A先向左平移4个单位，再向下平移2个单位到达点B；把点B先向右平移2个单位，再向下平移4个单位到达点C。
(1)、在图中画出△ABC，并直接写出B，C两点的坐标：B（ ），C（ ）；(2)、求△ABC的面积；(3)、判断△ABC的形状，并说明理由。24. 如图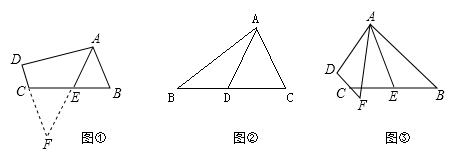
(1)、如图①，在四边形ABCD中，AB∥CD，点E是BC的中点，若AE是∠BAD的平分线，试判断AB，AD，DC之间的等量关系。解决此问题可以用如下方法：延长AE交DC的延长线于点F，易证△AEB≌△FEC得到AB=FC，从而把AB，AD，DC转化在一个三角形中即可判断。
AB，AD，DC之间的等量关系；
(2)、同题探究；①如图②，AD是△ABC的中线，AB=6，AC=4，求AD的范围：
②如图③，在四边形ABCD中，AB∥CD，AF与DC的延长线交于点F，点E是BC的中点，若AE是∠BAF的平分线，试探究AB，AF，CF之间的等量关系，并证明你的结论。