浙江省“温州新希蓝联盟校”九年级上学期数学第四次联考试卷
试卷更新日期：2019-12-24 类型：月考试卷
一、选择题(本题有10小题．每小题4分，共40分)
-
1. 已知3x=5y，则 =（ ）A、 B、 C、 D、2. 抛物线砷y=x2+6x+8与y轴交点坐标（ ）A、(0，8) B、(0，-8) C、(0，6) D、(0，-6)3. 如图，△ABC内接于⊙O中，AB=AC， =60°，则∠B=（ ）
A、30° B、45° C、60° D、75°4. 下列事件中，属于随机事件的是（ ）A、上抛的硬币会落下 B、太阳从西边升起 C、明年元旦是晴天 D、一匹马的奔跑速度是700米／秒5. 一个圆的内接正多边形中，一边所对的圆心角为72°，则该正多边形的边数是（ ）A、6 B、5 C、4 D、36. 已知扇形的弧长为8π，圆心角为120°，则扇形的半径是（ ）A、6 B、8 C、12 D、247. 如图．直线l1∥l2∥l3 ， 直线AC分别交l1 ， l2 ， l3于点A，B，C；直线DF分别交l1 ， l2 ， l3于点D，E，F；AC与DF相交于点H，且AH=4，HB=2，BC=10，则 =（ ）
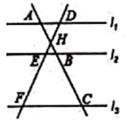A、 B、2 C、 D、8. 二次函数y=(x-4)(x+2)图象的顶点坐标是（ ）A、(4，0) B、(-1，-5) C、(1，-9) D、(1，9)9. 如图，AB和CD表示两根直立于地面的柱子，AC和BD表示起固定作用的两根钢筋，AC与BD相交于点M，已知AB=8m，CD=12m，则点M离地面的高度MH为（ ）
A、4 m B、 m C、5m D、 m10. 我们知道，勾股定理反映了直角三角形三条边的关系：a2+b2=c2 ， 而a2 ， b2 ， c2又可以看成是以a，b，c为边长的正方形的面积。如图，在Rt△ABC中，∠ACB=90°，BC=a，AC=b，O为AB的中点，分别以AC，BC为边向△ABC外作正方形ACFG，BCED，连结OF，EF，OE，则△OEF的面积为（ ）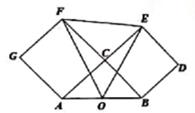
A、 B、 C、 D、二、填空题(本题有6小题．每小题5分，共30分)
-
11. 若 ，则 = ．12. 有10个杯子，其中一等品7个，二等品3个，任意取一个杯子，是一等品的概率是。13. 已知弦AB把圆周分成1：5的两部分，则弦AB所对的圆心角的度数为度。14. 将抛物线y=x2-12x+16作关于X轴对称．所得抛物线的解析式是。15. 如图，在△ABC中，AC=BC=5，AB=6，点D为AC上一点，作DE∥AB交BC于点E，点C关于DE的对称点为点O，以OA为半径作⊙O恰好经过点C，并交直线DE于点M，N，则MN的值为。
16. 3个边长为1的小正方形拼成的图形如图所示，P是其中两个小正方形的公共顶点，且点A，B，P三点共线，现将该图形沿着过点P的某条直线剪一刀，使剪痕两侧的面积相等，则剪痕的长度是。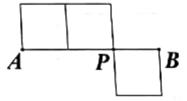
三、解答题(本题有8小题，共80分．)
-
17.
(1)、求x的值：5：（x+1)=3：x。(2)、已知线段a=2，b=8，求a，b的比例中项线段c。18. 在△ABC，AB=AC，在BC上取点E，连结AE并延长至点D，使得∠D=∠C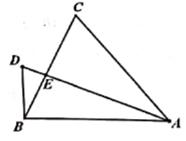
(1)、求证：△ABE∽△ADB。(2)、若DE=1，AE=5，求AC的长。19. 一个不透明的袋中只装有1个红球和2个白球，它们除颜色外其余均相同，现随机从袋中摸出两个球。(1)、求两次摸出的球恰好颜色不同的概率(要求画树状图或列表)。(2)、现再将n个红球放入布袋，搅均后，使摸出1个球是红球的概率为 ，求n的值。20. 如图，线段AB的两个端点都在正方形格点上，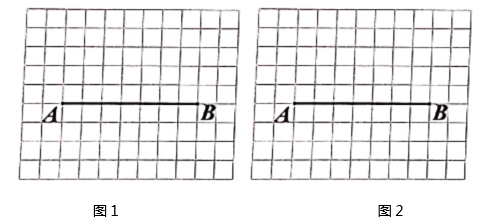
按要求作图：
①仅用一把无刻度直尺；②保留能够体现你画法的作图痕迹。
(1)、在图1中画出线段AB的二等分点C。(2)、在图2中画出线段AB的一个三等分点D。21. 在平面直角坐标系中，△AOB的位置如图所示，∠AOB=90°，AO=BO，点A的坐标为(-1，2)，抛物线y=ax2+bx(a≠0)恰好经过A，B两点。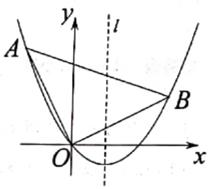
(1)、直接写出点B坐标。(2)、求该抛物线的函数表达式。(3)、设A关于抛物线的对称轴l的对称点为A'，求△AA'B的面积。22. 如图，△ABC内接于⊙O，∠ABC和∠BAC的平分线交于点E，延长AE分别交BC，⊙O于点F，D，连接BD。
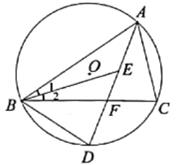(1)、求证：BD=DE。(2)、若BD=6，AD=10，求EF的长。23. 某宾馆有若干间标准客房，当房价为200元/间时，日均入住数为60间，市场调查表明，在物价局核定的每间标准房价格在160～220元之间(含160元，220元)浮动时，每提高10元，日均入住数减少10间，在不考虑其他因素的前提下，设标准房的价格为x元／间，日均入住数为y间。(1)、y关于x的解析式为。(2)、当标准房的价格定为多少元时．客房的日营业额为10500元?(3)、当标准房的价格定为多少元时，客房的日营业额最大，最大为多少元?24. 如图1，正方形ABCD的边长为4，点E，F分别在BC，BD上，且BE=1，过三点C，E，F作⊙O交CD于点G。
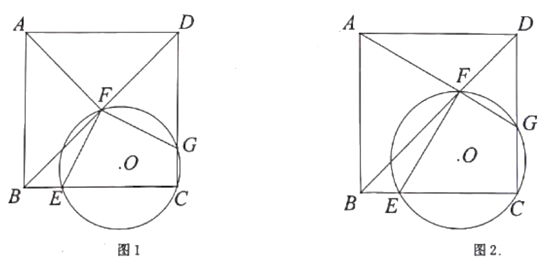(1)、证明∠EFG=90°．(2)、如图2，连结AF，当点F运动至点A，F，G三点共线时，求△ADF的面积。(3)、在点F整个运动过程中，①当EF，FG，CG中满足某两条线段相等，求所有满足条件的BF的长。
②连接EG，若 时，求⊙O的半径(请直接写出答案)。