浙江省瑞安市2019届初中毕业升学考试适应性测试卷数学中考三模试卷

试卷更新日期：2019-12-24 类型：中考模拟

进入出卷网下载

一、单选题

1. 在﹣4，2，0，﹣3这四个数中，最小的数是（　　）

A、﹣4 B、2 C、0 D、﹣3

查看试题解析
2. 如图，几何体的左视图是（　　）

A、 B、 C、 D、

查看试题解析
3. 计算x⁶÷x²的结果是（　　）

A、x¹² B、x⁸ C、x⁴ D、x³

查看试题解析
4. 不等式4x+1＞–1的解是（）

A、x<– $\frac{1}{2}$ B、x＞– $\frac{1}{2}$ C、x＞–2 D、x<–2

查看试题解析
5. 在一次中学生田径运动会上，参加男子跳高的20名运动员的成绩如下表所示：

成绩 $($ 米 $)$

$1.55$

$1.60$

$1.65$

$1.70$

$1.75$

$1.80$

人数

4

3

5

6

1

1

则这些运动员成绩的众数为 $($ 　　 $)$

A、 $1.55$ 米 B、 $1.65$ 米 C、 $1.70$ 米 D、 $1.80$ 米

查看试题解析
6. 若分式 $\frac{x^{2} - 9}{x + 3}$ 的值为零，则x值为（　　）

A、x＝±3 B、x＝0 C、x＝﹣3 D、x＝3

查看试题解析
7. 某校九年级师生共466人，准备组织去某地参加综合社会实践活动.现已预备了37座和49座两种客车共10辆，刚好坐满.设37座客车a辆，49座客车b辆，根据题意可列出方程组为（　　）

A、 ${\begin{cases} a + b = 10 \\ 37 a + 49 b = 466 \end{cases}$ B、 ${\begin{cases} a + b = 10 \\ 49 a + 37 b = 466 \end{cases}$ C、 ${\begin{cases} a + b = 466 \\ 37 a + 49 b = 10 \end{cases}$ D、 ${\begin{cases} a + b = 466 \\ 49 a + 37 b = 10 \end{cases}$

查看试题解析
8. 如图，在平面直角坐标系中，点A、B的坐标分别为（0，4）和（1，3），△OAB沿x轴向右平移后得到△O′A′B′，点A的对应点A在直线y＝ $\frac{5}{4}$ x﹣1上，则点B与点O′之间的距离为（　　）

A、3 B、4 C、3 $\sqrt{2}$ D、 $\sqrt{34}$

查看试题解析
9. 如图，小靓用七巧板拼成一幅装饰图，放入长方形ABCD内，装饰图中的三角形顶点E，F分别在边AB，BC上，△GHD的边GD在边AD上，则 $\frac{A B}{B C}$ 的值为（　　）

A、 $\frac{1 + \sqrt{2}}{4}$ B、4 $\sqrt{2}$ ﹣4 C、 $\frac{3 \sqrt{2} + 1}{3}$ D、 $\frac{9 \sqrt{2} + 3}{19}$

查看试题解析
10. 如图，A，B是反比例函数y＝ $\frac{9}{x}$ （x＞0）图象上的两点，分别过A，B两点向x轴，y轴作垂线段，AD，BE两垂线段交于点G.若图中阴影部分的面积为3，则△OAB的面积为（　　）

A、9 B、10 C、11 D、12

查看试题解析

二、填空题

11. 因式分解： $3 m^{2} - 3$ =

查看试题解析
12. 用配方法求二次函数y＝2x²﹣4x﹣1图象的顶点坐标是.

查看试题解析
13. 已知扇形的半径为6，弧长为2π，则它的圆心角为度.

查看试题解析
14. 如图所示，在两建筑物之间有一高为15米的旗杆，从高建筑物的顶端A点经过旗杆顶点恰好看到矮建筑物的底端墙角C点，且俯角a为60°，又从A点测得矮建筑物左上角顶端D点的俯角β为30°，若旗杆底部点G为BC的中点（点B为点A向地面所作垂线的垂足）则矮建筑物的高CD为.

查看试题解析
15. 如图，已知AB为⊙O的直径，点C，E在⊙O上，且sin∠ACE＝ $\frac{1}{5} \sqrt{5}$ ，点D为弧BE中点，连结DE，则 $\frac{D E^{2}}{A D^{2}}$ 的值为.

查看试题解析
16. 在关于“折纸问题”的数学活动课中，小刚沿菱形纸片ABCD各边中点的连线裁剪得到四边形纸片EFGH，再将纸片EFGH按如图所示分别沿MN、P2折叠，使点E，G落在线段PN上点E，G处，当PNEF时，若阴影部分的周长之和为16，△AEH，△CFG的面积之和为12，则菱形纸片ABCD的一条对角线BD的长为.

查看试题解析

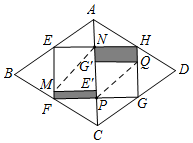
三、解答题

17.

(1)、计算： $\sqrt{12}$ ﹣4sin60°+（2 $\sqrt{2}$ ﹣1）⁰；

(2)、化简：（x+2）²+x（x﹣4）

查看试题解析
18. 如图，在等腰△ABC中，AB＝BC，点D是AC边的中点，延长BD至点E，使得DE＝BD，连结CE.

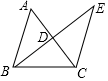(1)、求证：△ABD≌△CED.

(2)、当BC＝5，CD＝3时，求△BCE的周长.

查看试题解析
19. 在如图所示的5×5的方格中，我们把各顶点都在方格格点上的三角形称为格点三角形.如图1是内部只含有1个格点的格点三角形.设每个小正方形的边长为1，完成下列问题：

(1)、在图甲中画一个格点三角形，使它内部只含有2个格点，并写出它的面积.

(2)、在图乙中画一个面积最大的格点三角形，使它的内部只含有A，B，C这3个格点（图乙中已标出），并写出它的面积.

查看试题解析
20. 居民区内的“广场舞”引起媒体关注，小王想了解本小区居民对“广场舞”的看法，进行一次分四个层次的抽样调查（四个层次为：A，非常赞同；B.赞同但要有时间限制；C.无所谓；D.不赞同），并把调查结果绘制成如下两幅不完整的统计图，请根据统计图中的倍息解答下列问题：

(1)、本次被抽查的居民人数是人，将条形统计图补充完整.

(2)、图中∠α的度数是度；该小区有3000名居民，请估计对“广场舞”表示赞同（包括A层次和B层次）的大约有人

(3)、据了解，甲、乙、丙、丁四位居民投不赞同票，小王想从这四位居民中随机选择两位了解具体情况，请用列表或画树状图的方法求出恰好选中甲和乙的概率.

查看试题解析
21. 如图，在△ABC中，AB＝AC，以AB为直径的半圆O交BC于点D，交AC于点E，过点A作半圆O的切线交BC的延长线于点F，连结BE，AD

(1)、求证：∠F＝∠EBC；

(2)、若AE＝2，tan∠EAD＝ $\frac{1}{2}$ ，求AD的长.

查看试题解析
22. 如图，直线y＝2x﹣8分别交x轴、y轴于点A、点B，抛物线y＝ax²+bx（a≠0）经过点A，且顶点Q在直线AB上.

(1)、求a，b的值.

(2)、点P是第四象限内抛物线上的点，连结OP、AP、BP，设点P的横坐标为t，△OAP的面积为s₁ ， △OBP的面积为s₂ ，记s＝s₁+s₂ ，试求s的最值.

查看试题解析
23. 瑞安市曹村镇“八百年灯会”成为温州“申遗”的宝贵项目.某公司生产了一种纪念花灯，每件纪念花灯制造成本为18元.设销售单价x（元），每日销售量y（件）每日的利润w（元）.在试销过程中，每日销售量y（件）、每日的利润w（元）与销售单价x（元）之间存在一定的关系，其几组对应量如下表所示：

（元）

19

20

21

30

（件）

62

60

58

40

(1)、根据表中数据的规律，分别写出毎日销售量y（件），每日的利润w（元）关于销售单价x（元）之间的函数表达式.（利润＝（销售单价﹣成本单价）×销售件数）.

(2)、当销售单价为多少元时，公司每日能够获得最大利润？最大利润是多少？

(3)、根据物价局规定，这种纪念品的销售单价不得高于32元，如果公司要获得每日不低于350元的利润，那么制造这种纪念花灯每日的最低制造成本需要多少元？

查看试题解析
24. 如图，在矩形ABCD中，AB＝6，AD＝3，点E是边CD的中点，点P，Q分别是射线DC与射线EB上的动点，连结PQ，AP，BP，设DP＝t，EQ＝ $\sqrt{2}$ t.

(1)、当点P在线段DE上（不包括端点）时.
①求证：AP＝PQ；

②当AP平分∠DPB时，求△PBQ的面积.

(2)、在点P，Q的运动过程中，是否存在这样的t，使得△PBQ为等腰三角形？若存在，请求出t的值；若不存在，试说明理由.

查看试题解析

成绩 $($ 米 $)$	$1.55$	$1.60$	$1.65$	$1.70$	$1.75$	$1.80$
人数	4	3	5	6	1	1

（元）	19	20	21	30
（件）	62	60	58	40