陕西省西安市雁塔区2019年数学中考一模试卷

试卷更新日期：2019-12-24 类型：中考模拟

进入出卷网下载

一、单选题

1. $\sqrt{3} - 2$ 的绝对值是（）

A、 $2 - \sqrt{3}$ B、 $\sqrt{3} - 2$ C、 $\sqrt{3}$ D、1

查看试题解析
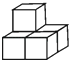
2. 如图，由5个完全相同的小正方体组合成一个立体图形，它的左视图是（）

A、 B、 C、 D、

查看试题解析
3. 下列计算正确的是（）

A、a•a²=a² B、（a²）²=a⁴ C、3a+2a=5a² D、（a²b）³=a²•b³

查看试题解析
4. 如图，将直尺与含30°角的三角尺摆放在一起，若∠1＝20°，则∠2的度数是（）

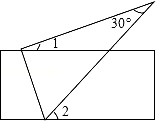A、30° B、40° C、50° D、60°

查看试题解析
5. 已知y关于x成正比例，且当 $x = 2$ 时， $y = - 6$ ，则当 $x = 1$ 时，y的值为 $($ $)$

A、3 B、 $- 3$ C、12 D、 $- 12$

查看试题解析
6. 如图，AD，CE分别是△ABC的中线和角平分线．若AB=AC，∠CAD=20°，则∠ACE的度数是（）

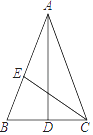A、20° B、35° C、40° D、70°

查看试题解析
7. 在同一平面直角坐标系中,直线=2x+3与y=2x-5的位置关系是（）

A、平行 B、相交 C、重合 D、垂直

查看试题解析
8. 如图，矩形ABCD中，AB＝3，AD＝9，点E在边AD上，AE＝1，过E、D两点的圆的圆心O在边AD的上方，直线BO交AD于点F，作DG⊥BO，垂足为G.当△ABF与△DFG全等时，⊙O的半径为（　　）

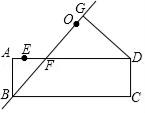A、 $\frac{\sqrt{265}}{2}$ B、 $\frac{\sqrt{265}}{4}$ C、 $\frac{35}{4}$ D、 $\frac{5 \sqrt{15}}{4}$

查看试题解析
9. 如图，AB是⊙O的直径，C是⊙O上一点，OD⊥BC于点D，AC＝4，则OD的长为（　　）

A、1 B、1.5 C、2 D、2.5

查看试题解析
10. 已知抛物线y＝ax²+bx+c（a＜0）经过点（﹣1，0），且满足4a+2b+c＞0，有下列结论：①a+b＞0；②﹣a+b+c＞0；③b²﹣2ac＞5a².其中，正确结论的个数是（　　）

A、0 B、1 C、2 D、3

查看试题解析

二、填空题

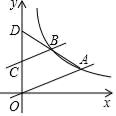
11. 不等式﹣9+3x≤0的非负整数解的和为.

查看试题解析
12. 如果3sinα＝ $\sqrt{3}$ +1，则∠α＝.（精确到0.1度）

查看试题解析
13. 如图，在平面直角坐标系中，直线y＝ $\frac{1}{3}$ x与双曲线y＝ $\frac{k}{x}$ （k≠0）交于点A，过点C（0，2）作AO的平行线交双曲线于点B，连接AB并延长与y轴交于点D（0，4），则k的值为.

查看试题解析

三、解答题

14. 计算： $\sqrt{18}$ +tan60°-（sin45°）^-1-|1- $\sqrt{3}$ |

查看试题解析
15. 计算： $\frac{1}{x} + \frac{x - 2}{x^{2} + x} \div \frac{x^{2} - 4 x + 4}{x + 1}$

查看试题解析
16. 已知：△ABC中，∠A＝36°，AB＝AC，用尺规求作一条过点B的直线，使得截出的一个三角形与△ABC相似.（保留作图痕迹，不写作法）

查看试题解析
17. 某校为了解本校学生每周参加课外辅导班的情况，随机调査了部分学生一周内参加课外辅导班的学科数，并将调查结果绘制成如图1、图2所示的两幅不完整统计图（其中A：0个学科，B：1个学科，C：2个学科，D：3个学科，E：4个学科或以上），请根据统计图中的信息，解答下列问题：

(1)、请将图2的统计图补充完整；

(2)、根据本次调查的数据，每周参加课外辅导班的学科数的众数是个学科；

(3)、若该校共有2000名学生，根据以上调查结果估计该校全体学生一周内参加课外辅导班在3个学科（含3个学科）以上的学生共有人.

查看试题解析
18. 如图，在▱ABCD中，E是对角线BD上的一点，过点C作CF∥DB，且CF＝DE，连接AE，BF，EF．

(1)、求证：△ADE≌△BCF；

(2)、若∠ABE+∠BFC＝180°，则四边形ABFE是什么特殊四边形？说明理由．

查看试题解析
19. 如图，小华在晚上由路灯A走向路灯B.当他走到点P时，发现他身后影子的顶部刚好接触到路灯A的底部；当他向前再步行12m到达点Q时，发现他身前影子的顶部刚好接触到路灯B的底部.已知小华的身高是1.6m，两个路灯的高度都是9.6m，且AP＝QB.

(1)、求两个路灯之间的距离；

(2)、当小华走到路灯B的底部时，他在路灯A下的影长是多少？

查看试题解析
20. 由于雾霾天气频发，市场上防护口罩出现热销，某医药公司每月固定生产甲、乙两种型号的防雾霾口罩共20万只，且所有产品当月全部售出，原料成本、销售单价及工人生产提成如表：

(1)、若该公司五月份的销售收入为300万元，求甲、乙两种型号的产品分别是多少万只？

(2)、公司实行计件工资制，即工人每生产一只口罩获得一定金额的提成，如果公司六月份投入总成本（原料总成本+生产提成总额）不超过239万元，应怎样安排甲、乙两种型号的产量，可使该月公司所获利润最大？并求出最大利润（利润=销售收入﹣投入总成本）

查看试题解析
21. 汤姆斯杯世界男子羽毛球团体赛小组赛比赛规则：两队之间进行五局比赛，其中三局单打，两局双打，五局比赛必须全部打完，赢得三局及以上的队获胜.假如甲，乙两队每局获胜的机会相同.

(1)、若前四局双方战成2：2，那么甲队最终获胜的概率是；

(2)、现甲队在前两周比赛中已取得2：0的领先，那么甲队最终获胜的概率是多少？

查看试题解析
22. 如图，AB是⊙O的直径，直线AT切⊙O于点A，BT交⊙O于C，已知∠B＝30°，AT＝ $\sqrt{3}$ ，求⊙O的直径AB和弦BC的长.

查看试题解析
23. 抛物线y=﹣x²+bx+c经过点A、B、C，已知A（﹣1，0），C（0，3）.

(1)、求抛物线的解析式；

(2)、如图1，P为线段BC上一点，过点P作y轴平行线，交抛物线于点D，当△BDC的面积最大时，求点P的坐标；

(3)、如图2，抛物线顶点为E，EF⊥x轴于F点，M（m，0）是x轴上一动点，N是线段EF上一点，若∠MNC=90°，请指出实数m的变化范围，并说明理由.

查看试题解析
24. 如图，△BCD内接于⊙O，直径AB经过弦CD的中点M，AE交BC的延长线于点E，连接AC，∠EAC＝∠ABD＝30°．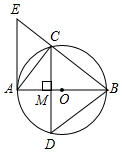

(1)、求证：△BCD是等边三角形；

(2)、求证：AE是⊙O的切线；

(3)、若CE＝2，求⊙O的半径．

查看试题解析