陕西省西安市莲湖区2019届九年级数学中考模拟试卷（一）

试卷更新日期：2019-12-24 类型：中考模拟

进入出卷网下载

一、单选题

1. $\sqrt{3}$ -2的绝对值是（）

A、 $2 - \sqrt{3}$ B、 $\sqrt{3} - 2$ C、 $\sqrt{3}$ D、1

查看试题解析
2. 如图是由若干个大小相同的小正方体堆砌而成的几何体，那么其三种视图中面积最小的是（）

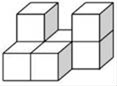A、主视图 B、俯视图 C、左视图 D、一样大

查看试题解析
3. 正比例函数 $y = k x$ 的自变量取值增加2，函数值就相应减少2，则 $k$ 的值为（）

A、2 B、-2 C、-1 D、4

查看试题解析
4. 如图，将直尺与含30°角的三角尺摆放在一起，若∠1＝20°，则∠2的度数是（）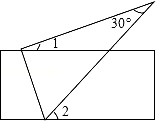

A、30° B、40° C、50° D、60°

查看试题解析
5. 计算（1+ $\frac{1}{x}$ ）÷ $\frac{x^{2} + 2 x + 1}{x}$ 的结果是（）

A、x+1 B、 $\frac{1}{x + 1}$ C、 $\frac{x}{x + 1}$ D、 $\frac{x + 1}{x}$

查看试题解析
6. 在△ABC中，∠BAC＝115°，DE、FG分别为AB、AC的垂直平分线，则∠EAG的度数为（　　）

A、50° B、40° C、30° D、25°

查看试题解析
7. 已知一次函数y＝(m－4)x＋2m＋1的图象不经过第三象限，则m的取值范围是（）

A、m＜4 B、 $- \frac{1}{2}$ ≤m＜4 C、 $- \frac{1}{2}$ ≤m≤4 D、m≤ $- \frac{1}{2}$

查看试题解析
8.
填在下面各正方形中的四个数之间都有相同的规律，根据这种规律，m的值应是（　　）

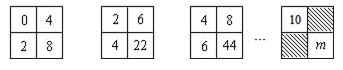A、110 B、158 C、168 D、178

查看试题解析
9. 如图，直径为10的⊙A经过点C(0，5)和点0(0，0)，B是y轴右侧⊙A优弧上一点，则∠OBC的余弦值为（）

A、 $\frac{1}{2}$ B、 $\frac{3}{4}$ C、 $\frac{\sqrt{3}}{2}$ D、 $\frac{4}{5}$

查看试题解析
10. 在同一平面直角坐标系中,直线=2x+3与y=2x-5的位置关系是（）

A、平行 B、相交 C、重合 D、垂直

查看试题解析
11. 已知二次函数y=（x﹣1）²﹣4，当y＜0时，x的取值范围是（　　）

A、﹣3＜x＜1 B、x＜﹣1或x＞3 C、﹣1＜x＜3 D、x＜﹣3或x＞1

查看试题解析
12. 如图，函数y=ax²+bx+c的图象过点（﹣1，0）和（m，0），请思考下列判断：①abc＜0；②4a+c＜2b；③ $\frac{b}{c}$ =1﹣ $\frac{1}{m}$ ；④am²+（2a+b）m+a+b+c＜0；⑤|am+a|= $\sqrt{b^{2} - 4 a c}$ 正确的是（　　）

A、①③⑤ B、①②③④⑤ C、①③④ D、①②③⑤

查看试题解析

二、填空题

13. 不等式﹣9+3x≤0的非负整数解的和为.

查看试题解析
14. 分解因式：m²n﹣4mn﹣4n＝．

查看试题解析
15. 如图，正五边形 $ABCDE$ 内接于 $⊙ O$ ，若 $⊙ O$ 的半径为 $5$ ，则弧 $AB$ 的长为.

查看试题解析
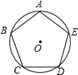16. 如图，在平面直角坐标系中，直线y＝ $\frac{1}{3}$ x与双曲线y＝ $\frac{k}{x}$ （k≠0）交于点A，过点C（0，2）作AO的平行线交双曲线于点B，连接AB并延长与y轴交于点D（0，4），则k的值为.

查看试题解析
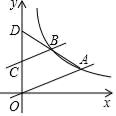17. 如图，在边长为1的正方形ABCD的各边上，截取AE＝BF＝CG＝DH＝x，连接AF、BG、CH、DE构成四边形PQRS.用x的代数式表示四边形PQRS的面积S.则S＝.

查看试题解析

三、解答题

18. 如图，已知PA、PB是⊙O的切线，A、B分别为切点，∠OAB=30°.

(1)、∠APB=；

(2)、当OA=2时，AP=.

查看试题解析
19. 计算：

(1)、| $\sqrt{2}$ ﹣1|+（3.14﹣π）⁰+ ${(\frac{1}{2})}^{- 1}$ + $\sqrt[3]{- 8}$ .

(2)、 $\frac{1}{x}$ + $\frac{x - 2}{x^{2} + x}$ ÷ $\frac{x^{2} - 4 x + 4}{x + 1}$

查看试题解析
20. 解方程： $\frac{1}{x + 2} + \frac{4 x}{x^{2} - 4} - \frac{2}{x - 2} = 1$ ．

查看试题解析
21. 尺规作图（只保留作图痕迹，不要求写出作法）.如图，已知∠α和线段a，求作△ABC，使∠A=∠α，∠C=90°，AB=a.

查看试题解析
22. 为了解学生参加户外活动的情况，某中学对学生参加户外活动的时间进行抽样调查，并将调查结果绘制成如图两幅不完整的统计图，根据图示，请回答下列问题：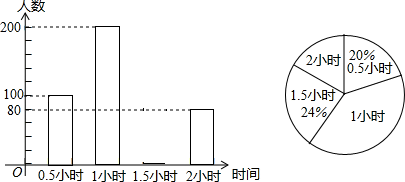

(1)、求户外活动时间为1.5小时的学生有多少人？并补全条形统计图

(2)、每天户外活动时间的中位数是小时？

(3)、该校共有1800名学生，请估计该校每天户外活动超过1小时的学生人数有多少人？

查看试题解析
23. 如图，在四边形 $A B C D$ 中， $A D$ ∥ $B C$ ， $A E ⊥ A D$ 交 $B D$ 于点 $E$ ， $C F ⊥ B C$ 交 $B D$ 于点 $F$ ，且 $A E = C F$ ；求证：四边形 $A B C D$ 是平行四边形.

查看试题解析
24. 如图，小华在晚上由路灯A走向路灯B.当他走到点P时，发现他身后影子的顶部刚好接触到路灯A的底部；当他向前再步行12m到达点Q时，发现他身前影子的顶部刚好接触到路灯B的底部.已知小华的身高是1.6m，两个路灯的高度都是9.6m，且AP＝QB.

(1)、求两个路灯之间的距离；

(2)、当小华走到路灯B的底部时，他在路灯A下的影长是多少？

查看试题解析
25. 在一条笔直的公路上依次有A，C，B三地，甲、乙两人同时出发，甲从A地骑自行车去B地，途经C地休息1分钟，继续按原速骑行至B地，甲到达B地后，立即按原路原速返回A地；乙步行从B地前往A地．甲、乙两人距A地的路程y（米）与时间x（分）之间的函数关系如图所示，请结合图象解答下列问题：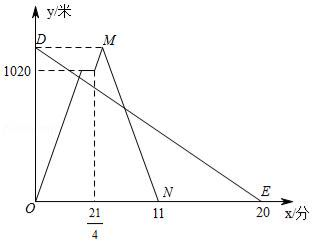

(1)、请写出甲的骑行速度为米/分，点M的坐标为；

(2)、求甲返回时距A地的路程y与时间x之间的函数关系式（不需要写出自变量的取值范围）；

(3)、请直接写出两人出发后，在甲返回A地之前，经过多长时间两人距C地的路程相等．

查看试题解析
26. 如图，AB是⊙O的直径，直线AT切⊙O于点A，BT交⊙O于C，已知∠B＝30°，AT＝ $\sqrt{3}$ ，求⊙O的直径AB和弦BC的长.

查看试题解析
27. 在平面直角坐标系xOy中，抛物线y＝ax²+bx+c经过点A，B，C，已知A(﹣1，0)，B(5，0)，C(0，5)

(1)、求抛物线与直线BC的表达式；

(2)、如图1，P为线段BC上一点，过点P作y轴平行线，交抛物线于点D，当△BCD的面积最大时，求点P的坐标；

(3)、如图2，抛物线顶点为E，EF⊥x轴于点F，N是线段EF上一动点，M(m，0)是x轴上一动点，若∠MNC＝90°，直接写出实数m的取值范围.

查看试题解析
28. 已知：如图，在梯形ABCD中，AB∥CD，∠D＝90°，AD＝CD＝2，点E在边AD上（不与点A、D重合），∠CEB＝45°，EB与对角线AC相交于点F，设DE＝x.

(1)、用含x的代数式表示线段CF的长；

(2)、如果把△CAE的周长记作C_△_CAE ， △BAF的周长记作C_△_BAF ，设 $\frac{C_{Δ C A E}}{C_{Δ B A F}}$ ＝y，求y关于x的函数关系式，并写出它的定义域；

(3)、当∠ABE的正切值是 $\frac{3}{5}$ 时，求AB的长.

查看试题解析