陕西省宝鸡市四中2019届九年级数学中考模拟试卷(5月)
试卷更新日期:2019-12-24 类型:中考模拟
一、单选题
-
1. 5的相反数是( )A、 B、5 C、 D、﹣52. 港珠澳大桥是中国境内一座连接着香港、珠海和澳门的桥隧工程,工程投资总额1269亿元,1269亿用科学记数法表示为( )A、1.269×1010 B、1.269×1011 C、12.69×1010 D、0.1269×10123. 等腰三角形两边长分别是2 cm和5 cm,则这个三角形周长是( )A、9 cm B、12 cm C、9 cm或12 cm D、14 cm4. 已知一次函数的图象过点(0,3)和(﹣2,0),那么直线必过下面的点( )A、(4,6) B、(﹣4,﹣3) C、(6,9) D、(﹣6,6)5. 如图△ABC中,AC的垂直平分线分别交AC,AB于点D,F,BE⊥DF交DF的延长线于点E,已知∠A=30°,BC=2,AF=BF,则四边形BCDE的面积是( )
 A、2 B、3 C、4 D、46. 关于x的一元二次方程(a﹣1)x2+x+a2﹣1=0的一个根0,则a值为( )A、1 B、﹣1 C、±1 D、07. 如图,AB是⊙O的直径,△ACD内接于⊙O,延长AB,CD相交于点E,若∠CAD=35°,∠CDA=40°,则∠E的度数是( )
A、2 B、3 C、4 D、46. 关于x的一元二次方程(a﹣1)x2+x+a2﹣1=0的一个根0,则a值为( )A、1 B、﹣1 C、±1 D、07. 如图,AB是⊙O的直径,△ACD内接于⊙O,延长AB,CD相交于点E,若∠CAD=35°,∠CDA=40°,则∠E的度数是( ) A、20° B、25° C、30° D、35°8. 如图,菱形ABCD的周长是20,对角线AC,BD相交于点O,若BD=6,则菱形ABCD的面积是( )
A、20° B、25° C、30° D、35°8. 如图,菱形ABCD的周长是20,对角线AC,BD相交于点O,若BD=6,则菱形ABCD的面积是( )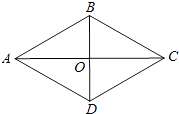 A、6 B、12 C、24 D、489. 二次函数y=ax2+bx+c(a≠0)的部分图象如图,图象过点(-1,0),对称轴为直线x=2,下列结论:①4a+b=0;②9a+c>3b;③8a+7b+2c>0;④当x>-1时,y的值随x值的增大而增大.其中正确的结论有( )
A、6 B、12 C、24 D、489. 二次函数y=ax2+bx+c(a≠0)的部分图象如图,图象过点(-1,0),对称轴为直线x=2,下列结论:①4a+b=0;②9a+c>3b;③8a+7b+2c>0;④当x>-1时,y的值随x值的增大而增大.其中正确的结论有( ) A、1个 B、2个 C、3个 D、4个10.
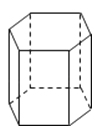
A、1个 B、2个 C、3个 D、4个10.如图,下列选项中不是正六棱柱三视图的是( )
 A、
A、 B、
B、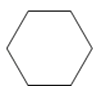 C、
C、 D、
D、
二、填空题
-
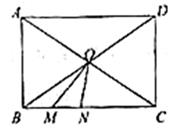
11. 分解因式:4m2﹣16n2= .12. 若顺次连接四边形ABCD各边中点所得四边形为矩形,则四边形ABCD的对角线AC、BD之间的关系为.13. 点A(3,﹣2)关于y轴的对称点B在反比例函数y= 的图象上,则B点的坐标为;k=.14. 如图, 为矩形 对角线 , 的交点,AB=6,M,N是直线BC上的动点,且 ,则 的最小值是.
 15. 如图,某飞机于空中探测某座山的高度,在点 处飞机的飞行高度是 米,从飞机上观测山顶目标 的俯角是 ,飞机继续以相同的高度飞行 米到 地,此时观察目标 的俯角是 ,则这座山的高度 是米(参考数据: , , )
15. 如图,某飞机于空中探测某座山的高度,在点 处飞机的飞行高度是 米,从飞机上观测山顶目标 的俯角是 ,飞机继续以相同的高度飞行 米到 地,此时观察目标 的俯角是 ,则这座山的高度 是米(参考数据: , , )
三、解答题
-
16. 计算:﹣24﹣ +|1﹣4sin60°|+(2015π)0.17. 解分式方程:18. 作图:如图已知△ABC.
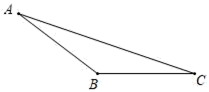 (1)、①作出点A到直线BC的垂线段AD;
(1)、①作出点A到直线BC的垂线段AD;②作出点B到直线AC的垂线段BE;
(2)、已知BC=6,AD=4,AC=8那么2BE=.19. 如图,∠AEF=∠AFE,AC=AD,CE=DF,求证:∠C=∠D. 20. 为了解本校九年级学生期末数学考试情况,在九年级随机抽取了一部分学生 的期末数学成绩为样本,分为 A(90~100 分);B(80~89 分);C(60~79 分);D(0~59 分)四个等级进行统计,并将统计结果绘制成如下统计图,请你根据统计图解答以下 问题.
20. 为了解本校九年级学生期末数学考试情况,在九年级随机抽取了一部分学生 的期末数学成绩为样本,分为 A(90~100 分);B(80~89 分);C(60~79 分);D(0~59 分)四个等级进行统计,并将统计结果绘制成如下统计图,请你根据统计图解答以下 问题.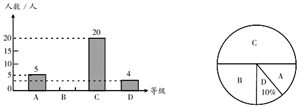 (1)、这次随机抽取的学生共有多少人?(2)、请补全条形统计图;(3)、这个学校九年级共有学生 1200 人,若分数为 80 分(含 80 分)以上为优秀,请估 计这次九年级学生期末数学考试成绩为优秀的学生人数大约有多少?21. 甲、乙两人相约周末登花果山,甲、乙两人距地面的高度y(米)与登山时间x(分)之间的函数图象如图所示,根据图象所提供的信息解答下列问题:
(1)、这次随机抽取的学生共有多少人?(2)、请补全条形统计图;(3)、这个学校九年级共有学生 1200 人,若分数为 80 分(含 80 分)以上为优秀,请估 计这次九年级学生期末数学考试成绩为优秀的学生人数大约有多少?21. 甲、乙两人相约周末登花果山,甲、乙两人距地面的高度y(米)与登山时间x(分)之间的函数图象如图所示,根据图象所提供的信息解答下列问题: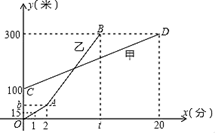 (1)、甲登山上升的速度是每分钟米,乙在A地时距地面的高度b为米;(2)、若乙提速后,乙的登山上升速度是甲登山上升速度的3倍,请求出乙登山全程中,距地面的高度y(米)与登山时间x(分)之间的函数关系式;(3)、登山多长时间时,甲、乙两人距地面的高度差为70米?22. 新年游园会中有一款电子飞镖的游戏. 如图, 靶被等分成2个区域,分别涂上红色和蓝色, 靶被等分成3个区域,分别涂上红色、蓝色、和白色. 小彬向 靶、小颖向 靶分别投掷一枚电子飞镖,飞镖随机落在靶盘的某一位置,若两枚飞镖命中部分的颜色恰好配成紫色,小彬获得奖品,否则,小颖获得奖品(若飞镖落在边界线上时,重投一次,直到落在某一区域).这个游戏公平吗?说明理由.
(1)、甲登山上升的速度是每分钟米,乙在A地时距地面的高度b为米;(2)、若乙提速后,乙的登山上升速度是甲登山上升速度的3倍,请求出乙登山全程中,距地面的高度y(米)与登山时间x(分)之间的函数关系式;(3)、登山多长时间时,甲、乙两人距地面的高度差为70米?22. 新年游园会中有一款电子飞镖的游戏. 如图, 靶被等分成2个区域,分别涂上红色和蓝色, 靶被等分成3个区域,分别涂上红色、蓝色、和白色. 小彬向 靶、小颖向 靶分别投掷一枚电子飞镖,飞镖随机落在靶盘的某一位置,若两枚飞镖命中部分的颜色恰好配成紫色,小彬获得奖品,否则,小颖获得奖品(若飞镖落在边界线上时,重投一次,直到落在某一区域).这个游戏公平吗?说明理由. 23. 如图,在△ABC中,AB=AC,以AB为直径作⊙O交BC于点D.过点D作EF⊥AC,垂足为E,且交AB的延长线于点F.
23. 如图,在△ABC中,AB=AC,以AB为直径作⊙O交BC于点D.过点D作EF⊥AC,垂足为E,且交AB的延长线于点F. (1)、求证:EF是⊙O的切线;(2)、若AB=8,∠A=60°,求BD的长.24. 如图,已知直线 与抛物线 相交于A,B两点,且点A(1,-4)为抛物线的顶点,点B在x轴上。
(1)、求证:EF是⊙O的切线;(2)、若AB=8,∠A=60°,求BD的长.24. 如图,已知直线 与抛物线 相交于A,B两点,且点A(1,-4)为抛物线的顶点,点B在x轴上。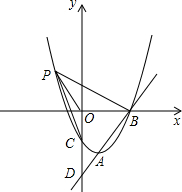 (1)、求抛物线的解析式;(2)、在(1)中抛物线的第二象限图象上是否存在一点P,使△POB与△POC全等?若存在,求出点P的坐标;若不存在,请说明理由;(3)、若点Q是y轴上一点,且△ABQ为直角三角形,求点Q的坐标。25. 如图,在平面直角坐标系中,四边形OABC为菱形,点C的坐标为(4,0),∠AOC=60°,垂直于x轴的直线l从y轴出发,沿x轴正方向以每秒1个单位长度的速度运动,设直线l与菱形OABC的两边分别交于点M、N(点M在点N的上方).
(1)、求抛物线的解析式;(2)、在(1)中抛物线的第二象限图象上是否存在一点P,使△POB与△POC全等?若存在,求出点P的坐标;若不存在,请说明理由;(3)、若点Q是y轴上一点,且△ABQ为直角三角形,求点Q的坐标。25. 如图,在平面直角坐标系中,四边形OABC为菱形,点C的坐标为(4,0),∠AOC=60°,垂直于x轴的直线l从y轴出发,沿x轴正方向以每秒1个单位长度的速度运动,设直线l与菱形OABC的两边分别交于点M、N(点M在点N的上方).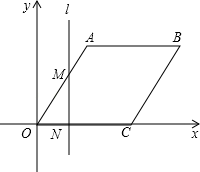 (1)、求A、B两点的坐标;(2)、设△OMN的面积为S , 直线l运动时间为t秒(0≤t≤6),试求S与t的函数表达式;(3)、在题(2)的条件下,是否存在某一时刻,使得△OMN的面积与OABC的面积之比为3:4?如果存在,请求出t的取值;如果不存在,请说明理由.
(1)、求A、B两点的坐标;(2)、设△OMN的面积为S , 直线l运动时间为t秒(0≤t≤6),试求S与t的函数表达式;(3)、在题(2)的条件下,是否存在某一时刻,使得△OMN的面积与OABC的面积之比为3:4?如果存在,请求出t的取值;如果不存在,请说明理由.