陕西省宝鸡市岐山县2019届九年级数学中考一模试卷

试卷更新日期：2019-12-24 类型：中考模拟

进入出卷网下载

一、单选题

1. $- \frac{2}{3}$ 的倒数是（　　）

A、 $- \frac{3}{2}$ B、 $\frac{3}{2}$ C、 $\frac{2}{3}$ D、 $- \frac{2}{3}$

查看试题解析
2.
如图是某几何体的三视图，该几何体是（　　）

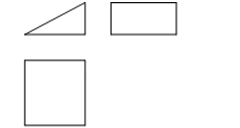A、三棱柱 B、三棱锥 C、长方体 D、正方体

查看试题解析
3. 将一副三角板按如图所示摆放，DE∥BC，点D在线段AC上，点F在线段BC上，则∠AGF的度数为（　　）

A、 $60^{\circ}$ B、 $70^{\circ}$ C、 $75^{\circ}$ D、 $80^{\circ}$

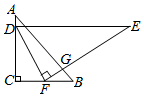查看试题解析
4. 直线y=2x关于x轴对称的直线是（　　）

A、 $y = \frac{1}{2} x$ B、 $y = - \frac{1}{2} x$ C、 $y = 2 x$ D、 $y = - 2 x$

查看试题解析
5. 下列运算正确的是（　　）

A、 $a^{2} + a^{3} = a^{2}$ B、 ${(- a^{3})}^{2} = a^{6}$ C、 ${(a - b)}^{2} = a^{2} - b^{2}$ D、 ${(- 2 a^{3})}^{2} = - 4 a^{6}$

查看试题解析
6. 如图，在等腰△ABC中，∠A=120°，AB=4，则△ABC的面积为（　　）

A、 $2 \sqrt{3}$ B、4 C、 $4 \sqrt{3}$ D、 $8 \sqrt{3}$

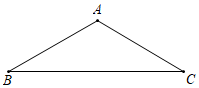查看试题解析
7. 已知点A（a，b）是一次函数y=-x+4和反比例函数y= $\frac{1}{x}$ 的一个交点，则代数式a²+b²的值为（　　）

A、8 B、10 C、12 D、14

查看试题解析
8. 如图，在菱形ABCD中，两对角线AC、BD交于点O，AC=8，BD=6，当△OPD是以PD为底的等腰三角形时，CP的长为（　　）

A、2 B、 $\frac{18}{5}$ C、 $\frac{7}{5}$ D、 $\frac{5}{2}$

查看试题解析
9. 如图，半径为3的⊙O经过等边△ABO的顶点A，B，点P为半径OB上的动点，连接AP，过点P作PC⊥AP交⊙O于点C，当∠ACP=30°时，AP的长为（　　）

A、3 B、3或 $\frac{3 \sqrt{3}}{2}$ C、 $1.5$ D、3或 $1.5$

查看试题解析
10. 将抛物线C：y=x²-2mx向右平移5个单位后得到抛物线C′，若抛物线C与C′关于直线x=-1对称，则m的值为（　　）

A、 $- 7$ B、7 C、 $\frac{7}{2}$ D、 $- \frac{7}{2}$

查看试题解析

二、填空题

11. 分解因式：a-2a²+a³=.

查看试题解析
12. 如图，AC、AD是正五边形的对角线，则∠CAD的度数是.

查看试题解析
13. 如图，A、B两点在双曲线y= $\frac{4}{x}$ 上，分别过A、B两点向坐标轴作垂线，已知S₁+S₂=6，则S_阴影=.

查看试题解析
14. 如图，在矩形ABCD中，AB=4，AD=6，E是AB边的中点，F是线段BC边上的动点，将△EBF沿EF所在直线折叠得到△EB′F，连接B′D，则B′D的最小值是.

查看试题解析

三、解答题

15. 计算： $\sqrt{18}$ -（π-1）⁰-2cos45°+（ $\frac{1}{2}$ ）^-².

查看试题解析
16. 某市为了鼓励居民节约用水，采用分段计费的方法按月计算每户家庭的水费，月用水量不超过20 $m^{3}$ 时，按2元／ $m^{3}$ 计费；月用水量超过20 $m^{3}$ 时，其中的20 $m^{3}$ 仍按2元／ $m^{3}$ 收费，超过部分按 $2.6$ 元／ $m^{3}$ 计费.设每户家庭用用水量为 $x m^{3}$ 时，应交水费 $y$ 元.

(1)、分别求出 $0 \leq x \leq 20$ 和 $x > 20$ 时 $y$ 与 $x$ 的函数表达式；

(2)、小明家第二季度交纳水费的情况如下：

月份

四月份

五月份

六月份

交费金额

30元

34元

42.6元

小明家这个季度共用水多少立方米？

查看试题解析
17. 如图，四边形ABCD是⊙O的内接四边形，AC为直径， $\overset{}{B D}$ = $\overset{}{A D}$ ，DE⊥BC，垂足为E.

(1)、求证：CD平分∠ACE；

(2)、判断直线ED与⊙O的位置关系，并说明理由；

(3)、若CE=1，AC=4，求阴影部分的面积.

查看试题解析
18. 解分式方程： $\frac{x - 3}{x - 2} - 1 = \frac{x}{3}$

查看试题解析
19. 如图，已知△ABC中，D为AB的中点，请在边AC作点E，使得DE= $\frac{1}{2}$ BC（保留作图痕迹，不要求写作法）

查看试题解析
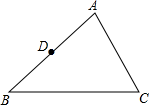20. 如图，四边形ABCD是菱形，CE⊥AB交AB的延长线于点E，CF⊥AD交AD的延长线于点F，求证：DF=BE．

查看试题解析
21. 中学生上网现象越来越受到社会的关注，小记者小慧随机调查了某校若干学生和家长对上网现象的看法制作了如下的统计图1和2.请根据相关信息，解答或补全下列问题.

(1)、补全图1；

(2)、求图2中表示家长“赞成”的圆心角的度数；

(3)、该校共有1600名学生，请你估计这所中学的所有学生中，对上网持“反对”态度的有多少名？

查看试题解析
22. 如图，河流的两岸PQ、MN互相平行，河岸PQ上有一排小树，已知相邻两树之间的距离CD=50米，某人在河岸MN的A处测得∠DAN=35°，然后沿河岸走了120米到达B处，测得∠CBN=70°.求河流的宽度CE（结果保留两个有效数字）.（参考数据：sin35°≈0.57，cos35°≈0.82，tan35°≈0.70，sin70°≈0.94，cos70°≈0.34，tan70°≈2.75）

查看试题解析
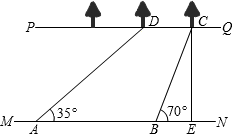23. 甲、乙、丙3人聚会，每人带了一件礼物，3件礼物从外盒包装看完全相同，里面的东西只有颜色不同，将3件礼物放在一起.

(1)、甲从中随机抽取一件，求甲抽到不是自己带来的礼物的概率；

(2)、每人从中随机抽取一件，求甲、乙、丙3人抽到的都不是自己带来的礼物的概率.

查看试题解析
24. 如图在平面直角坐标系中抛物线经过A（2，0），B（0，4）两点，将△OAB绕点O逆时针旋转90°得到△OCD，点D在抛物线上.

(1)、求该抛物线的表达式；

(2)、已知点M在y轴上（点M不与点B重合），连接AM，若△AOM与△AOB相似，试求点M的坐标.

查看试题解析
25. 问题探究：

(1)、已知：如图①，△ABC中请你用尺规在BC边上找一点D，使得点A到点BC的距离最短.

(2)、托勒密（Ptolemy）定理指出，圆的内接四边形两对对边乘积的和等于两条对角线的乘积.如图②，P是正△ABC外接圆的劣弧BC上任一点（不与B、C重合），请你根据托勒密（Ptolemy）定理证明：PA=PB+PC

(3)、如图③，某学校有一块两直角边长分别为30m、60m的直角三角形的草坪，现准备在草坪内放置一对石凳及垃圾箱在点P处，使P到A、B、C三点的距离之和最小，那么是否存在符合条件的点P？若存在，请作出点P的位置，并求出这个最短距离（结果保留根号）；若不存在，请说明理由.

查看试题解析

月份	四月份	五月份	六月份
交费金额	30元	34元	42.6元