陕西省宝鸡市岐山县2019届九年级数学中考二模试卷

试卷更新日期：2019-12-24 类型：中考模拟

进入出卷网下载

一、单选题

1. 相反数等于﹣2的数是（　　）

A、2 B、﹣2 C、 $\frac{1}{2}$ D、±2

查看试题解析
2. 如图是由5个相同的小正方体组成的立体图形，它的左视图是（）

A、 B、 C、 D、

查看试题解析
3. 将一副三角板如图放置，使点A在DE上，BC∥DE，则∠AFC的度数是（　　）

A、45° B、50° C、60° D、75°

查看试题解析
4. 若正比例函数y=kx的图象经过点A（k，9），且经过第一、三象限，则k的值是（）

A、﹣9 B、﹣3 C、3 D、﹣3或3

查看试题解析
5. 下列运算：①a²•a³＝a⁶；②（a³）²＝a⁶；③a⁵÷a⁵＝a；④2a²bc﹣a²bc＝a²bc.其中正确的个数是（　　）

A、2个 B、3个 C、4个 D、1个

查看试题解析
6. 如图，在平行四边形ABCD中，AC、BD相交于点O，点E是OA的中点，连接BE并延长交AD于点F，已知S_△_AEF＝3，则下列结论：① $\frac{A F}{F D} = \frac{1}{2}$ ；②S_△_BCE＝30；③S_△_ABE＝9；④△AEF∽△ACD，其中一定正确的是（　　）

A、①②③④ B、①③ C、②③④ D、①②③

查看试题解析
7. 如图，一次函数y₁＝k₁x+b₁与反比例函数 $y_{2} = \frac{k_{2}}{x}$ 的图象交于点A（1，3），B（3，1）两点，若y₁＜y₂ ，则x的取值范围是（　　）

A、x＜1 B、x＜3 C、0＜x＜3 D、x＞3或0＜x＜1

查看试题解析
8. 如图，在△ABC中，AB＝AC，点D、E分别是边AB，AC的中点，点G，F在BC边上，四边形DGFE是正方形.若DE＝4cm，则AC的长为（　　）

A、4cm B、2 $\sqrt{5}$ cm C、8cm D、4 $\sqrt{5}$ cm

查看试题解析
9. 如图，点A、B、C、D在⊙O上， $\overset{⌢}{C B} = \overset{⌢}{C D}$ ，∠CAD＝30°，∠ACD＝50°，则∠ADB＝（　　）

A、30° B、50° C、70° D、80°

查看试题解析
10. 若二次函数y=ax²+bx+c（a＜0）的图象经过点（2，0），且其对称轴为x=﹣1，则使函数值y＞0成立的x的取值范围是（）

A、x＜﹣4或x＞2 B、﹣4≤x≤2 C、x≤﹣4或x≥2 D、﹣4＜x＜2

查看试题解析

二、填空题

11. 实数a，b，c在数轴上对应点的位置如图所示，则bca（填“＞”“＜”或“＝”）

查看试题解析
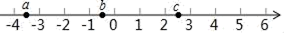12. 正多边形的中心角与该正多边形的一个内角的关系是.

查看试题解析
13. 如图，在平面直角坐标系中，△ABC的顶点A和C分别在x轴、y轴的正半轴上，且AB∥y轴，AB＝4，△ABC的面积为2，将△ABC以点B为旋转中心，顺时针旋转90°得到△DBE，一反比例函数图象恰好过点D时，则此反比例函数解析式是.

查看试题解析
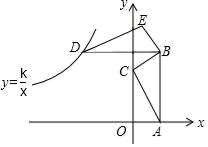14. 如图，∠AOB＝60°，点P是∠AOB内一定点，且OP＝2，若点M、N分别是射线OA、OB上异于点O的动点，则△PMN周长的最小值是.

查看试题解析

三、解答题

15. 计算： ${(\sqrt{2} - π)}^{0} + {(\frac{1}{2})}^{- 2} - \sqrt{9} + \sqrt[3]{- 27}$ .

查看试题解析
16. 解分式方程： $\frac{x}{2 - x} = 4 - \frac{7}{x - 2}$ .

查看试题解析
17. 如图，已知∠ABC，射线BC上有一点D.

求作：以BD为底边的等腰△MBD，点M在∠ABC内部，且到∠ABC两边的距离相等.

查看试题解析
18. 已知：如图，AB＝AD，AC＝AE，∠BAG＝∠DAF.

求证：BC＝DE.

查看试题解析
19. 某中学为了帮助贫困学生读书，由校团委向全校2400名学生发起了“脱贫攻坚我在行”爱心捐款活动，为了解捐款情况，校团委随机调查了部分学生的捐款金额，并用得到的数据绘制了如下统计图1和图2，请根据相关信息，解答下列问题：

(1)、本次接受随机调查的学生人数为，图①中m的值是；

(2)、请补全条形统计图；

(3)、求本次调查获取的样本数据的众数和中位数；

(4)、根据样本数据，估计该校本次活动捐款金额为10元的学生人数.

查看试题解析
20. 2018年，广州国际龙舟邀请赛于6月23日在中山大学北门广场至广州大桥之间的珠江河段举行.上午8时，参赛龙舟同时出发，甲、乙两队在比赛中，路程y（千米）与时间x（小时）的函数关系如图所示，甲队在上午11时30分到达终点.

(1)、在比赛过程中，乙队何时追上甲队？

(2)、在比赛过程中，甲、乙两队何时相距最远？

查看试题解析
21. 某校组织一项公益知识竞赛，比赛规定：每个代表队由3名男生、4名女生和1名指导老师组成.但参赛时，每个代表队只能有3名队员上场参赛，指导老师必须参加，另外2名队员分别在3名男生和4名女生中各随机抽出一名.七年级（1）班代表队有甲、乙、丙三名男生和A、B、C、D4名女生及1名指导老师组成.求：

(1)、抽到D上场参赛的概率；

(2)、恰好抽到由男生丙、女生C和这位指导老师一起上场参赛的概率.（请用“画树状图”或“列表”的方式给出分析过程）

查看试题解析
22. 如图，PA、PB是⊙O的切线，A、B为切点，连接AO并延长，交PB的延长线于点C，连接PO，交⊙O于点D.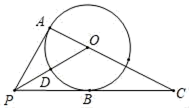

(1)、求证：∠APO＝∠CPO；

(2)、若⊙O的半径为3，OP＝6，∠C＝30°，求PC的长.

查看试题解析
23. 如图，已知直线y＝﹣2x+4分别交x轴、y轴于点A、B.抛物线过A、B两点，点P是线段AB上一动点，过点P作PC⊥x轴于点C，交抛物线于点D.

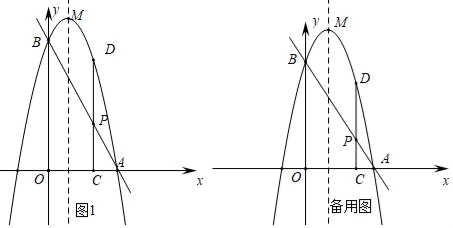(1)、如图1，设抛物线顶点为M，且M的坐标是（ $\frac{1}{2}$ ， $16 = a^{2} + b^{2} - 2 a b \cos \frac{π}{6}$ ），对称轴交AB于点N.
①求抛物线的解析式；

②是否存在点P，使四边形MNPD为菱形？并说明理由；

(2)、是否存在这样的点D，使得四边形BOAD的面积最大？若存在，求出此时点D的坐标；若不存在，请说明理由.

查看试题解析
24.

(1)、问题发现

如图1，△ACB和△DCE均为等边三角形，点A、D、E在同一条直线上，连接BE.

填空：

①∠AEB的度数为；

②线段AD、BE之间的数量关系为.

(2)、拓展研究
如图2，△ACB和△DCE均为等腰直角三角形，∠ACB＝∠DCE＝90°，点A、D、E在同一条直线上，CM为△DCE中DE边上的高，连接BE，请判断∠AEB的度数及线段CM、AE、BE之间的数量关系，并说明理由.

(3)、解决问题
如图3，在正方形ABCD中，CD＝2 $\sqrt{2}$ ，若点P满足PD＝2，且∠BPD＝90°，请直接写出点A到BP的距离.

查看试题解析