陕西省宝鸡市凤翔县2019年九年级数学中考一模试卷

试卷更新日期：2019-12-24 类型：中考模拟

进入出卷网下载

一、单选题

1. $\frac{1}{4}$ 的算术平方根是（）

A、 $\frac{1}{2}$ B、 $- \frac{1}{2}$ C、 $\frac{1}{16}$ D、 $\pm \frac{1}{2}$

查看试题解析
2. 下列立体图形中，侧面展开图是扇形的是（）

A、 B、 C、 D、

查看试题解析
3. 如图，直线l₁∥l₂ ，且分别与直线l交于C，D两点，把一块含30°角的三角尺按如图所示的位置摆放.若∠1=52°，则∠2的度数为（）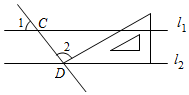

A、92° B、98° C、102° D、108°

查看试题解析
4. 正比例函数y＝kx的图象如图所示，则k的值为（）

A、 $- \frac{4}{3}$ B、 $\frac{4}{3}$ C、 $- \frac{3}{4}$ D、 $\frac{3}{4}$

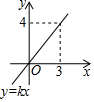查看试题解析
5. 下列计算正确的是（）

A、x⁵+x⁵＝x⁵ B、x³ $\cdot$ x³＝2x³ C、(﹣2x²)³＝8x⁸ D、x⁸÷x⁴＝x⁴

查看试题解析
6. 如图，在△ABC中，AB＝2，BC＝4，△ABC的高AD与CE的比为（）

A、1：2 B、2：1 C、1：4 D、4：1

查看试题解析
7. 已知一次函数y=kx﹣m﹣2x的图象与y轴的负半轴相交，且函数值y随自变量x的增大而减小，则下列结论正确的是（）

A、k＜2，m＞0 B、k＜2，m＜0 C、k＞2，m＞0 D、k＜0，m＜0

查看试题解析
8. 如图，⨀O是△ABC的外接圆，直径AD＝4，∠ABC＝∠DAC，则AC的长为（　　）

A、2 $\sqrt{2}$ B、2 C、4 D、6

查看试题解析
9. 若二次函数y＝(k+1)x²﹣2 $\sqrt{2}$ x+k的最高点在x轴上，则k的值为（）

A、1 B、2 C、﹣1 D、﹣2

查看试题解析

二、填空题

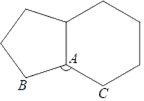
10. 在实数1，﹣ $\sqrt{5}$ ，0， $\sqrt{2}$ 中，最大的数.

查看试题解析
11. 如图，若正五边形和正六边形有一边重合，则∠BAC＝.

查看试题解析
12. 已知A(x₁ ， y₁)，B(x₂ ， y₂)都在反比例函数y＝ $\frac{6}{x}$ 的图象上.若x₁x₂＝﹣4，则y₁ $\cdot$ y₂的值为.

查看试题解析
13. 如图，四边形ABCD，四边形EBFG，四边形HMPN均是正方形，点E、F、P、N分别在边AB、BC、CD、AD上，点H、G、M在AC上，阴影部分的面积依次记为S₁ ， S₂ ，则S₁：S₂等于.

查看试题解析

三、解答题

14. 计算： $\sqrt{6}$ ×(﹣ $\sqrt{18}$ )+|2﹣3 $\sqrt{3}$ | $- {(- \frac{1}{2})}^{- 1}$

查看试题解析
15. 解方程： $\frac{x}{x - 2}$ ﹣ $\frac{1}{x^{2} - 4}$ ＝1

查看试题解析
16. 如图，已知△ABC，利用尺规在BC上找一点P，使得△ABP与△ACP均为直角三角形(不写作法，保留作图痕迹)

查看试题解析
17. 如图，E、F分别是矩形ABCD的对角线AC和BD上的点，且AE=DF。求证：BE=CF

查看试题解析

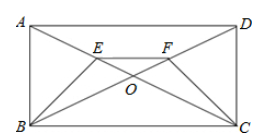18. 中国飞人苏炳添以6秒47获得2019年国际田联伯明翰室内赛男子60米冠军，苏炳添夺冠掀起跑步热潮某校为了解该校八年级男生的短跑水平，全校八年级男生中随机抽取了部分男生，对他们的短跑水平进行测试，并将测试成绩(满分10分)绘制成如下不完整的统计图表：

组别	成绩/分	人数/人
A	5	36
B	6	32
C	7	15
D	8	8
E	9	5
F	10	m

请你根据统计图表中的信息，解答下列问题：

(1)、填空：m＝， n＝；

(2)、所抽取的八年级男生短跑成绩的众数是分，扇形统计图中E组的扇形圆心角的度数为°；

(3)、求所抽取的八年级男生短跑的平均成绩.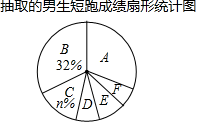

查看试题解析

19. 汉江是长江最长的支流，在历史上占居重要地位，陕西省境内的汉江为汉江上游段.李琳利用热气球探测器测量汉江某段河宽，如图，探测器在A处观测到正前方汉江两岸岸边的B、C两点，并测得B、C两点的俯角分别为45°，30°已知A处离地面的高度为80m，河平面BC与地面在同一水平面上，请你求出汉江该段河宽BC.(结果保留根号)

查看试题解析
20. 快递公司为提高快递分拣的速度，决定购买机器人来代替人工分拣，两种型号的机器人的工作效率和价格如表：

型号

甲

乙

每台每小时分拣快递件数(件)

1000

800

每台价格(万元)

5

3

该公司计划购买这两种型号的机器人共10台，并且使这10台机器人每小时分拣快递件数总和不少于8500件

(1)、设购买甲种型号的机器人x台，购买这10台机器人所花的费用为y万元，求y与x之间的关系式；

(2)、购买几台甲种型号的机器人，能使购买这10台机器人所花总费用最少？最少费用是多少？

查看试题解析
21. 西安市历史文化底蕴深厚，旅游资源丰富，钟楼、大雁塔兵马俑三个景点是人们节假日游玩的热门景点

(1)、李辉从这三个景点中随机选取一个景点去游玩，求他去钟楼的概率；

(2)、张慧、王丽两名同学，各自从三个景点中随机选取一个作为周末游玩的景点，用树状图或列表法求他们同时选中大雁塔的概率.

查看试题解析
22. 如图，AB是⨀O的直径，点C在⨀O上，AD和过C点的切线互相垂直，垂足为D

(1)、求证：AC平分∠DAB；

(2)、若点M是AB的中点，CM交AB于点N，求证：BM²＝MC•MN.

查看试题解析
23. 如图，已知抛物线C₁：y＝﹣x²+4，将抛物线C1沿x轴翻折，得到抛物线C₂

(1)、求出抛物线C₂的函数表达式；

(2)、现将抛物线C₁向左平移m个单位长度，平移后得到的新抛物线的顶点为M，与x轴的交点从左到右依次为A，B；将抛物线C₂向右也平移m个单位长度，平移后得到的新抛物线的顶点为N，与x轴交点从左到右依次为D，E.在平移过程中，是否存在以点A，N，E，M为顶点的四边形是矩形的情形？若存在，请求出此时m的值；若不存在，请说明理由.

查看试题解析
24. (1)如图1，A、B是⨀O上的两个点，点P在⨀O上，且△APB是直角三角形，⨀O的半径为1

(1)、①请在图1中画出点P的位置.
②当AB＝1时，∠APB＝°.

(2)、如图2，⨀O的半径为5，A、B为⨀O外固定两点(O、A、B三点不在同一直线上)，且OA＝9，P为⊙O上的一个动点(点P不在直线AB上)，以PA和AB为作平行四边形PABC，求BC的最小值，并确定此时点P的位置；

(3)、如图3，A、B是⊙O上的两个点，过A点作射线AM⊥AB，AM交⨀O于点C，若AB＝3，AC＝4，点D是平面内的一个动点，且CD＝2，E为BD的中点，在D的运动过程中，求线段AE长度的最大值与最小值.

查看试题解析

型号	甲	乙
每台每小时分拣快递件数(件)	1000	800
每台价格(万元)	5	3