广西壮族自治区贵港市港南区2019-2020学年七年级上学期数学期中考试试卷

试卷更新日期：2019-12-24 类型：期中考试

进入出卷网下载

一、单选题

1. 在﹣4，2，﹣1，3这四个数中，比﹣2小的数是（）

A、﹣4 B、2 C、﹣1 D、3

查看试题解析
2. 计算：|0﹣2019|＝（）

A、0 B、﹣2019 C、2019 D、±2019

查看试题解析
3. 如图，在数轴上表示互为相反数的两数的点是（）

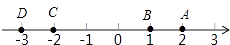A、点A和点C B、点B和点C C、点A和点B D、点B和点D

查看试题解析
4. 下列个组数中，数值相等的是（）.

A、 $3^{2}$ 和 $2^{3}$ B、 $- 2^{3}$ 和 ${(- 2)}^{3}$ C、 $- 3^{2}$ 和 ${(- 3)}^{2}$ D、 $- {(3 \times 2)}^{2}$ 和 $- 3 \times 2^{2}$

查看试题解析
5. 多项式 $4 x^{2} y - 5 x^{3} y^{2} + 7 {xy}^{3} - 6$ 的次数是 $($ 　　 $)$

A、4 B、5 C、3 D、2

查看试题解析
6. 下列各式中，去括号正确的是（）

A、a＋（b－c）=a－b－c B、a－（b＋c）=a－b＋c C、a＋2（b＋c）=a＋2b＋c D、a－2（b－c）=a－2b＋2c

查看试题解析
7. 若代数式4x－5与 $\frac{2 x - 1}{2}$ 的值相等，则x的值是（）

A、1 B、 $\frac{3}{2}$ C、 $\frac{2}{3}$ D、2

查看试题解析
8. 下列说法错误的是（）

A、多项式 $1 - x^{3} + x^{2}$ 是三次三项式 B、 $- x^{2} y^{3} z$ 是六次单项式 C、 $- 3 x^{2} y + 4 x - 1$ 的常数项是-1 D、单项式 $\frac{- x^{2} y}{2}$ 的系数为2

查看试题解析
9. 完全相同的4个小矩形如图所示放置，形成了一个长、宽分别为m，n的大长方形，则图中阴影部分的周长是

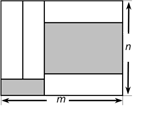A、4m B、4n C、2m＋n D、m＋2n

查看试题解析
10. 若 $x^{2} - x - 1 = 0$ ,则 $x^{3} - 2 x^{2} + 5$ 的值为（）

A、0 B、2 C、4 D、5

查看试题解析
11. 下列说法：①在数轴上表示 $- a$ 的点一定在原点的左边；②有理数 $a$ 的倒数是 $\frac{1}{a}$ ；③一个数的相反数一定小于或等于这个数；④如果 $a > b$ ，那么 $a^{2} > b^{2}$ ；⑤ $\frac{3 x^{2} y}{5}$ 的次数是2；⑥有理数可以分为整数、正分数、负分数和0；⑦ $- 7 m^{2} b a$ 与 $a b m^{2}$ 是同类项.其中正确的个数为（）

A、1个 B、2个 C、3个 D、4个

查看试题解析
12. 如果把向东走3km记作+3km ，那么-2km表示的实际意义是（　　）

A、向东走2km B、向西走2km C、向南走2km D、向北走2km

查看试题解析

二、填空题

13. 12的相反数是；的相反数是﹣2 $\frac{3}{4}$ ；﹣ $\frac{2}{3}$ 的绝对值是．

查看试题解析
14. 我国倡导的“一带一路”建设将促进我国与世界各国的互利合作，“一带一路”地区覆盖总人口约为4400000000人，将数据4400000000用科学记数法表示为.

查看试题解析
15. 小明写作业时，不慎将墨水滴在数轴上，根据图中数值，请你确定墨迹盖住部分的整数共有个.

查看试题解析
16. 数轴上的A点与表示﹣3的点距离4个单位长度，则A点表示的数为．

查看试题解析
17. 若 $| x - 2 | + | y + 3 | = 0$ ，则 $x - y =$ .

查看试题解析
18. 某些整数的所有正约数之和可以按如下方法求得，如：
$6 = 2 \times 3$ ，则6的所有正约数之和为 $(1 + 3) + (2 + 6) = (1 + 2) \times (1 + 3) = 12$ ；

$12 = 2^{2} \times 3$ ，则12的所有正约数之和为 $(1 + 3) + (2 + 6) + (4 + 12) = (1 + 2 + 2^{2}) \times (1 + 3)$ $= 28$

$36 = 2^{2} \times 3^{2}$ ，则36的所有正约数之和为 $(1 + 3 + 9) + (2 + 6 + 18) + (4 + 12 + 36)$ $= (1 + 2 + 2^{2}) \times (1 + 3 + 3^{2}) = 91$

参照上述方法，那么144的所有正约数之和为.

查看试题解析

三、解答题

19. 计算

(1)、 $- 2^{3} + {(3 - 7)}^{2} - 2 - {(- 1)}^{3}$

(2)、 $5 a - 7 b - 3 a + 2 b$

查看试题解析
20. 先化简再求值：（b+3a）﹣2（2﹣5b）﹣（1﹣2b﹣a），其中：a=2，b=1．

查看试题解析
21. 某电力检修小组，乘车沿一条南北走向的笔直公路检修线路，早晨从 $A$ 地出发晚上到达 $B$ 地，约定向南为正，向北为负，当天的行驶记录如下(单位：千米)5，-8，10，-7，18，-6，10，-5

(1)、 $B$ 地在 $A$ 地的南面，还是北面？与 $A$ 地相距多少千米？

(2)、若汽车每千米耗油 $a$ 升，这天汽车共耗油多少升？

查看试题解析
22. 已知：如图， $a = 10$ ， $b = 8$ ， $c = 12$ ，求阴影部分的面积(结果保留 $π$ ).

查看试题解析
23. 大客车上原有 $(3 a - b)$ 人，中途下车一半人，又上车若干人，这时车上共有乘客 $(8 a - 5 b)$ 人.

(1)、问：上车乘客有多少人？

(2)、在(1)的条件下，当 $a = 12$ ， $b = 10$ 时，上车乘客是多少人？

查看试题解析
24. 对于有理数，定义一种新运算“ $\oplus$ ”，观察下列各式：
$1 \oplus 2 = | 1 \times 4 - 2 | = 2$ ， $2 \oplus 8 = | 2 \times 4 - 8 | = 0$ ， $- 3 \oplus 4 = | - 3 \times 4 - 4 | = 16$ .

(1)、计算： $(- 4) \oplus 3 =$ ， $a \oplus b =$ .

(2)、若 $a \neq b$ ，则 $a \oplus b$ $b \oplus a$ (填入“ $=$ ”或“ $\neq$ ”).

(3)、若有理数 $a$ ， $b$ 在数轴上的对应点如图所示且 $\frac{1}{4} a \oplus (- b) = 5$ ，求 $[(a + b) \oplus (a + b)] \oplus (a + b)$ 的值.

查看试题解析
25. 观察下列三行数：
0，3，8，15，24，…①

2，5，10，17，26，…②

0，6，16，30，48，…③

(1)、第①行数按什么规律排的，请写出来？

(2)、第②、③行数与第①行数分别对比有什么关系？

(3)、取每行的第 $n$ 个数，求这三个数的和.

查看试题解析
26. 如图：在数轴上 $A$ 点表示数 $a$ ， $B$ 点表示数 $b$ ， $C$ 点表示数 $c$ ， $b$ 是最大的负整数，且 $a$ 、 $c$ 满足 $| a + 3 |$ 与 ${(c - 5)}^{2}$ 互为相反数.

(1)、 $a =$ ， $b =$ ， $c =$ .

(2)、若将数轴折叠，使得 $A$ 点与 $C$ 点重合，则点 $B$ 与数表示的点重合；

(3)、点 $A$ 、 $B$ 、 $C$ 开始在数轴上运动，若点 $A$ 以每秒2个单位长度的速度向左运动，同时，点 $B$ 和点 $C$ 分别以每秒1个单位长度和3个单位长度的速度向右运动，假设 $t$ 秒钟过后，若点 $A$ 与点 $B$ 之间的距离表示为 $A B$ ，点 $B$ 与点 $C$ 之间的距离表示为 $B C$ .
①请问： $3 B C - 2 A B$ 的值是否随着时间 $t$ 变化而改变？若变化，说明理由；若不变，请求其值.

②探究：在(3)的情况下，若点 $A$ 、 $C$ 向右运动，点 $B$ 向左运动，速度保持不变， $3 B C - 4 A B$ 值是否随着时间 $t$ 的变化而改变，若变化，请说明理由；若不变，请求其值.

查看试题解析