陕西省宝鸡市凤翔县2020届九年级上学期数学期中考试试卷

试卷更新日期：2019-12-24 类型：期中考试

进入出卷网下载

一、单选题

1. 下列各式中，是一元二次方程的是（）

A、 $3 x^{2} + \frac{1}{x} = 0$ B、 $2 x^{2} - 3 x + 1$ C、 $(x + 4) = 2 (x - 2)$ D、 $(3 x - 1) (3 x + 2) = 0$

查看试题解析
2. 用配方法解方程 $x^{2} - 2 x - 3 = 0$ 时，可变形为（）

A、 ${(x - 1)}^{2} = 2$ B、 ${(x - 1)}^{2} = 4$ C、 ${(x - 2)}^{2} = 2$ D、 ${(x - 2)}^{2} = 4$

查看试题解析
3. 关于x的一元二次方程3x²﹣4x+8＝0的根的情况是（　　）

A、有两个相等的实数根 B、有两个不相等的实数根 C、只有一个实数根 D、没有实数根

查看试题解析
4. 如图，在菱形ABCD中，E是AB的中点，F点是AC的中点，交AC于点F，如果EF＝4，那么菱形ABCD的周长为（　　）

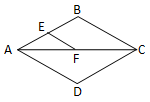A、9 B、12 C、32 D、24

查看试题解析
5. 已知平行四边形ABCD中，对角线AC、BD相交于O.则下列说法准确的是（）

A、当 $OA = OC$ 时，平行四边形ABCD为矩形 B、当 $AB = AD$ 时，平行四边形ABCD为正方形 C、当 $∠ ABC = 90^{°}$ 时，平行四边形ABCD为菱形 D、当 $AC ⊥ BD$ 时，平行四边形ABCD为菱形

查看试题解析
6. 在一个不透明的布袋中装有60个白球和若干个黑球，除颜色外其他都相同，小红每次摸出一个球并放回，通过多次试验后发现，摸到黑球的频率稳定在0.6左右，则布袋中黑球的个数可能有（）

A、24 B、36 C、40 D、90

查看试题解析
7. 已知直角三角形的两条直角边长恰好是方程x²－5x＋6＝0的两个根,则此直角三角形斜边长是（）

A、 $\sqrt{13}$ B、 $\sqrt{5}$ C、13 D、5

查看试题解析
8. 小华、小强和小彬三位同学随机地站成一排做游戏，小华站在排头的概率是（）

A、 $\frac{1}{2}$ B、 $\frac{1}{3}$ C、 $\frac{2}{3}$ D、1

查看试题解析
9. 在一幅长8分米，宽6分米的矩形风景画（如图甲）的四周镶宽度相同的金色纸边，制成一幅矩形挂图（如图乙），使整个挂图的面积是80平方分米，设金色纸边的宽度为x分米，则可列方程为（）

A、 $(8 + x) (6 + x) = 80$ B、 $(8 + 2 x) (6 + x) = 80$ C、 $(8 + 2 x) (6 + 2 x) = 80$ D、 $(8 + x) (6 + 2 x) = 80$

查看试题解析
10. 如图，正方形ABCD的边长为2，点E在对角线BD上，且 $∠ BAE = {22.5}^{°}$ ， $EF ⊥ AB$ ，垂足为F，则EF的长为（）

A、 $\sqrt{2} - 1$ B、 $2 - \sqrt{2}$ C、 $2 \sqrt{2} - 2$ D、 $4 - 2 \sqrt{2}$

查看试题解析

二、填空题

11. 一元二次方程3（x﹣5）²＝2（x﹣5）的解是.

查看试题解析
12. 一个菱形的边长为5，一条对角线长为6，则这个菱形另一条对角线长为.

查看试题解析
13. 甲、乙两人分别到A、B、C三个餐厅的其中一个用餐，那么甲乙在同一餐厅用餐的概率是.

查看试题解析
14. 关于x的一元二次方程 $(k - 2) x^{2} - 3 x + 2 = 0$ 有实数根，则k的取值范围为.

查看试题解析
15. 如图，如图，在正方形ABCD中，点P在AB边上， $A E ⊥ D P$ 于E点， $CF ⊥ DP$ 于F点，若 $A E = 4$ ， $C F = 7$ ，则 $E F =$ .

查看试题解析

三、解答题

16. 解下列方程

(1)、 $x^{2} - 4 x - 3 = 0$

(2)、 $3 x^{2} - 12 x = - 12$ （配方法）

查看试题解析
17. 如图，在菱形ABCD中，作 $BE ⊥ AD$ 于E，BF⊥CD于F，求证： $AE = CF$ .

查看试题解析
18. 甲、乙、丙、丁四名同学进行一次乒乓球单打比赛，要从中选两位同学打第一场比赛．

(1)、若由甲挑一名选手打第一场比赛，选中乙的概率是多少？（直接写出答案）

(2)、任选两名同学打第一场，请用树状图或列表法求恰好选中甲、乙两位同学的概率。

查看试题解析
19. 现代互联网技术的广泛应用.催生了快递行业的高度发展.据调查.长春市某家快递公司今年三月份完成投递的快递总件数为10万件，预计五月份完成投递的快递总件数将增加到12.1万件，现假定该公司每月投递的快递总件数的增长率相同，求该快递公司完成投递的快递总件数三月份到五月份的月平均增长率.

查看试题解析
20. 如图所示，O是矩形ABCD的对角线的交点，作 $DE ∥ AC$ ， $CE ∥ BD$ ，DE、CE相交于点E.求证：

(1)、四边形OCED是菱形；

(2)、连接OE.若 $AD = 4$ ， $CD = 3$ ，求OE的长.

查看试题解析
21. 国贸商店服装柜在销售中发现：“宝乐牌”童装平均每天可以售出20件，每件盈利40元.为了迎接“六一”儿童节，商场决定采取适当的降价措施，扩大销售量，增加盈利，尽快减少库存.经调查发现：每件童装每降价1元，商场平均每天可多销售2件.

(1)、若每件童装降价5元，则商场盈利多少元？

(2)、若商场每天要想盈利1200元，请你帮助商场算一算，每件童装应降价多少元？

查看试题解析
22. 操作与探究

(1)、操作：BD是矩形ABCD的对角线， $A B = 4$ ， $B C = 3$ ，将 $△ BAD$ 绕着点B顺时针旋转 $α$ （ $0^{°} < α < 360^{°}$ ）得到 $△ BEF$ ，点A、D的对应点分别为E、F.若点E落在BD上，如图①，求 $D E$ 的长.

(2)、探究：当点E落在线段DF上时，CD与BE交于点C.其它条件不变，如图②.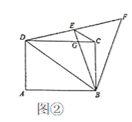

①求证： $△ ADB ≅ △ EDB$ ；

②求CG的长.

查看试题解析