广西壮族自治区玉林市博白县2020届九年级上学期数学期中考试试卷

试卷更新日期：2019-12-24 类型：期中考试

进入出卷网下载

一、单选题

1. 下列电视台的台标，是中心对称图形的是（）

A、 B、 C、 D、

查看试题解析
2. 一元二次方程 $x^{2} + 4 x = 2$ 配方后化为（）

A、 ${(x + 2)}^{2} = 6$ . B、 ${(x - 2)}^{2} = 6$ C、 ${(x + 2)}^{2} = - 6$ D、 ${(x + 2)}^{2} = - 2$

查看试题解析
3. 抛物线 $y = {(x + 2)}^{2} - 3$ 的顶点坐标是（）

A、（-2.-3） B、（2，3） C、（-2，3） D、（-3，2）

查看试题解析
4. 一元二次方程x²﹣2x+3＝0根的情况是（）

A、有两个不相等的实数根 B、有两个相等的实数根 C、没有实数根 D、无法判断

查看试题解析
5. 已知，抛物线 $y = a x^{2} + b x + c$ 与x轴的公共点是（-6，0），（2，0），则这条抛物线的对称轴是直线（）

A、 $x = 1$ B、 $x = - 2$ C、 $x = - 1$ D、 $x = 2$

查看试题解析
6. 抛物线 $y = 3 x^{2}$ 先向下平移1个单位，再向左平移2个单位，所得的抛物线是（）

A、 $y = 3 {(x + 2)}^{2} - 1$ . B、 $y = 3 {(x - 2)}^{2} + 1$ C、 $y = {(x - 2)}^{2} - 1$ D、 $y = 3 {(x + 2)}^{2} + 1$

查看试题解析
7. 关于x的一元二次方程 $(m - 2) x^{2} - 2 x - 1 = 0$ 有两个不相等的实数根，则实数m的取值范围是（）

A、 $m ⩾ 1$ 且 $m \neq 2$ B、 $m > 1$ C、 $m > 1$ 且 $m \neq 2$ D、 $m \neq 2$

查看试题解析
8. 在同一坐标系中，一次函数y=ax+2与二次函数y=x²﹣a的图象可能是（）

A、 B、 C、 D、

查看试题解析
9. 如图，等腰直角三角形ABC的直角边AB的长为 $\sqrt{3}$ ，将△ABC绕点A逆时针旋转15°后得到△AB′C′，AC与B′C′相交于点D，则图中阴影△ADC′的面积等于（）

A、 $\frac{3 \sqrt{3}}{2} {cm}^{2}$ B、 $\frac{3 - \sqrt{3}}{2} c m^{2}$ C、 $2 \sqrt{3} {cm}^{2}$ D、 $6 {cm}^{2}$

查看试题解析
10.
如图，小明家的住房平面图呈长方形，被分割成3个正方形和2个长方形后仍是中心对称图形．若只知道原住房平面图长方形的周长，则分割后不用测量就能知道周长的图形的标号为（）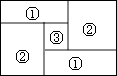

A、①② B、②③ C、①③ D、①②③

查看试题解析
11. 某旅游景点8月份共接待游客25万人次，10月份共接待游客64万人次，设每个月的平均增长率为x，可列方程为（）

A、 $25 {(1 + x)}^{2} = 64$ B、 $64 {(1 + x)}^{2} = 25$ C、 $25 {(1 - x)}^{2} = 64$ D、 $64 {(1 - x)}^{2} = 25$

查看试题解析
12. 二次函数 $y = a x^{2} + b x + c$ （ $a \neq 0$ ）的图象如图所示，对称轴为 $x = 1$ ，给出下列结论：① $a b c > 0$ ； ②当 $x > 2$ 时， $y > 0$ ；③ $3 a + c > 0$ ；④ $3 a + b > 0$ ，其中正确的结论有（）

A、①② B、①③ C、①③④ D、②④

查看试题解析

二、填空题

13. 点M（2，-4）关于原点对称的点的坐标是.

查看试题解析
14. 方程 $x^{2} = x$ 的根是．

查看试题解析
15. 关于 $x$ 的一元二次方程 $(m - 1) x^{2} + x + m^{2} + 2 = 0$ 有一根为2，则 $m$ 的值为.

查看试题解析
16. 如图， $△ O D C$ 是由 $△ O A B$ 绕点O顺时针旋转40°后得到的图形，若点D恰好落在AB上，且 $∠ A O C = 100^{°}$ ，则 $∠ B$ 的度数是°.

查看试题解析
17. 已知关于x的方程2+（x﹣m）（x﹣n）＝0，存在a，b是方程2+（x﹣m）（x﹣n）＝0的两个根，则实数m，n，a，b的大小关系可能是.

查看试题解析
18. 如图所示，四边形ABCD是边长为3的正方形，点E在BC上，BE＝1，△ABE绕点A逆时针旋转后得到△ADF，则FE的长等于.

查看试题解析

三、解答题

19. 解下列方程：

(1)、 $x^{2} - x = 6$

(2)、 $4 x^{2} - 8 = 3 x (1 + x)$

查看试题解析
20. 如图所示，△ABC直角三角形，延长AB到D，使BD=BC，在BC上取BE=AB，连接DE.△ABC顺时针旋转后能与△EBD重合，那么：

(1)、旋转中心是哪一点？旋转角是多少度？

(2)、AC与DE的关系怎样？请说明理由.

查看试题解析
21. 二次函数 $y = a x^{2} - 2 x + 5$ 与直线 $y = - 2 x + 3$ 交于点 $P (- 1, b)$ .

(1)、求出此二次函数的解析式；

(2)、求此二次函数的顶点坐标，并指出x取何值时，该函数的y随x的增大而减小。

查看试题解析
22. 已知 $x_{1}, x_{2}$ 是一元二次方程 $2 x^{2} - 2 x + m + 1 = 0$ 的两个实数根.

(1)、求实数m的取值范围；

(2)、如果 $x_{1}, x_{2}$ 满足不等式 $4 + 4 x_{1} x_{2} > x_{1}^{2} + x_{2}^{2}$ ，且m为整数，求m的值。

查看试题解析
23. △ABC 在平面直角坐标系中的位置如图所示，其中每个小正方形的边长为 1 个单位长度.

①画出△ABC 关于原点 O 的中心对称图形△A1B1C1，并写出点 A1的坐标；

②将△ABC 绕点 C 顺时针旋转 90°得到△A2B2C，画出△A2B2C，求在旋转过程中，点 A所经过的路径长

查看试题解析
24. 元旦期间，某宾馆有50个房间供游客居住，当每个房间每天的定价为180元时，房间会全部住满；当每个房间每天的定价每增加10元时，就会有一个房间空闲.如果游客居住房间，宾馆需对每个房间每天支出20元的各种费用.

(1)、若房价定为200元时，求宾馆每天的利润；

(2)、房价定为多少时，宾馆每天的利润最大？最大利润是多少？

查看试题解析
25. 如图，在▱ABCD中，AB=1，BC= $\sqrt{5}$ ，对角线AC，BD交于O点，将直线AC绕点O顺时针旋转，分别交于BC，AD于点E，F.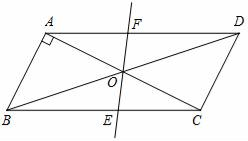

(1)、证明：当旋转角为时，四边形ABEF是平行四边形；

(2)、在旋转过程中，四边形BEDF可能是菱形吗？如果不可能，请说明理由；如果可能，说明理由并求出此时AC绕点O顺时针旋转的度数.

查看试题解析
26. 如图，已知直线y=-x+3与x轴、y轴分别交于A，B两点，抛物线y=-x²+bx+c经过B点，且与x轴交于C，D两点（点C在左侧），且C(-3，0).

(1)、求抛物线的解析式；

(2)、平移直线AB，使得平移后的直线与抛物线分别交于点D，E，与y轴交于点F，连接CE，CF，求△CEF的面积.

查看试题解析