广西壮族自治区河池市凤山县2020届九年级上学期数学期中考试试卷
试卷更新日期:2019-12-24 类型:期中考试
一、单选题
-
1. 下列手机手势解锁图案中,是中心对称图形的是( )A、
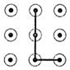 B、
B、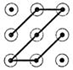 C、
C、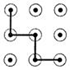 D、
D、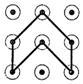 2. 下列方程中,关于x的一元二次方程是( )A、 B、 C、 D、3. 点P(2,﹣1)关于原点对称的点P′的坐标是( )A、(﹣2,1) B、(﹣2,﹣1) C、(﹣1,2) D、(1,﹣2)4. 用配方法解方程 ,配方正确的是( )A、 B、 C、 D、5. 抛物线y=(x+2)2﹣3可以由抛物线y=x2平移得到,则下列平移过程正确的是( )A、先向左平移2个单位,再向上平移3个单位 B、先向左平移2个单位,再向下平移3个单位 C、先向右平移2个单位,再向下平移3个单位 D、先向右平移2个单位,再向上平移3个单位6. 若 ,则 的值为( )A、7 B、-3 C、7或-3 D、217. 关于x的一元二次方程 有两个不相等的实数根,则实数m的取值范围为( )A、 B、 C、 D、8. 下图是几种汽车轮毂的图案,图案绕中心旋转90°后能与原来的图案重合的是( )A、
2. 下列方程中,关于x的一元二次方程是( )A、 B、 C、 D、3. 点P(2,﹣1)关于原点对称的点P′的坐标是( )A、(﹣2,1) B、(﹣2,﹣1) C、(﹣1,2) D、(1,﹣2)4. 用配方法解方程 ,配方正确的是( )A、 B、 C、 D、5. 抛物线y=(x+2)2﹣3可以由抛物线y=x2平移得到,则下列平移过程正确的是( )A、先向左平移2个单位,再向上平移3个单位 B、先向左平移2个单位,再向下平移3个单位 C、先向右平移2个单位,再向下平移3个单位 D、先向右平移2个单位,再向上平移3个单位6. 若 ,则 的值为( )A、7 B、-3 C、7或-3 D、217. 关于x的一元二次方程 有两个不相等的实数根,则实数m的取值范围为( )A、 B、 C、 D、8. 下图是几种汽车轮毂的图案,图案绕中心旋转90°后能与原来的图案重合的是( )A、 B、
B、 C、
C、 D、
D、 9. 如图,在△ABC中,AB=8,AC=6,∠BAC=30°,将△ABC绕点A逆时针旋转60°得到△AB1C1 , 连接BC1 , 则BC1的长为( )
9. 如图,在△ABC中,AB=8,AC=6,∠BAC=30°,将△ABC绕点A逆时针旋转60°得到△AB1C1 , 连接BC1 , 则BC1的长为( )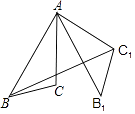 A、6 B、8 C、10 D、1210. 二次函数y=ax2+bx+c的自变量x与函数y的对应值如下表:
A、6 B、8 C、10 D、1210. 二次函数y=ax2+bx+c的自变量x与函数y的对应值如下表:x
…
-5
-4
-3
-2
-1
0
…
y
…
4
0
-2
-2
0
4
…
下列说法正确的是( )
A、抛物线的开口向下 B、当x>-3时,y随x的增大而增大 C、二次函数的最小值是-2 D、抛物线的对称轴是直线x=-11. 我县九州村某梨园2016年产量为1000吨,2018年产量为1440吨,求该梨园梨产量的年平均增长率,设该梨园梨产量的年平均增长量为x , 则根据题意可列方程为A、1440(1-x)2= 1000 B、1440(1+x)2= 1000 C、1000(1-x)2= 1440 D、1000(1+x)2= 144012. 设一元二次方程 的两根分别为 ,且 ,则满足( )
A、 B、 C、 D、 且二、填空题
-
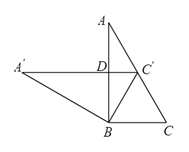
13. 一元二次方程 的二次项系数是.14. 抛物线 的顶点坐标是.15. 已知m是关于x的方程 的一个根,则 = .16. 如图,两块相同的三角板完全重合在一起,∠A=30°,AC=10,把上面一块绕直角顶点B逆时针旋转到△A′BC′的位置,点C′在AC上,A′C′与AB相交于点D,则BC′=.
 17. 已知二次函数 ,在 内,函数的最小值为.18. 二次函数y=ax2+bx+c(a≠0)图象如图,下列结论:①abc>0;②2a+b=0;③a-b+c>0;④当x≠1时,a+b>ax2+bx:⑤4ac<b2.其中正确的有(只填序号).
17. 已知二次函数 ,在 内,函数的最小值为.18. 二次函数y=ax2+bx+c(a≠0)图象如图,下列结论:①abc>0;②2a+b=0;③a-b+c>0;④当x≠1时,a+b>ax2+bx:⑤4ac<b2.其中正确的有(只填序号).
三、解答题
-
19. 解方程(1)、 ;(2)、 .20. 已知△ABC的三个顶点的坐标分别为 , , .
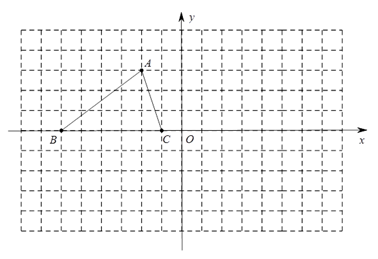 (1)、点A关于y轴对称的点的坐标是;(2)、将△ABC绕坐标原点O顺时针旋转180°,画出图形,直接写出点B的对应点的坐标;(3)、请直接写出:以A,B,C为顶点的平行四边形的第四个顶点D的坐标.21. 如图,点E是正方形ABCD的边AB上一点,AB=4,DE=4.3,△DAE逆时针旋转后能够与△DCF重合.
(1)、点A关于y轴对称的点的坐标是;(2)、将△ABC绕坐标原点O顺时针旋转180°,画出图形,直接写出点B的对应点的坐标;(3)、请直接写出:以A,B,C为顶点的平行四边形的第四个顶点D的坐标.21. 如图,点E是正方形ABCD的边AB上一点,AB=4,DE=4.3,△DAE逆时针旋转后能够与△DCF重合. (1)、旋转中心是 , 旋转角为∘;(2)、请你判断△DFE的形状,简单说明理由;(3)、四边形DEBF的面积为.22. 二次函数y=ax2+bx+c(a≠0)的图象如图所示,根据图象回答下列问题:
(1)、旋转中心是 , 旋转角为∘;(2)、请你判断△DFE的形状,简单说明理由;(3)、四边形DEBF的面积为.22. 二次函数y=ax2+bx+c(a≠0)的图象如图所示,根据图象回答下列问题: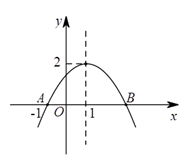 (1)、点B的坐标为;(2)、y随x的增大而减小的自变量x的取值范围为;(3)、方程ax2+bx+c=0的两个根为;(4)、不等式ax2+bx+c<0的解集为.23. 某种流感病毒,有一人患了这种流感,在每轮传染中一人将平均传给x人:(1)、第一轮后患病的人数为;(用含x的代数式表示)(2)、在进入第二轮传染之前,有两位患者被及时隔离并治愈,问第二轮传染后总共是否会有21人患病的情况发生,请说明理由.24. 某商场购进一种每件价格为100元的新商品,在商场试销发现:销售单价x(元/件)与每天销售量y(件)之间满足如图所示的关系:
(1)、点B的坐标为;(2)、y随x的增大而减小的自变量x的取值范围为;(3)、方程ax2+bx+c=0的两个根为;(4)、不等式ax2+bx+c<0的解集为.23. 某种流感病毒,有一人患了这种流感,在每轮传染中一人将平均传给x人:(1)、第一轮后患病的人数为;(用含x的代数式表示)(2)、在进入第二轮传染之前,有两位患者被及时隔离并治愈,问第二轮传染后总共是否会有21人患病的情况发生,请说明理由.24. 某商场购进一种每件价格为100元的新商品,在商场试销发现:销售单价x(元/件)与每天销售量y(件)之间满足如图所示的关系: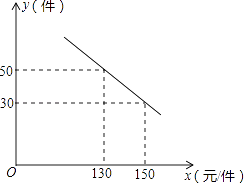 (1)、求出y与x之间的函数关系式;(2)、写出每天的利润W与销售单价x之间的函数关系式;若你是商场负责人,会将售价定为多少,来保证每天获得的利润最大,最大利润是多少?25. 如图,在等边△ABC中,点D为△ABC内的一点,∠ADB=120°,∠ADC=90°,将△ABD绕点A逆时针旋转60°得△ACE,连接DE.
(1)、求出y与x之间的函数关系式;(2)、写出每天的利润W与销售单价x之间的函数关系式;若你是商场负责人,会将售价定为多少,来保证每天获得的利润最大,最大利润是多少?25. 如图,在等边△ABC中,点D为△ABC内的一点,∠ADB=120°,∠ADC=90°,将△ABD绕点A逆时针旋转60°得△ACE,连接DE. (1)、求证:AD=DE;(2)、求∠DCE的度数;(3)、若BD=1,求AD,CD的长.26. 如图,已知二次函数y=ax2+bx+c的图象与x轴相交于A(﹣1,0),B(3,0)两点,与y轴相交于点C(0,﹣3).
(1)、求证:AD=DE;(2)、求∠DCE的度数;(3)、若BD=1,求AD,CD的长.26. 如图,已知二次函数y=ax2+bx+c的图象与x轴相交于A(﹣1,0),B(3,0)两点,与y轴相交于点C(0,﹣3).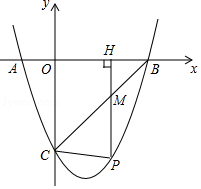 (1)、求这个二次函数的表达式;(2)、若P是第四象限内这个二次函数的图象上任意一点,PH⊥x轴于点H,与BC交于点M,连接PC.
(1)、求这个二次函数的表达式;(2)、若P是第四象限内这个二次函数的图象上任意一点,PH⊥x轴于点H,与BC交于点M,连接PC.①求线段PM的最大值;
②当△PCM是以PM为一腰的等腰三角形时,求点P的坐标.