广西壮族自治区桂林市灌阳县2020届九年级上学期数学期中考试试卷
试卷更新日期:2019-12-24 类型:期中考试
一、单选题
-
1. 函数 的图象经过( )A、(2,1) B、(1,1) C、(-1,2) D、(2,2)2. 下列方程是一元二次方程的是( )A、 B、 C、 D、3. 若关于 的一元二次方程 的一个根是 ,则 的值是( )A、2011 B、2015 C、2019 D、20204. 已知反比例函数 的图象位于第二、四象限,则 的取值范围为( )A、 B、 C、 D、5. 反比例函数 的图象上有两点 , ,若 ,则下列结论正确的是( )A、 B、 C、 D、6. 在反比例函数y= 的每一条曲线上,y都随着x的增大而减小,则k的值可以是( )A、-1 B、1 C、2 D、37. 下列各组的四条线段是成比例线段的是( )A、 B、 C、 D、8. 如图.利用标杆BE测量建筑物的高度.已知标杆BE高1.2m , 测得AB=1.6m . BC=12.4m . 则建筑物CD的高是( )
 A、9.3m B、10.5m C、12.4m D、14m9. 下列每组的两个图形中,不是位似图形的是( )A、
A、9.3m B、10.5m C、12.4m D、14m9. 下列每组的两个图形中,不是位似图形的是( )A、 B、
B、 C、
C、 D、
D、 10. 从正方形铁片上截去2cm宽的一个长方形,剩余矩形的面积为80cm2 , 则原来正方形的面积为( )A、100cm2 B、121cm2 C、144cm2 D、169cm211. 在平面直角坐标系中,直线y=x+b与双曲线 只有一个公共点,则b的值是( )A、1 B、±1 C、±2 D、212. 如图,点B是反比例函数 图象上的一点,矩形OABC的周长是20,正方形OCDF与正方形BCGH的面积之和为68,则 的值为( )
10. 从正方形铁片上截去2cm宽的一个长方形,剩余矩形的面积为80cm2 , 则原来正方形的面积为( )A、100cm2 B、121cm2 C、144cm2 D、169cm211. 在平面直角坐标系中,直线y=x+b与双曲线 只有一个公共点,则b的值是( )A、1 B、±1 C、±2 D、212. 如图,点B是反比例函数 图象上的一点,矩形OABC的周长是20,正方形OCDF与正方形BCGH的面积之和为68,则 的值为( )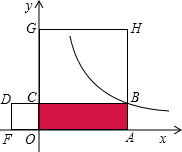 A、8 B、-8 C、16 D、-16
A、8 B、-8 C、16 D、-16二、填空题
-
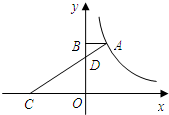
13. 若|x2﹣4x+4|与 互为相反数,则x+y的值为.14. 反比例函数 的比例系数是.15. 若 的一元二次方程 有两个不相等的实数根,则 的取值范围是.16. 如果关于 的一元二次方程 的一个根为1,则另一为.17. 如果关于 的一元二次方程 的两实数根互为倒数,则 的值为18. 如图,A是反比例函数 图象上的一点,点B、D在 轴正半轴上, 是 关于点D的位似图形,且 与 的位似比是1:3, 的面积为1,则 的值为.
三、解答题
-
19. 选择合适的方法解下列方程:(1)、(2)、20. 当 为何值时,代数式 的值与 的值互为相反数?21. 在一个可以改变体积的密闭容器内装有一定质量的二氧化碳,当改变容器的体积时,气体的密度也会随之改变,密度 (单位: )是体积 (单位: )的反比例函数,它的图象如图所示:
 (1)、求 与 之间的函数关系式,并写出自变量 的取值范围;(2)、求当 时气体的密度 .22. 已知 三个顶点的坐标分别 .
(1)、求 与 之间的函数关系式,并写出自变量 的取值范围;(2)、求当 时气体的密度 .22. 已知 三个顶点的坐标分别 . (1)、画出 ;(2)、以B为位似中心,将 放大到原来的2倍,在右图的网格图中画出放大后的图形△ ;(3)、写出点A的对应点 的坐标23. 求证:相似三角形对应中线的比等于相似比。(结合图形写出已知、求证并证明)24. 在国庆阅兵仪式上,三军女兵方队共378人,其中领队3人,方队中每排的人数比排数多10人,请你计算一下,三军女兵方队共有多少排?每排多少人?25. 如图,在平面直角坐标系中, 的直角顶点A在 轴上,OB=5,OA=4,动点M从点A出发,以每秒1个单位长度的速度,沿AO向终点O运动,同时点N从点O出发,以每秒2个单位长度的速度,沿OB向终点B移动,当两个动点运动了 秒时,解答下列问题:
(1)、画出 ;(2)、以B为位似中心,将 放大到原来的2倍,在右图的网格图中画出放大后的图形△ ;(3)、写出点A的对应点 的坐标23. 求证:相似三角形对应中线的比等于相似比。(结合图形写出已知、求证并证明)24. 在国庆阅兵仪式上,三军女兵方队共378人,其中领队3人,方队中每排的人数比排数多10人,请你计算一下,三军女兵方队共有多少排?每排多少人?25. 如图,在平面直角坐标系中, 的直角顶点A在 轴上,OB=5,OA=4,动点M从点A出发,以每秒1个单位长度的速度,沿AO向终点O运动,同时点N从点O出发,以每秒2个单位长度的速度,沿OB向终点B移动,当两个动点运动了 秒时,解答下列问题: (1)、若点B在反比例函数 的图象上,求出该函数的解析式;(2)、在两个动点运动过程中,当 为何值时,使得以O,M,N为顶点的三角形与 相似?26. 如图,已知点A(1,a)是反比例函数y1= 的图象上一点,直线y2=﹣ 与反比例函数y1= 的图象的交点为点B、D,且B(3,﹣1),求:
(1)、若点B在反比例函数 的图象上,求出该函数的解析式;(2)、在两个动点运动过程中,当 为何值时,使得以O,M,N为顶点的三角形与 相似?26. 如图,已知点A(1,a)是反比例函数y1= 的图象上一点,直线y2=﹣ 与反比例函数y1= 的图象的交点为点B、D,且B(3,﹣1),求: (1)、求反比例函数的解析式;(2)、求点D坐标,并直接写出y1>y2时x的取值范围;(3)、动点P(x,0)在x轴的正半轴上运动,当线段PA与线段PB之差达到最大时,求点P的坐标.
(1)、求反比例函数的解析式;(2)、求点D坐标,并直接写出y1>y2时x的取值范围;(3)、动点P(x,0)在x轴的正半轴上运动,当线段PA与线段PB之差达到最大时,求点P的坐标.