广西壮族自治区贵港市港南区2020届九年级上学期数学期中考试试卷
试卷更新日期:2019-12-24 类型:期中考试
一、单选题
-
1. 的值是( )A、 B、 C、 D、2. 要反映台州市某一周每天的最高气温的变化趋势,宜采用( )A、条形统计图 B、扇形统计图 C、折线统计图 D、频数分布统计图3. 若△ABC∽△DEF,且S△ABC:S△DEF=3:4,则其相似比为( )A、3:4 B、4:3 C、 :2 D、2:4. 已知关于 的方程 的一个根为-1,则实数 的值为( )A、1 B、-1 C、3 D、-35. 方程 的根为( )A、 B、 C、 , D、 ,6. 三角形两边的长是3和4,第三边的长是方程x2-12x+35=0的根,则该三角形的周长为( )A、14 B、12 C、12或14 D、以上都不对7. 反比例函数y= (k≠0)的图象经过点(2,-4),若点(4,n)在反比例函数的图象上,则n等于( )A、﹣8 B、﹣4 C、﹣ D、﹣28. 若点A(3,4)是反比例函数 图象上一点,则下列说法正确的是( )A、图象分别位于二、四象限 B、点(2,﹣6)在函数图象上 C、当x<0时,y随x的增大而减小 D、当y≤4时,x≥39. 我校图书馆三月份借出图书70本,计划四、五月份共借出图书220本,设四、五月份借出的图书每月平均增长率为x,则根据题意列出的方程是( )A、70(1+x)2=220 B、70(1+x)+70(1+x)2=220 C、70(1﹣x)2=220 D、70+70(1+x)+70(1+x)2=22010. 如图,在平直角坐标系中,过 轴正半轴上任意一点 作 轴的平行线,分别交函数 、 的图象于点 、点 .若 是 轴上任意一点,则 的面积为( )
 A、9 B、6 C、 D、311. 如图, , , , , , , ,则 的度数为( )
A、9 B、6 C、 D、311. 如图, , , , , , , ,则 的度数为( )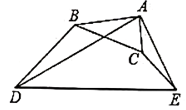 A、 B、 C、 D、无法确定12. 如图,在正方形 中, 是等边三角形, 、 的延长线分别交 于点 、 ,连接 、 , 与 相交于点 ,给出下列结论:① ;② ;③ ;④ .其中正确的个数是( )
A、 B、 C、 D、无法确定12. 如图,在正方形 中, 是等边三角形, 、 的延长线分别交 于点 、 ,连接 、 , 与 相交于点 ,给出下列结论:① ;② ;③ ;④ .其中正确的个数是( )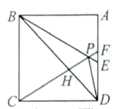 A、1 B、2 C、3 D、4
A、1 B、2 C、3 D、4二、填空题
-
13. 若反比例函数 的图象有一支在第二象限,则 的取值范围是.14. 若 , 是一元二次方程 的两个根,则 .15. 若 ,则 =.16. 如图,在 中,点 在线段 上, , , ,那么 .
 17. 如图,点 , 分别在 的边 , 的延长线上, .若 , 的面积为3,则 的面积为.
17. 如图,点 , 分别在 的边 , 的延长线上, .若 , 的面积为3,则 的面积为. 18. 如图,有一块三角形余料 , ,高线 ,要把它加工成一个矩形零件,使矩形的一边在 上,点 , 分别在 , 上,若满足 ,则 的长为.
18. 如图,有一块三角形余料 , ,高线 ,要把它加工成一个矩形零件,使矩形的一边在 上,点 , 分别在 , 上,若满足 ,则 的长为.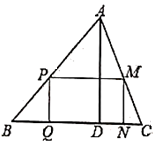
三、解答题
-
19.(1)、计算: .(2)、解方程: .20. 如图, ,在线段 上求作一点 ,使 .(不写作法,保留作图痕迹)
 21. 如图所示,双曲线 与直线 ( 为常数)交于 , 两点.
21. 如图所示,双曲线 与直线 ( 为常数)交于 , 两点. (1)、求双曲线 的表达式;(2)、根据图象观察,当 时,求 的取值范围;(3)、求 的面积.22. 学校为了解全校 名学生双休日在家最爱选择的电视频道情况,问卷要求每名学生从“新闻,体育,电影,科教,其他”五项中选择其一,随机抽取了部分学生,调查结果绘制成未完成的统计图表如下:
(1)、求双曲线 的表达式;(2)、根据图象观察,当 时,求 的取值范围;(3)、求 的面积.22. 学校为了解全校 名学生双休日在家最爱选择的电视频道情况,问卷要求每名学生从“新闻,体育,电影,科教,其他”五项中选择其一,随机抽取了部分学生,调查结果绘制成未完成的统计图表如下:频道
新闻
体育
电影
科教
其他
人数
(1)、求调查的学生人数及统计图表中 的值;(2)、求选择其他频道在统计图中对应扇形的圆心角的度数;(3)、求全校最爱选择电影频道的学生人数. 23. 小琴的父母承包了一块荒山地种植一批梨树,今年收获一批金溪密梨,小琴的父母打算以m元/斤的零售价销售5000斤密梨;剩余的5000(m+1)斤密犁以比零售价低1元的批发价批给外地客商,预计总共可赚得55 000元的毛利润.
23. 小琴的父母承包了一块荒山地种植一批梨树,今年收获一批金溪密梨,小琴的父母打算以m元/斤的零售价销售5000斤密梨;剩余的5000(m+1)斤密犁以比零售价低1元的批发价批给外地客商,预计总共可赚得55 000元的毛利润. (1)、求小琴的父母今年共收获金溪密梨多少斤?(2)、若零售金溪密梨平均每天可售出200斤,每斤盈利2元.为了加快销售和获得较好的售价,采取了降价措施,发现销售单价每降低0.1元,平均每天可多售出40斤,应降价多少元?每天销售利润为600元.24. 如图,某市郊外景区内一条笔直的公路 经过 、 两个景点,景区管委会又开发了风景优美的景点 .经测量, 位于 的北偏东 的方向上, 的北偏东 的方向上,且 .
(1)、求小琴的父母今年共收获金溪密梨多少斤?(2)、若零售金溪密梨平均每天可售出200斤,每斤盈利2元.为了加快销售和获得较好的售价,采取了降价措施,发现销售单价每降低0.1元,平均每天可多售出40斤,应降价多少元?每天销售利润为600元.24. 如图,某市郊外景区内一条笔直的公路 经过 、 两个景点,景区管委会又开发了风景优美的景点 .经测量, 位于 的北偏东 的方向上, 的北偏东 的方向上,且 . (1)、求景点 与 的距离.(2)、求景点 与 的距离.(结果保留根号)25. 何老师安排喜欢探究问题的小明解决某个问题前,先让小明看了一个有解答过程的例题.
(1)、求景点 与 的距离.(2)、求景点 与 的距离.(结果保留根号)25. 何老师安排喜欢探究问题的小明解决某个问题前,先让小明看了一个有解答过程的例题.例:若 ,求m和n的值.
解:因为
所以
所以
所以 所以
为什么要对 进行了拆项呢?
聪明的小明理解了例题解决问题的方法,很快解决了下面两个问题.相信你也能很好的解决下面的这两个问题,请写出你的解题过程.
解决问题:
(1)、若 ,求 的值;(2)、已知 满足 ,求 的值.26.(1)、如图1所示,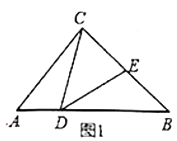
在 中, , ,点 在斜边 上,点 在直角边 上,若 ,求证: .
(2)、如图2所示,

在矩形 中, , ,点 在 上,连接 ,过点 作 交 (或 的延长线)于点 .
①若 ,求 的长;
②若点 恰好与点 重合,请在备用图上画出图形,并求 的长.