广西壮族自治区玉林市博白县2019-2020学年八年级上学期数学期中考试试卷
试卷更新日期:2019-12-24 类型:期中考试
一、单选题
-
1. 下面四个交通标志图中为轴对称图形的是( )
A、 B、
B、 C、
C、 D、
D、 2. 三角形两边长为2,5,则第三边的长不能是( )A、3 B、4 C、5 D、63. 下列四个图形中,线段BE是△ABC的高的是( )A、
2. 三角形两边长为2,5,则第三边的长不能是( )A、3 B、4 C、5 D、63. 下列四个图形中,线段BE是△ABC的高的是( )A、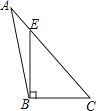 B、
B、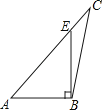 C、
C、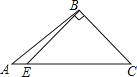 D、
D、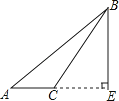 4. 等腰三角形的一个底角是 ,则它的顶角是( )A、 B、 C、 D、5. 下列图形不具有稳定性的是( )A、
4. 等腰三角形的一个底角是 ,则它的顶角是( )A、 B、 C、 D、5. 下列图形不具有稳定性的是( )A、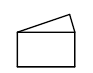 B、
B、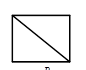 C、
C、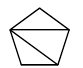 D、
D、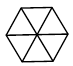 6. 在△ABC中,∠A,∠B都是锐角,则∠C是( )A、锐角 B、直角 C、钝角 D、以上都有可能7. 如图,下列说法中错误的是( )
6. 在△ABC中,∠A,∠B都是锐角,则∠C是( )A、锐角 B、直角 C、钝角 D、以上都有可能7. 如图,下列说法中错误的是( ) A、 不是三角形 的外角 B、 C、 是三角形 的外角 D、8. 不能确定两个三角形全等的条件是( )A、三边对应相等 B、两边及其夹角相等 C、两角和任一边对应相等 D、三个角对应相等9. 用直尺和圆规作一个角的平分线如图所示,说明∠AOC=∠BOC的依据是( ).
A、 不是三角形 的外角 B、 C、 是三角形 的外角 D、8. 不能确定两个三角形全等的条件是( )A、三边对应相等 B、两边及其夹角相等 C、两角和任一边对应相等 D、三个角对应相等9. 用直尺和圆规作一个角的平分线如图所示,说明∠AOC=∠BOC的依据是( ). A、SSS B、ASA C、AAS D、角平分线上的点到角两边距离相等10. 如图,五边形ABCDE中有一正三角形ACD,若AB=DE,BC=AE,∠E=115°,则∠BAE的度数为何?( )
A、SSS B、ASA C、AAS D、角平分线上的点到角两边距离相等10. 如图,五边形ABCDE中有一正三角形ACD,若AB=DE,BC=AE,∠E=115°,则∠BAE的度数为何?( )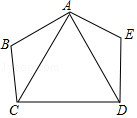 A、115 B、120 C、125 D、13011. 如图,在△ABC中,∠ACB=90°,分别以点A和点C为圆心,以相同的长(大于 AC)为半径作弧,两弧相交于点M和点N,作直线MN交AB于点D,交AC于点E,连接CD.下列结论错误的是( )
A、115 B、120 C、125 D、13011. 如图,在△ABC中,∠ACB=90°,分别以点A和点C为圆心,以相同的长(大于 AC)为半径作弧,两弧相交于点M和点N,作直线MN交AB于点D,交AC于点E,连接CD.下列结论错误的是( ) A、AD=CD B、∠A=∠DCE C、∠ADE=∠DCB D、∠A=2∠DCB12. 如图,点B、C、E在同一条直线上,△ABC与△CDE都是等边三角形,则下列结论不一定成立的是( )
A、AD=CD B、∠A=∠DCE C、∠ADE=∠DCB D、∠A=2∠DCB12. 如图,点B、C、E在同一条直线上,△ABC与△CDE都是等边三角形,则下列结论不一定成立的是( )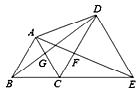 A、△ACE≌△BCD B、△BGC≌△AFC C、△DCG≌△ECF D、△ADB≌△CEA
A、△ACE≌△BCD B、△BGC≌△AFC C、△DCG≌△ECF D、△ADB≌△CEA二、填空题
-
13. 如图,在 中, ,则 的度数是.
 14. 在平面直角坐标系中,点 关于x轴对称的点的坐标是.15. 一个多边形的每一个外角都等于36°,则该多边形的内角和等于 度.16. 如图,在△ABC中,已知∠ABC=66°,∠ACB=54°,BE是AC上的高,CF是AB上的高,H是BE和CF的交点,∠EHF的度数是.
14. 在平面直角坐标系中,点 关于x轴对称的点的坐标是.15. 一个多边形的每一个外角都等于36°,则该多边形的内角和等于 度.16. 如图,在△ABC中,已知∠ABC=66°,∠ACB=54°,BE是AC上的高,CF是AB上的高,H是BE和CF的交点,∠EHF的度数是. 17. 如图,在 中, , ,AD是 的中线,AE是 的角平分线, 交AE的延长线于点F,则DF的长为.
17. 如图,在 中, , ,AD是 的中线,AE是 的角平分线, 交AE的延长线于点F,则DF的长为. 18. 如图,△ABC的周长是12,OB、OC分别平分∠ABC和∠ACB,OD⊥BC于D,且OD=3,则△ABC的面积是 .
18. 如图,△ABC的周长是12,OB、OC分别平分∠ABC和∠ACB,OD⊥BC于D,且OD=3,则△ABC的面积是 .
三、解答题
-
19. 如图, , , ,垂足分别为 , , .
求证: .
 20.(1)、如图1,利用网格线,作出三角形关于直线l的对称图形.
20.(1)、如图1,利用网格线,作出三角形关于直线l的对称图形. (2)、如图2,利用网格线,在BC上找一点P,使点P到AB和AC的距离相等.
(2)、如图2,利用网格线,在BC上找一点P,使点P到AB和AC的距离相等. 21. 下面是胡老师带领学生,探究SSA是否能判定两个三角形全等的过程,请完成下列填空.
21. 下面是胡老师带领学生,探究SSA是否能判定两个三角形全等的过程,请完成下列填空.
如图:已知 ,在 和 中, , (公共边), , , , , 则 和 满足两边及一边的对角分别相等,即满足 , 很显然: ,(填“全等于”或“不全等于”)下结论:SSA(填“能”或“不能”)判定两个三角形全等.
22. 一副三角尺如图所示摆放,以AC为一边,在△ABC外作∠CAF=∠DCE,边AF交DC的延长线于点F,求∠F的度数. 23. 如图,已知CE⊥AB于E,BF⊥AC于F,BF交CE于D点,且AB=AC
23. 如图,已知CE⊥AB于E,BF⊥AC于F,BF交CE于D点,且AB=AC (1)、求证:△ABF≌△ACE.(2)、求证:A点在∠EDF的平分线上.24. 如图所示,在 中, , , 于点D, ,DG交BC于点G,点E在BC的延长线上,且 .
(1)、求证:△ABF≌△ACE.(2)、求证:A点在∠EDF的平分线上.24. 如图所示,在 中, , , 于点D, ,DG交BC于点G,点E在BC的延长线上,且 . (1)、求 和 的度数;(2)、写出图中所有等腰三角形(不必证明).
(1)、求 和 的度数;(2)、写出图中所有等腰三角形(不必证明).

