广西壮族自治区玉林市北流市2019-2020学年八年级上学期数学期中考试试卷
试卷更新日期:2019-12-24 类型:期中考试
一、单选题
-
1. 下列图案中,是利用轴对称设计的图案的有( )A、
 B、
B、 C、
C、 D、
D、 2. 下列长度的三条线段,能组成三角形的是( )A、 B、 C、 D、3. 如图,是一块三角形木板的残余部分,量得 , ,这块三角形木板缺少的角是( )
2. 下列长度的三条线段,能组成三角形的是( )A、 B、 C、 D、3. 如图,是一块三角形木板的残余部分,量得 , ,这块三角形木板缺少的角是( ) A、 B、 C、 D、4. 如图,直线 , , ,则 的度数为( )
A、 B、 C、 D、4. 如图,直线 , , ,则 的度数为( ) A、 B、 C、 D、5. 下列度数不能成为某多边形的内角和的是( )A、 B、 C、 D、6. 根据下列条件,能画出唯一的三角形 的是( )A、 , , B、 , , C、 , , D、 , ,7. 如图所示,表示三条相互交叉的公路,现要建一个货物中转站,要求它到三条公路的距离相等,则可供选择的地址有( )
A、 B、 C、 D、5. 下列度数不能成为某多边形的内角和的是( )A、 B、 C、 D、6. 根据下列条件,能画出唯一的三角形 的是( )A、 , , B、 , , C、 , , D、 , ,7. 如图所示,表示三条相互交叉的公路,现要建一个货物中转站,要求它到三条公路的距离相等,则可供选择的地址有( ) A、1处 B、2处 C、3处 D、4处8. 点 和点 关于 轴对称,则点 、 两点间的距离为( )A、0 B、4 C、 D、69. 如图,在 中, , 平分 , 垂直平分 , , ,则 的长为( )
A、1处 B、2处 C、3处 D、4处8. 点 和点 关于 轴对称,则点 、 两点间的距离为( )A、0 B、4 C、 D、69. 如图,在 中, , 平分 , 垂直平分 , , ,则 的长为( ) A、5 B、6 C、10 D、1210. 如图, 周长为 ,把 的边 对折,使顶点 和点 重合,折痕交 边于点 ,交 边于点 ,连接 ,若 ,则 的周长是( )
A、5 B、6 C、10 D、1210. 如图, 周长为 ,把 的边 对折,使顶点 和点 重合,折痕交 边于点 ,交 边于点 ,连接 ,若 ,则 的周长是( ) A、 B、 C、 D、11. 如图,七边形 中, 、 的延长线相交于点 ,若图中 、 、 、 的外角和为 ,则 的度数为( )
A、 B、 C、 D、11. 如图,七边形 中, 、 的延长线相交于点 ,若图中 、 、 、 的外角和为 ,则 的度数为( ) A、 B、 C、 D、12. 如图, 是 的角平分线, ,垂足为 , , 和 的面积分别是60和40,则 的面积( )
A、 B、 C、 D、12. 如图, 是 的角平分线, ,垂足为 , , 和 的面积分别是60和40,则 的面积( ) A、8 B、10 C、12 D、20
A、8 B、10 C、12 D、20二、填空题
-
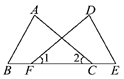
13. 三角形具有稳定性,要使一个四边形框架稳定不变形,至少需要钉根木条.14. 一个正多边形的每个外角都是36°,这个正多边形的边数是 .15. 如图所示,F、C在线段BE上,且∠1=∠2,BC=EF.若要根据“SAS”使△ABC≌△DEF,还需要补充的条件是.
 16. 如图, 中, 、 、 、 分别是边 、 、 、 的中点,若 ,则 .
16. 如图, 中, 、 、 、 分别是边 、 、 、 的中点,若 ,则 . 17. 如图,在 中, , , 的平分线与 的外角平分线交于点 ,连接 ,则 的度数为.
17. 如图,在 中, , , 的平分线与 的外角平分线交于点 ,连接 ,则 的度数为. 18. 如图,在平面直角坐标系中,将直角三角形的直角顶点放在点 处,两直角边分别与坐标轴交于点 和点 ,则 的值为.
18. 如图,在平面直角坐标系中,将直角三角形的直角顶点放在点 处,两直角边分别与坐标轴交于点 和点 ,则 的值为.
三、解答题
-
19. 如图,求作一点P,使 ,且使点P到 两边的距离相等(利用尺规作图、不写作法,保留作图痕迹)
 20. 如图,小明从点A出发,前进10m后向右转20°,再前进10m后又向右转20°,这样一直下去,直到他第一次回到出发点A为止,他所走的路径构成了一个多边形.
20. 如图,小明从点A出发,前进10m后向右转20°,再前进10m后又向右转20°,这样一直下去,直到他第一次回到出发点A为止,他所走的路径构成了一个多边形.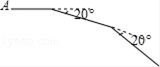 (1)、小明一共走了多少米?(2)、这个多边形的内角和是多少度?21. 如图,在 中, , 是 边上的高, , , .求:
(1)、小明一共走了多少米?(2)、这个多边形的内角和是多少度?21. 如图,在 中, , 是 边上的高, , , .求: (1)、 的面积.(2)、 的长.22. 如图,已知AB=AC,AD=AE,BD=CE,求证:∠3=∠1+∠2.
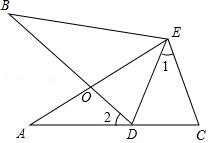
(1)、 的面积.(2)、 的长.22. 如图,已知AB=AC,AD=AE,BD=CE,求证:∠3=∠1+∠2. 23. 如图,∠A=∠B,AE=BE,点D在AC边上,∠1=∠2,AE和BD相交于点O.
23. 如图,∠A=∠B,AE=BE,点D在AC边上,∠1=∠2,AE和BD相交于点O.求证:△AEC≌△BED;