广西壮族自治区贵港市港南区2019-2020学年八年级上学期数学期中考试试卷
试卷更新日期:2019-12-24 类型:期中考试
一、单选题
-
1. 下列运算结果最大的是( )A、 B、 C、 D、2. 化简 的结果是( )
A、 B、 C、 D、3. 下列运算正确的是( )A、 B、(2ab)2÷a2b=4ab C、2ab 3a=6a2b D、(a﹣1)(1﹣a)=a2﹣14. 把分式 中的x和y都扩大2倍,则分式的值( )A、扩大4倍 B、扩大2倍 C、缩小2倍 D、不变5. 化简 的结果是( )A、 B、 C、 D、6. 已知a、b、c是△ABC的三条边长,化简|a+b-c|-|c-a-b|的结果为( )A、2a+2b-2c B、2a+2b C、2c D、07. 关于x的分式方程 有增根,则a的值为( )A、2 B、3 C、4 D、58. 小芳有两根长度为 和 的木条,她想钉一个三角形木框,桌上有下列长度的几根木条,她应该选择木条的长度为( )A、 B、 C、 D、9. 如图,在 中, , , 是 上一点,将 沿 折叠,使 点落在 边上的 处,则 等于( )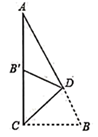 A、 B、 C、 D、10. 如图所示,AB=AC,AD=AE,∠BAC=∠DAE,∠1=25°,∠2=30°,则∠3=( )
A、 B、 C、 D、10. 如图所示,AB=AC,AD=AE,∠BAC=∠DAE,∠1=25°,∠2=30°,则∠3=( )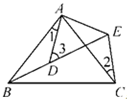 A、60° B、55° C、50° D、无法计算11. 如图, 的面积为24, 是 边的中线, 为 的中点,则 的面积为( )
A、60° B、55° C、50° D、无法计算11. 如图, 的面积为24, 是 边的中线, 为 的中点,则 的面积为( )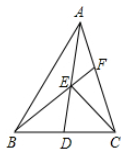 A、5 B、6 C、7 D、812. 如图, 中, , 于 , 平分 ,且 于 ,与 相交于点 , 于 ,交 于 ,下列结论:① ;② ;③ ;④ .其中正确的是( )
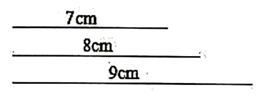
A、5 B、6 C、7 D、812. 如图, 中, , 于 , 平分 ,且 于 ,与 相交于点 , 于 ,交 于 ,下列结论:① ;② ;③ ;④ .其中正确的是( )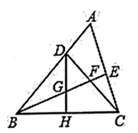 A、①② B、①③ C、①②③ D、①②③④
A、①② B、①③ C、①②③ D、①②③④二、填空题
-
13. 若分式 值为0,则 .14. 已知 ,则 的值等于.15. 如图,在 中, 垂直平分 ,若 的周长是12, ,则 的长.
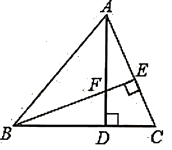
 16. 已知如图,∠B=∠C=90°,E是BC的中点,DE平分∠ADC,∠CED=35°,则∠EAB是度.
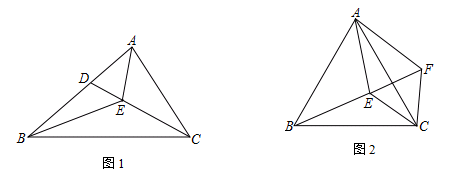
16. 已知如图,∠B=∠C=90°,E是BC的中点,DE平分∠ADC,∠CED=35°,则∠EAB是度.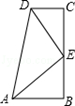 17. 如图,△ABC是边长为3的等边三角形,△BDC是等腰三角形,且∠BDC=120°.以D为顶点作一个60°角,使其两边分别交AB于点M,交AC于点N,连接MN,则△AMN的周长为.
17. 如图,△ABC是边长为3的等边三角形,△BDC是等腰三角形,且∠BDC=120°.以D为顶点作一个60°角,使其两边分别交AB于点M,交AC于点N,连接MN,则△AMN的周长为.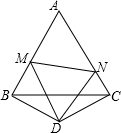 18. 已知:如图,BD为△ABC的角平分线,且BD=BC,E为BD延长线上的一点,BE=BA,过E作EF⊥AB,F为垂足,下列结论:①△ABD≌△EBC;②∠BCE+∠BCD=180°;③AD=EF=EC;④AE=EC,其中正确的是(填序号)
18. 已知:如图,BD为△ABC的角平分线,且BD=BC,E为BD延长线上的一点,BE=BA,过E作EF⊥AB,F为垂足,下列结论:①△ABD≌△EBC;②∠BCE+∠BCD=180°;③AD=EF=EC;④AE=EC,其中正确的是(填序号)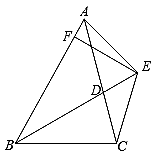
三、解答题
-
19.(1)、解方程: .(2)、在 中, 比 大 , 比 小 ,求 的各内角的度数.20. 已知 为 的内角平分线, , , ,请画出图形,(必须保留作图痕迹).
 21. 如图,点 , 在 的边 上, , ,求证: .
21. 如图,点 , 在 的边 上, , ,求证: .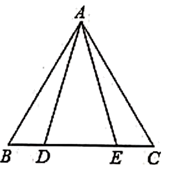 22. “绿水青山就是金山银山”,为了进一步优化河道环境,甲乙两工程队承担河道整治任务,甲、乙两个工程队每天共整治河道1500米,甲工程队整治3600米所用的时间与乙工程队整治2400米所用时间相等。甲工程队每天整治河道多少米?
22. “绿水青山就是金山银山”,为了进一步优化河道环境,甲乙两工程队承担河道整治任务,甲、乙两个工程队每天共整治河道1500米,甲工程队整治3600米所用的时间与乙工程队整治2400米所用时间相等。甲工程队每天整治河道多少米?