人教版初中数学2019-2020学年八年级上学期期末专题复习专题5：等腰三角形

试卷更新日期：2019-12-23 类型：复习试卷

进入出卷网下载

一、单选题

1. △ABC中，AB=AC，∠A=∠C，则△ABC是（）

A、等腰三角形 B、等边三角形 C、不等边三角形 D、不能确定

查看试题解析
2. 已知∠AOB＝30°，点P在∠AOB的内部，点P₁和点P关于OA对称，点P₂和点P关于OB对称，则P₁、O、P₂三点构成的三角形是（）

A、直角三角形 B、钝角三角形 C、等腰直角三角形 D、等边三角形

查看试题解析
3. 如图，△ABC中，AB=AC，BD平分∠ABC交AC于G，DM∥BC交∠ABC的外角平分线于M，交AB，AC于F，E，以下结论：①MB⊥BD，②FD=EC，③EC=EF+DG，④CE=MD/2，其中一定正确的有（）

A、1个 B、2个 C、3个 D、4个

查看试题解析
4. 如图，在△ABC 中，∠BAC＝72°，∠C＝36°，∠BAC 的平分线 AD 交 BC 于 D，则图中有等腰三角形（）

A、0 个 B、1 个 C、2 个 D、3 个

查看试题解析

二、填空题

5. 如图，在 $△ A B C$ 中， $A B = A C$ ， $B F = C D$ ， $B D = C E$ ， $∠ F D E = α$ 与 $∠ A$ 的关系是.

查看试题解析
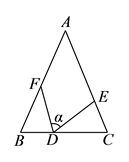6. 如图，D是AB边上的中点，将△ABC沿过D的直线折叠，使点A落在BC上F处，若∠B=50°，则∠BDF=度.

查看试题解析
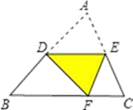7. 如图，等腰三角形ABC底边BC的长为 4cm，面积是12cm² ，腰 AB的垂直平分线EF交AC于点F，若 D为 BC边上的中点，M为线段EF上一动点，则△BDM的周长最短为cm.

查看试题解析
8. 如图，等边△ABC边长为10，P在AB上，Q在BC延长线，CQ＝PA ，过点P作PE⊥AC点E ，过点P作PF∥BQ ，交AC边于点F ，连接PQ交AC于点D ，则DE的长为．

查看试题解析

三、综合题

9. 如果三角形有一边上的中线恰好等于这边的长，那么我们称这个三角形为“美丽三角形”，

(1)、如图△ABC中，AB=AC= $\sqrt{5}$ ，BC=2，求证：△ABC是“美丽三角形”；

(2)、在Rt△ABC中，∠C=90°，AC=2 $\sqrt{3}$ ，若△ABC是“美丽三角形”，求BC的长.

查看试题解析
10. 图1、图2中，点B为线段AE上一点，△ABC与△BED都是等边三角形.

(1)、如图1，求证：AD=CE.

(2)、如图2，设CE与AD交于点F，连接BF.
①求证：∠CFA=60°.

②求证：CF+BF=AF.

查看试题解析
11. 如图，D是等边三角形ABC内一点，将线段AD绕点A顺时针旋转60°，得到线段AE，连接CD，BE．

(1)、求证：∠AEB=∠ADC；

(2)、连接DE，若∠ADC=105°，求∠BED的度数．

查看试题解析