人教版初中数学2019-2020学年九年级上学期期末专题复习 专题5：旋转与中心对称

试卷更新日期：2019-12-23 类型：复习试卷

进入 出卷网 下载

一、单选题

  • 1. 在学习图案与设计这一节课时，老师要求同学们利用图形变化设计图案，下列设计的图案中是中心对称图形但是不是轴对称图形的是（     ）
    A、 B、 C、 D、

    查看试题解析

  • 2. 如图所示是一个旋转对称图形，若将它绕自身中心旋转一定角度之后不能与原图重合，则这个角度可能是 (    )

    A、60° B、90° C、120° D、180°

    查看试题解析

  • 3. 若点A（x，3）与点B（2，y）关于原点对称，则（   ）
    A、x=﹣2，y=﹣3 B、x=2，y=3 C、x=﹣2，y=3 D、x=2，y=﹣3

    查看试题解析

  • 4. 如图，在平面直角坐标系xOy中，已知点A（3，4），将OA绕坐标原点O逆时针旋转90°至OA′，则点A′的坐标是（   ）

    ．

    A、（-4，3） B、（-3，4） C、（3，-4） D、（4，-3）

    查看试题解析

二、填空题

  • 5. 如图1，一艺术拱门由两部分组成，下部为矩形ABCD，AB，AD的长分别是2 3 m和4m，上部是圆心为0的劣弧CD，圆心角∠COD=120°．现欲以B点为支点将拱门放倒；放倒过程中矩形ABCD所在的平面始终与地面垂直，如图2、图3、图4所示记拱门上的点到地面的最大距离hm，则h的最大值为m。

    查看试题解析

  • 6. 如图，三角形ABC绕点A逆时针旋转90°到三角形AB'C'的位置．已知∠BAC=36°，则∠B'AC= 度。

    查看试题解析

  • 7. 如图，在△ABC中，∠CAB=75°，在同一平面内，将△ABC绕点A旋转到△AB'C'的位置，使得CC'∥AB，则∠BAB'=。

    查看试题解析

三、解答题

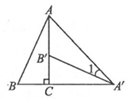
  • 8. 如图，将Rt△ABC绕直角顶点C顺时针旋转90°，得到△A′B'C，连接AA'，若∠1= 20°，求∠B的度数.

    查看试题解析

四、作图题

  • 9. 已知，已知A（-1，-1），B（-3，3），C（-4，1）.

    ①画出 ΔABC 关于原点O的对称的 ΔA1B1C1 并写出A的对应点 A1 的坐标；

    ②画出 ΔABC 绕点O按顺时针方向旋转90°后的 ΔA2B2C2 ，并写出A的对应点 A2 的坐标.

    查看试题解析

  • 10. △ABC在平面直角坐标系xOy中的位置如图所示．

    (1)、作△ABC关于点C成中心对称的△A1B1C1 ．
    (2)、将△A1B1C1向右平移4个单位，作出平移后的△A2B2C2 ．
    (3)、在x轴上求作一点P，使PA1+PC2的值最小，并写出点P的坐标（不写解答过程，直接写出结果）

    查看试题解析

  • 11. 如图是由边长为1个单位长度的小正方形组成的网格，线段AB的端点在格点上。

    (1)、将线段BA绕点B逆时针旋转90°得线段BC，画出BC；建立适当的平面直角坐标系xOy，使得B点的坐标为(-1，2)，在此坐标系下，C点的坐标为；
    (2)、在第(1)题的坐标系下，二次函数y=ax2+bx+c的图象过O、B、C三点，试求出抛物线解析式。

    查看试题解析