人教版初中数学2019-2020学年九年级上学期期末专题复习专题3：二次函数与一元二次方程

试卷更新日期：2019-12-23 类型：复习试卷

进入出卷网下载

一、单选题

1. 已知，二次函数y=ax²+bx+c(a≠0)，下表列出了该函数的x，y的部分对应值：

x

…

-2

-1

0

1

2

3

…

y

…

4

5

4

1

-4

-11

请根据表中信息回答问题：一元二次方程ax²+bx+c+11=0的解是（）

A、x₁=2，x₂=-3 B、x₁=-5，x₂=-3 C、x₁=-4，x₂=3 D、x₁=-5，x₂=3

查看试题解析
2. 已知函数 $y = 3 - (x - m) (x - n)$ ，并且 $a$ ， $b$ 是方程 $3 - (x - m) (x - n) = 0$ 的两个根，则实数 $m$ ， $n$ ， $a$ ， $b$ 的大小关系可能是（）

A、 $m < n < b < a$ B、 $m < a < n < b$ C、 $a < m < b < n$ D、 $a < m < n < b$

查看试题解析
3. 二次函数y=x²+bx的图象如图，对称轴为直线x=1，若关于x的一元二次方程x²+bx﹣t=0（t为实数）在﹣1＜x＜4的范围内有解，则t的取值范围是（）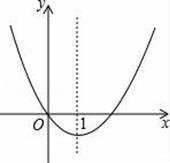

A、t≥﹣1 B、﹣1≤t＜3 C、3＜t＜8 D、﹣1≤t＜8

查看试题解析
4. 如表是满足二次函数 $y = a x^{2} + b x + c$ 的五组数据， $x_{1}$ 是方程 $a x^{2} + b x + c = 0$ 的一个解，则下列选项中正确的是（）

A、 $1 . 6< x_{1} <1 .8$ B、 $2.0 < x_{1} < 2.2$ C、 $1. 8 < x_{1} < 2.0$ D、 $2.2 < x_{1} < 2.4$

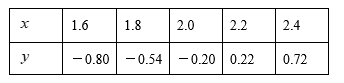查看试题解析
5. 如图，二次函数y＝ax²+bx+c（a≠0）的图象过点（﹣2，0），对称轴为直线x＝1.有以下结论：①abc＞0；②8a+c＞0；③若A（x₁ ， m），B（x₂ ， m）是抛物线上的两点，当x＝x₁+x₂时，y＝c；④点M，N是抛物线与x轴的两个交点，若在x轴下方的抛物线上存在一点P，使得PM⊥PN，则a的取值范围为a≥1；⑤若方程a（x+2）（4﹣x）＝﹣2的两根为x₁ ， x₂ ，且x₁＜x₂ ，则﹣2≤x₁＜x₂＜4.其中结论正确的有（）

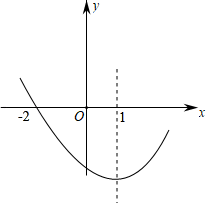A、2个 B、3个 C、4个 D、5个

查看试题解析

二、填空题

6. 对任意实数 $a$ ，若多项式 $2 b^{2} ﹣ 5 a b + 3 a^{2}$ 的值总大于 $﹣ 3$ ，则实数 $b$ 的取值范围是．

查看试题解析
7. 抛物线y＝ax²＋bx＋c经过点A(－3，0)、B(4，0)两点，则关于x的一元二次方程a(x－1)²＋c＝b－bx的解是

查看试题解析

三、解答题

8. 如图，在平面直角坐标系中，抛物线y=ax²+3与y轴交于点A ，过点A与x轴平行的直线交抛物线 $y = \frac{1}{3} x^{2}$ 于点B、C ，求BC的长.

查看试题解析

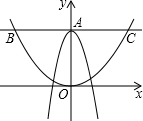
四、综合题

9. 已知关于 $x$ 的一元二次方程 $x^{2} - 3 x + k - 1 = 0$ 有实数根， $k$ 为正整数.

(1)、求 $k$ 的值；

(2)、当此方程有两个不为0的整数根时，将关于 $x$ 的二次函数 $y = x^{2} - 3 x + k - 1$ 的图象向下平移2个单位，求平移后的函数图象的解析式；

(3)、在（2）的条件下，将平移后的二次函数图象位于 $y$ 轴左侧的部分沿 $x$ 轴翻折，图象的其余部分保持不变，得到一个新的图象G.当直线 $y = 5 x + b$ 与图象G有3个公共点时，请你直接写出 $b$ 的取值范围.

查看试题解析
10. 二次函数y=ax²＋bx＋c(a≠0)的图象如图所示，根据图象解答下列问题.

(1)、写出方程ax²＋bx＋c＝0的两个根；

(2)、写出不等式ax²＋bx＋c＞0的解集；

(3)、写出y随x的增大而减小的自变量x的取值范围；

(4)、若方程ax²＋bx＋c＝k有两个不相等的实数根，求k的取值范围.

查看试题解析
11. 二次函数y＝ax²＋bx＋c的图象如图所示，根据图象解答下列问题：

(1)、直接写出方程ax²＋bx＋c＝0的两个根；

(2)、直接写出y随 $x$ 的增大而减小的自变量x的取值范围；

(3)、若方程ax²＋bx＋c＝k有两个不相等的实数根，直接写出k的取值范围.

查看试题解析
12. 若二次函数 $y = a x^{2} + b x + c (a \neq 0)$ 图象的顶点在一次函数 $y = k x + t (k \neq 0)$ 的图象上，则称 $y = a x^{2} + b x + c (a \neq 0)$ 为 $y = k x + t (k \neq 0)$ 的伴随函数，如： $y = x^{2} + 1$ 是 $y = x + 1$ 的伴随函数.

(1)、若 $y = x^{2} - 4$ 是 $y = - x + p$ 的伴随函数，求直线 $y = - x + p$ 与两坐标轴围成的三角形的面积；

(2)、若函数 $y = m x - 3 (m \neq 0)$ 的伴随函数 $y = x^{2} + 2 x + n$ 与 $x$ 轴两个交点间的距离为4，求 $m$ ， $n$ 的值.

查看试题解析

x	…	-2	-1	0	1	2	3	…
y	…	4	5	4	1	-4	-11

人教版初中数学2019-2020学年九年级上学期期末专题复习 专题3：二次函数与一元二次方程

一、单选题

二、填空题

三、解答题

四、综合题

人教版初中数学2019-2020学年九年级上学期期末专题复习专题3：二次函数与一元二次方程