安徽省示范高中2019-2020学年高二上学期数学第二次考试试卷
试卷更新日期:2019-12-23 类型:月考试卷
一、单选题
-
1. 不等式 的解集为( )A、 B、 C、 D、2. 直线 的倾斜角是( )A、 B、 C、 D、3. 已知圆柱的轴截面为正方形,且圆柱的体积为 ,则该圆柱的侧面积为( )A、 B、 C、 D、4. 某公司在甲、乙、丙、丁四个地区分别有150,120,180,150个销售点.公司为了调查产品销售情况,需从这600个销售点中抽取一个容量为100的样本.按照分层抽样的方法抽取样本,则丙地区抽取的销售点比乙地区抽取的销售点多( )A、5个 B、8个 C、10个 D、12个5. 设 , 为两个不同的平面, , 为两条不同的直线,则下列判断正确的是( )A、若 , ,则 B、若 , ,则 C、若 , , ,则 D、若 , ,则6. 设 , , 分别为 内角 , , 的对边. 已知 ,则 ( )A、 B、1 C、 D、27. 在三棱柱 中, ( )A、 B、 C、 D、8. 把边长为2的正 沿 边上的高线 折成直二面角,则点 到 的距离是( )A、1 B、 C、 D、9. 某校从高一(1)班和(2)班的某次数学考试(试卷满分为100分)的成绩中各随机抽取了6份数学成绩组成一个样本,如茎叶图所示.若分别从(1)班、(2)班的样本中各取一份,则(2)班成绩更好的概率为( )
 A、 B、 C、 D、10. 在四面体 中, , , ,则四面体 外接球的表面积是( )A、 B、 C、 D、11. 已知 ,且 ,则 的取值范围是( )A、 B、 C、 D、
A、 B、 C、 D、10. 在四面体 中, , , ,则四面体 外接球的表面积是( )A、 B、 C、 D、11. 已知 ,且 ,则 的取值范围是( )A、 B、 C、 D、二、多选题
-
12. 如图,正方形 中, 分别是 的中点将 分别沿 折起,使 重合于点 .则下列结论正确的是( )
 A、 B、平面 C、二面角 的余弦值为 D、点 在平面 上的投影是 的外心
A、 B、平面 C、二面角 的余弦值为 D、点 在平面 上的投影是 的外心三、填空题
-
13. 已知等比数列 满足 , ,则公比 .14. 如图, 平面 , 为正方形,且 , , 分别是线段 , 的中点,则异面直线 与 所成角的余弦值为 .
 15. 在四棱锥 中,底面 为正方形, 底面 ,且 . 为棱 上的动点,若 的最小值为 ,则 .16. 为了了解某地高一学生的体能状况,某校抽取部分学生进行一分钟跳绳次数测试,将所得数据整理后,画出频率分布直方图(如图),则 , 估计该地学生跳绳次数的中位数是.
15. 在四棱锥 中,底面 为正方形, 底面 ,且 . 为棱 上的动点,若 的最小值为 ,则 .16. 为了了解某地高一学生的体能状况,某校抽取部分学生进行一分钟跳绳次数测试,将所得数据整理后,画出频率分布直方图(如图),则 , 估计该地学生跳绳次数的中位数是.
四、解答题
-
17. 已知正方体 , 是底 对角线的交点.求证:
 (1)、 面 ;(2)、 面 .18. 已知等差数列 的前三项分别为 ,1, .(1)、求 的通项公式;(2)、若 ,求数列 的前 项和 .19. 如图,在三棱柱 中, , , , 平面 .
(1)、 面 ;(2)、 面 .18. 已知等差数列 的前三项分别为 ,1, .(1)、求 的通项公式;(2)、若 ,求数列 的前 项和 .19. 如图,在三棱柱 中, , , , 平面 .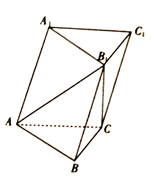 (1)、证明: 平面 ;(2)、求点 到平面 的距离.
(1)、证明: 平面 ;(2)、求点 到平面 的距离.
-


