江西省宜春市2016-2017学年七年级下学期期末考试数学试题
试卷更新日期:2017-07-28 类型:期末考试
一、选择题
-
1. 下列图形可由平移得到的是( )A、
 B、
B、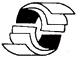 C、
C、 D、
D、 2. 下列调查中,最适宜采用全面调查方式的是( )A、对宜春市中学生每天学习所用时间的调查 B、对全国中学生心理健康现状的调查 C、对某班学生进行6月5日是“世界环境日”知晓情况的调查 D、对宜春市初中学生视力情况的调查3.
2. 下列调查中,最适宜采用全面调查方式的是( )A、对宜春市中学生每天学习所用时间的调查 B、对全国中学生心理健康现状的调查 C、对某班学生进行6月5日是“世界环境日”知晓情况的调查 D、对宜春市初中学生视力情况的调查3.下列实数中: 、 、 、 、0.1010010001…(往后每两个1之间依次多一个0)、
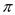 ,无理数有( )A、2个 B、3个 C、4个 D、5个4. 已知 是二元一次方程 的一组解,则 的值为( )A、 B、2 C、 D、5. 若关于 的不等式组 有解,则 的取值范围是( )A、 B、 C、 D、6. 在平面直角坐标系 中,对于点 ,我们把点 叫做点 伴随点.已知点 的伴随点为 ,点 的伴随点为 ,点 的伴随点为 ,…,这样依次得到点 , , ,…, ,….若点 的坐标为(2,4),点 的坐标为 ( )A、(-3,3) B、(-2,-2) C、(3,-1) D、(2,4)
,无理数有( )A、2个 B、3个 C、4个 D、5个4. 已知 是二元一次方程 的一组解,则 的值为( )A、 B、2 C、 D、5. 若关于 的不等式组 有解,则 的取值范围是( )A、 B、 C、 D、6. 在平面直角坐标系 中,对于点 ,我们把点 叫做点 伴随点.已知点 的伴随点为 ,点 的伴随点为 ,点 的伴随点为 ,…,这样依次得到点 , , ,…, ,….若点 的坐标为(2,4),点 的坐标为 ( )A、(-3,3) B、(-2,-2) C、(3,-1) D、(2,4)二、填空题
-
7. 的算术平方根是8. 在平面直角坐标系中,点 在第象限.9.
已知关于
 的二元一次方程组
的二元一次方程组 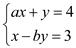 的解为
的解为 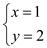 ,则
,则  10.
10.如图,将一副三角板和一张对边平行的纸条按下列方式摆放:含30°角的直角三角板的斜边与含45°角的直角三角板一直角边重合,含45°角的直角三角板的斜边与纸条一边重合,含30°角的三角板的一个顶点在纸条的另一边上,则∠1的度数是 .
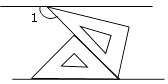 11. 关于 、 的二元一次方程组 的解满足不等式 ,则 的取值范围是12. 如果∠ 与∠ 的两条边分别平行,其中∠ = °;∠ = °,则∠ 的度数为
11. 关于 、 的二元一次方程组 的解满足不等式 ,则 的取值范围是12. 如果∠ 与∠ 的两条边分别平行,其中∠ = °;∠ = °,则∠ 的度数为
三、解答题。
-
13. 综合题
(1)、计算:
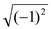 +
+ 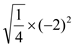 -
-  (2)、解方程组:14. 解不等式组: ,并将解集在数轴上表示出来.15. 已知 的算术平方根是3, 的立方根是2,求 的平方根.16.
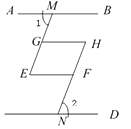
(2)、解方程组:14. 解不等式组: ,并将解集在数轴上表示出来.15. 已知 的算术平方根是3, 的立方根是2,求 的平方根.16.如图是一个汉字“互”字,其中, ∥ ,∠1=∠2,∠ =∠ .
求证:∠MEF=∠GHN
 17.
17.如图,三角形 经过平移后,使得点 与点 重合,使得点 与点 重合.
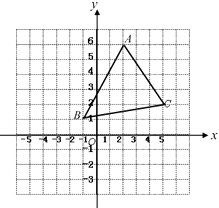 (1)、画出平移后的三角形 ;(2)、写出平移后的三角形 三个顶点的坐标 , , ;(3)、直接写出三角形 的面积为 .18.
(1)、画出平移后的三角形 ;(2)、写出平移后的三角形 三个顶点的坐标 , , ;(3)、直接写出三角形 的面积为 .18.某校为了了解初中学生在家做家务情况,随机抽取了该校部分初中生进行调查,依据相关数据绘制成以下不完整的统计图.
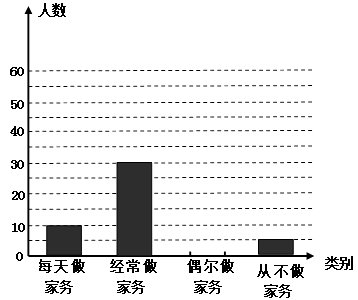
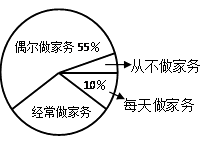
根据以上信息解答下列问题:
(1)、此次调查该校抽取的初中生人数名,“从不做家务”部分对应的扇形的圆心角度数为;
(2)、补全条形统计图;(3)、请估计该校2000名初中生中“经常做家务”的人数.19.对非负实数 “四舍五入”到个位的值记为 . 即当n为非负整数时,若 ,则 = . 如:
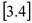 =3,
=3,  =4,…根据以上材料,解决下列问题:(1)、填空 = , =;(2)、
=4,…根据以上材料,解决下列问题:(1)、填空 = , =;(2)、若
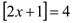 ,则 的取值范围是;(3)、求满足 的所有非负实数 的值.20. 为了倡导绿色出行,某市政府2016年投资了320万元,首期建成120个公共自行车站点,配置2500辆公共自行车,2017年又投资了104万元新建了40个公共自行车站点,配置800辆公共自行车. (注:从2016年起至2020年,每个站点的造价和公共自行车的单价每年都保持不变)(1)、请问每个站点的造价和公共自行车的单价分别是多少万元?(2)、若到2020年该市政府将再建造 个新公共自行车站点和配置 辆公共自行车,并且公共自行车数量不超过新公共自行车站点数量的23倍,并且再建造的新公共自行车站点不超过102个,市政府共有几种选择方案,哪种方案市政府投入的资金最少?21.
,则 的取值范围是;(3)、求满足 的所有非负实数 的值.20. 为了倡导绿色出行,某市政府2016年投资了320万元,首期建成120个公共自行车站点,配置2500辆公共自行车,2017年又投资了104万元新建了40个公共自行车站点,配置800辆公共自行车. (注:从2016年起至2020年,每个站点的造价和公共自行车的单价每年都保持不变)(1)、请问每个站点的造价和公共自行车的单价分别是多少万元?(2)、若到2020年该市政府将再建造 个新公共自行车站点和配置 辆公共自行车,并且公共自行车数量不超过新公共自行车站点数量的23倍,并且再建造的新公共自行车站点不超过102个,市政府共有几种选择方案,哪种方案市政府投入的资金最少?21.如图1,在平面直角坐标系中,点 为 轴负半轴上一点,点 为 轴正半轴上一点, , ,其中 , 满足关系式:
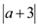 +
+ 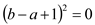 .
. (1)、= , = , △ 的面积为;(2)、如图2,若 ⊥ ,点 线段 上一点,连接 ,延长 交 于点 ,当∠ =∠ 时,求证: 平分∠ ;(3)、如图3,若 ⊥ ,点 是点 与点 之间一动点,连接 , 始终平分∠ ,当点 在点 与点 之间运动时, 的值是否变化?若不变,求出其值;若变化,请说明理由.
(1)、= , = , △ 的面积为;(2)、如图2,若 ⊥ ,点 线段 上一点,连接 ,延长 交 于点 ,当∠ =∠ 时,求证: 平分∠ ;(3)、如图3,若 ⊥ ,点 是点 与点 之间一动点,连接 , 始终平分∠ ,当点 在点 与点 之间运动时, 的值是否变化?若不变,求出其值;若变化,请说明理由.