吉林省长春市新区2018-2019学年九年级上学期数学期末考试试卷

试卷更新日期：2019-12-21 类型：期末考试

进入出卷网下载

一、单选题

1. 下列根式中，能与 $\sqrt{3}$ 合并的二次根式为（）

A、 $\sqrt{24}$ B、 $\sqrt{\frac{3}{2}}$ C、 $\sqrt{12}$ D、 $\sqrt{18}$

查看试题解析
2. 甲、乙两地的实际距离是20千米，在比例尺为1：500000的地图上甲乙两地的距离（　　）

A、40cm B、400cm C、0.4cm D、4cm

查看试题解析
3. 点(5，﹣2)关于x轴的对称点是(　　)

A、(5，﹣2) B、(5，2) C、(﹣5，2) D、(﹣5．﹣2)

查看试题解析
4. 一元二次方程 $x^{2} - 2 x + m = 0$ 总有实数根，则应满足的条件是（）

A、 $m > 1$ B、 $m = 1$ C、 $m < 1$ D、 $m \leq 1$

查看试题解析
5. 掷一枚质地均匀的硬币一次，则掷到正面朝上的概率等于（）

A、1 B、 $\frac{1}{2}$ C、 $\frac{1}{4}$ D、0

查看试题解析
6. 如图，△ABC的顶点是正方形网格的格点，则sinA是（　　）

A、 $\frac{\sqrt{2}}{3}$ B、 $\frac{\sqrt{5}}{5}$ C、 $\frac{2 \sqrt{5}}{5}$ D、 $\frac{1}{2}$

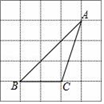查看试题解析
7. 某药品经过两次降价，每瓶零售价由 156 元降为 118 元．已知两次降价的百分率相同每次降价的百分率为 x，根据题意列方程得（）

A、156（1+x）²=118 B、156（1﹣x²）=118 C、156（1﹣2x）=118 D、156（1﹣x）²=118

查看试题解析
8. 如图，已知点A（12，0），O为坐标原点，P是线段OA上任一点（不含端点O、A），二次函数y₁的图象过P、O两点，二次函数y₂的图象过P、A两点，它们的开口均向下，顶点分别为B、C，射线OB与射线AC相交于点D．则当OD=AD=9时，这两个二次函数的最大值之和等于（　　）

A、8 B、3 $\sqrt{5}$ C、2 $\sqrt{7}$ D、6

查看试题解析

二、填空题

9. 计算：- $\sqrt{16}$ = ．

查看试题解析
10. 已知 $\frac{m - n}{n}$ ＝ $\frac{1}{2}$ ，则 $\frac{m}{n}$ 的值为．

查看试题解析
11. 关于x的方程x²﹣kx+2＝0有一个根是1，则k的值为．

查看试题解析
12. 如图，在△ABC中，点D、E分别在AB、AC边上，DE∥BC，若 $\frac{A D}{A B} = \frac{2}{3}$ ，AE=4，则EC等于．

查看试题解析
13. 如图，在平面直角坐标系中，已知正方形ABCD，点A（2，0），B（0，4），那么点C的坐标是.

查看试题解析
14. 在平面直角坐标系中，某二次函数图象的顶点坐标为（2，﹣1），此函数图象与x轴相交于P、Q两点，且PQ＝6，若此函数图象通过（1，a）、（3，b）、（﹣1，c）、（﹣3，d）四点，则a、b、c、d中为正值的是（选填“a”、“b”“c”或“d”）

查看试题解析

三、解答题

15. 计算：（ $\sqrt{12}$ + $\sqrt{8}$ ）× $\sqrt{3}$

查看试题解析
16. 计算：tan60°-cos45°•sin45°+sin30°．

查看试题解析
17. 解方程:

(1)、x²﹣x＝0

(2)、x²﹣2x﹣3＝0

查看试题解析
18. 张明和王华两人玩“剪刀、石头、布”的游戏，游戏规则为：剪刀胜布，布胜石头，石头胜剪刀．请用树状图（或列表）的方法，求王华胜出的概率．

查看试题解析
19. 某商店经销一种进价为每千克40元的水产品．据市场分析，若按每千克50元销售，一个月能售出500千克；销售单价每涨1元，月销售量就减少10千克．针对这种水产品的销售情况，请解答一下问题：

(1)、当销售单价定位每千克55元时，计算月销售量和月销售利润；

(2)、商店要使月销售利润为8000元，销售单价应定为多少？

查看试题解析
20. 如图，在一滑梯侧面示意图中，BD∥AF，BC⊥AF于点C，DE⊥AF于
点E．BC＝1.8m，BD＝0.5m，∠A＝45º，∠F＝29º．

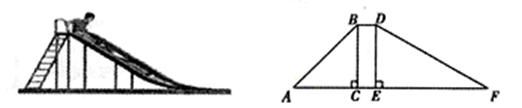(1)、求滑道DF的长(精确到0.1m)；

(2)、求踏梯AB底端A与滑道DF底端F的距离AF(精确到0.1m)．
(参考数据：sin29º≈0.48，cos29º≈0.87，tan29º≈0.55)

查看试题解析
21. 方格纸中每个小正方形的边长都是单位1，△OAB在平面直角坐标系中的位置如图所示，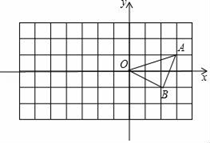

解答问题：

(1)、请按要求对△OAB作变换：以点O为位似中心，位似比为2：1，将△ABC在位似中心的异侧进行放大得到△OA′B′．

(2)、写出点A′的坐标；

(3)、求△OA′B'的面积．

查看试题解析
22. 感知：如图1，AD平分∠BAC．∠B+∠C=180°，∠B=90°，易知：DB=DC．

(1)、探究：如图2，AD平分∠BAC，∠ABD+∠ACD=180°，∠ABD＜90°，求证：DB=DC．

(2)、应用：如图3，四边形ABCD中，∠B=45°，∠C=135°，DB=DC=a，则AB﹣AC=（）（用含a的代数式表示）

查看试题解析
23. 已知：在Rt△ABC中，∠B＝90°，BC＝4cm ， AB＝8cm ， D、E、F分别为AB、AC、BC边上的中点．若P为AB边上的一个动点，PQ∥BC ，且交AC于点Q ，以PQ为一边，在点A的异侧作正方形PQMN ，记正方形PQMN与矩形EDBF的公共部分的面积为y ．

(1)、如图，当AP＝3cm时，求y的值；

(2)、设AP＝xcm ，试用含x的代数式表示y（cm²）；

(3)、当y＝2cm²时，试确定点P的位置．

查看试题解析
24. 如图，在平面直角坐标系中，抛物线y＝﹣x²+3x与x轴交于O、A两点，与直线y＝x交于O、B两点，点A、B的坐标分别为（3，0）、（2，2）．点P在抛物线上，且不与点O、B重合，过点P作y轴的平行线交射线OB于点Q ，以PQ为边作R△PQN ，点N与点B始终在PQ同侧，且PN＝1．设点P的横坐标为m（m＞0），PQ长度为d ．

(1)、用含m的代数式表示点P的坐标．

(2)、求d与m之间的函数关系式．

(3)、当△PQN是等腰直角三角形时，求m的值．

(4)、直接写出△PQN的边与抛物线有两个交点时m的取值范围．

查看试题解析