吉林省长春市南关区2018-2019学年九年级上学期数学期末考试试卷
试卷更新日期:2019-12-21 类型:期末考试
一、单选题
-
1. 计算 的结果是A、﹣3 B、3 C、﹣9 D、92. 下列各式中,与 是同类二次根式的是( )
A、 B、 C、 D、3. 用配方法解方程x2﹣4x﹣6=0,变形正确的是( )A、(x﹣2)2=2 B、(x﹣2)2=10 C、(x﹣4)2=22 D、(x+2)2=104. 我国古代数学《九章算术》中,有个“井深几何”问题:今有井径五尺,不知其深,立五尺木于井上,从木末望水岸,入径四寸(1尺=10寸),问井深几何?其意思如图所示,则井深BD的长为( ) A、12尺 B、56尺5寸 C、57尺5寸 D、62尺5寸5. 如图,在△ABC中,∠C=90°,AB=13,AC=12,下列三角函数表示正确的是( )
A、12尺 B、56尺5寸 C、57尺5寸 D、62尺5寸5. 如图,在△ABC中,∠C=90°,AB=13,AC=12,下列三角函数表示正确的是( ) A、 = B、 = C、 = D、 =6. 二次函数y=﹣2x2+bx+c的图象如图所示,则下列结论正确的是( )
A、 = B、 = C、 = D、 =6. 二次函数y=﹣2x2+bx+c的图象如图所示,则下列结论正确的是( ) A、b<0,c>0 B、b<0,c<0 C、b>0,c<0 D、b>0,c>07. 如图,在△ABC中,∠C=90°,∠B=30°,AC=3.若点P是BC边上任意一点,则AP的长不可能是( )
A、b<0,c>0 B、b<0,c<0 C、b>0,c<0 D、b>0,c>07. 如图,在△ABC中,∠C=90°,∠B=30°,AC=3.若点P是BC边上任意一点,则AP的长不可能是( ) A、7 B、5.3 C、4.8 D、3.58. 如图,在平面直角坐标系中,垂直于x轴的直线分别交抛物线y=x2(x≥0)和抛物线y= x2(x≥0)于点A和点B , 过点A作AC∥x轴交抛物线y= x2于点C , 过点B作BD∥x轴交抛物线y=x2于点D , 则 的值为( )
A、7 B、5.3 C、4.8 D、3.58. 如图,在平面直角坐标系中,垂直于x轴的直线分别交抛物线y=x2(x≥0)和抛物线y= x2(x≥0)于点A和点B , 过点A作AC∥x轴交抛物线y= x2于点C , 过点B作BD∥x轴交抛物线y=x2于点D , 则 的值为( )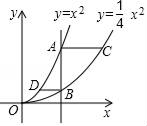 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
9. 计算: = .
10. 计算:cos245°+sin230°= .11. 关于 的一元二次方程 有两个不等实数根, 取值范围为.12. 如图,在△ABC中,∠ACB=90°,D是AB边的中点若AB=18,则CD的长为 .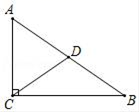 13. 如图,在△ABC中,点D在BC边上,△ABC∽△DBA . 若BD=4,DC=5,则AB的长为 .
13. 如图,在△ABC中,点D在BC边上,△ABC∽△DBA . 若BD=4,DC=5,则AB的长为 . 14. 如图,在平面直角坐标系中,抛物线y=﹣ (x﹣3)2+k经过坐标原点O,与x轴的另一个交点为A.过抛物线的顶点B分别作BC⊥x轴于C、BD⊥y轴于D,则图中阴影部分图形的面积和为 .
14. 如图,在平面直角坐标系中,抛物线y=﹣ (x﹣3)2+k经过坐标原点O,与x轴的另一个交点为A.过抛物线的顶点B分别作BC⊥x轴于C、BD⊥y轴于D,则图中阴影部分图形的面积和为 .
三、解答题
-
15. 计算: ﹣3 +2 .16. 解方程:3x2﹣4x﹣1=0.17. 一个不透明的袋子里装有三个分别标有数字﹣2、1、2的小球,除所标有的字不同外,其它方面均相同,现随机从中摸出一个小球,记录所摸出的小球上的数字后放回并搅匀,再随机摸出一个小球,记录小球上的数字.请用画树状图(或列表)的方法,求两次记录数字之和是正数的概率.18. 已知抛物线y=﹣2x2+bx+c经过点A(﹣1,﹣3)和点B(2,3)(1)、求这条抛物线所对应的函数表达式.(2)、点M(x1 , y1)、N(x2 , y2)在这条抛物线上,当1≤x2<x1时,比较y1与y2的大小.19. 图①、图②均是6×6的正方形网格,每个小正方形的顶点称为格点.线段AB的端点均在格点上,按下列要求画出图形.
 (1)、在图①中找到一个格点C , 使∠ABC是锐角,且tan∠ABC= ,并画出△ABC .(2)、在图②中找到一个格点D , 使∠ADB是锐角,且tan∠ADB=1,并画出△ABD .20. 如图,航拍无人机从A处测得一幢建筑物顶部B处的仰角为45°、底部C处的俯角为65°,此时航拍无人机A处与该建筑物的水平距离AD为80米.求该建筑物的高度BC(精确到1米).(参考数据:sin65°=0.91,cos65°=0.42,tan65°=2.14)
(1)、在图①中找到一个格点C , 使∠ABC是锐角,且tan∠ABC= ,并画出△ABC .(2)、在图②中找到一个格点D , 使∠ADB是锐角,且tan∠ADB=1,并画出△ABD .20. 如图,航拍无人机从A处测得一幢建筑物顶部B处的仰角为45°、底部C处的俯角为65°,此时航拍无人机A处与该建筑物的水平距离AD为80米.求该建筑物的高度BC(精确到1米).(参考数据:sin65°=0.91,cos65°=0.42,tan65°=2.14) 21. 现有一面12米长的墙,某农户计划用28米长的篱笆靠墙围成一个矩形养鸡场ABCD(篱笆只围AB、BC、CD三边),其示意图如图所示.
21. 现有一面12米长的墙,某农户计划用28米长的篱笆靠墙围成一个矩形养鸡场ABCD(篱笆只围AB、BC、CD三边),其示意图如图所示. (1)、若矩形养鸡场的面积为92平方米,求所用的墙长AD . (结果精确到0.1米)(参考数据: =1.41, =1.73, =2.24)(2)、求此矩形养鸡场的最大面积.22. 如图①所示,在△ABC中,点O是AC上一点,过点O的直线与AB,BC的延长线分别相交于点M,N.
(1)、若矩形养鸡场的面积为92平方米,求所用的墙长AD . (结果精确到0.1米)(参考数据: =1.41, =1.73, =2.24)(2)、求此矩形养鸡场的最大面积.22. 如图①所示,在△ABC中,点O是AC上一点,过点O的直线与AB,BC的延长线分别相交于点M,N.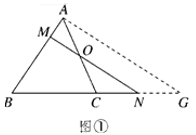 (1)、【问题引入】
(1)、【问题引入】若点O是AC的中点, ,求 的值;
温馨提示:过点A作MN的平行线交BN的延长线于点G.
(2)、【探索研究】若点O是AC上任意一点(不与A,C重合),求证: ;
(3)、【拓展应用】如图②所示,点P是△ABC内任意一点,射线AP,BP,CP分别交BC,AC,AB于点D,E,F.若 , ,求 的值.
 23. 如图,在△ABC中,∠C=90°,AC=BC,AB=8.点P从点A出发,以每秒2个单位长度的速度沿边AB向点B运动.过点P作PD⊥AB交折线AC﹣CB于点D,以PD为边在PD右侧做正方形PDEF.设正方形PDEF与△ABC重叠部分图形的面积为S,点P的运动时间为t秒(0<t<4).
23. 如图,在△ABC中,∠C=90°,AC=BC,AB=8.点P从点A出发,以每秒2个单位长度的速度沿边AB向点B运动.过点P作PD⊥AB交折线AC﹣CB于点D,以PD为边在PD右侧做正方形PDEF.设正方形PDEF与△ABC重叠部分图形的面积为S,点P的运动时间为t秒(0<t<4).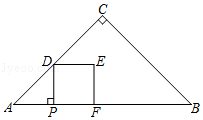 (1)、当点D在边AC上时,正方形PDEF的边长为(用含t的代数式表示).(2)、当点E落在边BC上时,求t的值.(3)、当点D在边AC上时,求S与t之间的函数关系式.(4)、作射线PE交边BC于点G,连结DF.当DF=4EG时,直接写出t的值.24. 如图,在平面直角坐标系中,直线y= +2分别交x轴、y轴于点A、B,抛物线y=﹣x2+bx+c经过点A、B.点P是x轴上一个动点,过点P作垂直于x轴的直线分别交抛物线和直线AB于点E和点F.设点P的横坐标为m.
(1)、当点D在边AC上时,正方形PDEF的边长为(用含t的代数式表示).(2)、当点E落在边BC上时,求t的值.(3)、当点D在边AC上时,求S与t之间的函数关系式.(4)、作射线PE交边BC于点G,连结DF.当DF=4EG时,直接写出t的值.24. 如图,在平面直角坐标系中,直线y= +2分别交x轴、y轴于点A、B,抛物线y=﹣x2+bx+c经过点A、B.点P是x轴上一个动点,过点P作垂直于x轴的直线分别交抛物线和直线AB于点E和点F.设点P的横坐标为m. (1)、点A的坐标为 .(2)、求这条抛物线所对应的函数表达式.(3)、点P在线段OA上时,若以B、E、F为顶点的三角形与△FPA相似,求m的值.(4)、若E、F、P三个点中恰有一点是其它两点所连线段的中点(三点重合除外),称E、F、P三点为“共谐点”.直接写出E、F、P三点成为“共谐点”时m的值.
(1)、点A的坐标为 .(2)、求这条抛物线所对应的函数表达式.(3)、点P在线段OA上时,若以B、E、F为顶点的三角形与△FPA相似,求m的值.(4)、若E、F、P三个点中恰有一点是其它两点所连线段的中点(三点重合除外),称E、F、P三点为“共谐点”.直接写出E、F、P三点成为“共谐点”时m的值.