吉林省长春市绿园区2018-2019学年九年级上学期数学期末考试试卷
试卷更新日期:2019-12-21 类型:期末考试
一、单选题
-
1. 计算 的结果是( )A、-3 B、3 C、 D、92. 计算 的值为()A、 B、 C、 D、3. 下列二次根式,最简二次根式是( )A、 B、 C、 D、4. 用配方法解下列方程,其中应在方程的左右两边同时加上4的是( )
A、 -2x=5 B、 +4x=5 C、 +2x=5 D、2 -4x=55. 一元二次方程4x2+1=3x的根的情况是( )
A、没有实数根 B、只有一个实数根 C、有两个相等的实数根 D、有两个不相等的实数根6. 如图所示,在等边三角形 中, 为 边上一点, 为 边上一点,且 , , ,则 的边长为( ) A、3 B、4 C、5 D、67. 如图,在6×6的正方形网格中,△ABC的顶点都在小正方形的顶点上,则tan∠BAC的值是( )
A、3 B、4 C、5 D、67. 如图,在6×6的正方形网格中,△ABC的顶点都在小正方形的顶点上,则tan∠BAC的值是( )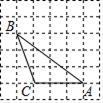 A、 B、 C、 D、8. 若二次函数 的图像如图所示,则下列结论正确的是( )
A、 B、 C、 D、8. 若二次函数 的图像如图所示,则下列结论正确的是( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
9. 计算:10. 计算;sin30° tan30°+cos60° tan60°= .11. 如图所示,在平面直角坐标系中, , ,则 点的坐标是 .
 12. 要把一根1m长的铜丝截成两段,用它们围成两个相似三角形,且相似比为 ,那么截成的两段铜丝的长度差应是m.13. 如图,在一场羽毛球比赛中,站在场内M处的运动员林丹把球从N点击到了对方内的B点,已知网高OA=1.52米,OB=4米,OM=5米,则林丹起跳后击球点N离地面的距离NM=米.
12. 要把一根1m长的铜丝截成两段,用它们围成两个相似三角形,且相似比为 ,那么截成的两段铜丝的长度差应是m.13. 如图,在一场羽毛球比赛中,站在场内M处的运动员林丹把球从N点击到了对方内的B点,已知网高OA=1.52米,OB=4米,OM=5米,则林丹起跳后击球点N离地面的距离NM=米.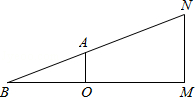 14. 如图,在平面直角坐标系中,抛物线 与抛物线 都经过 轴正半轴上的点 .过点 作 轴的平行线,分别与这两条抛物线交于 、 两点,以 为边向下作等边 ,则 的周长为 .
14. 如图,在平面直角坐标系中,抛物线 与抛物线 都经过 轴正半轴上的点 .过点 作 轴的平行线,分别与这两条抛物线交于 、 两点,以 为边向下作等边 ,则 的周长为 .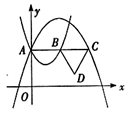
三、解答题
-
15. 解方程:16. 计算: .17. 如图是一副扑克牌的四张牌,将它们正面向下洗均匀,从中任意抽取两张牌,用画树状图(或列表)的方法,求抽出的两张牌中,牌面上的数字都是偶数的概率.
 18. 如图,△OAB的顶点坐标分别为O(0,0)、A(3,2)、B(2,0),将这三个顶点的坐标同时扩大到原来的2倍,得到对应点D、E、F.
18. 如图,△OAB的顶点坐标分别为O(0,0)、A(3,2)、B(2,0),将这三个顶点的坐标同时扩大到原来的2倍,得到对应点D、E、F. (1)、在图中画出△DEF;(2)、点E是否在直线OA上?为什么?(3)、△OAB与△DEF位似图形(填“是”或“不是”)19. 小明在解方程 时出现了错误,其解答过程如下:
(1)、在图中画出△DEF;(2)、点E是否在直线OA上?为什么?(3)、△OAB与△DEF位似图形(填“是”或“不是”)19. 小明在解方程 时出现了错误,其解答过程如下:解: (第一步)
(第二步)
(第三步)
(第四步)
(1)、小明解答过程是从第几步开始出错的,写出错误原因.(2)、请写出此题正确的解答过程.20. 小明在热气球A上看到正前方横跨河流两岸的大桥BC,并测得B、C两点的俯角分别为45°、35°.已知大桥BC与地面在同一水平面上,其长度为100m,求热气球离地面的高度.(结果保留整数)(参考数据:sin35°=0.57,cos35°=0.82,tan35°=0.70)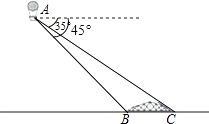 21. 小明同学说自己发现了判断一类方程有无实数根的一种简易方法:若一元二次方程a 的系数a、c异号(即两数为一正一负),那么这个方程一定有两个不相等的实数根.他的发现正确吗?请你先举实例验证一下是否正确,若你认为他的发现是一般规律,请加以证明.22.(1)、探究:如图①,直线 ,点 在 上,以点 为直角顶点作 ,角的两边分别交 与 于点 、 ,连结 .过点 作 于点 ,延长 交 于点 .
21. 小明同学说自己发现了判断一类方程有无实数根的一种简易方法:若一元二次方程a 的系数a、c异号(即两数为一正一负),那么这个方程一定有两个不相等的实数根.他的发现正确吗?请你先举实例验证一下是否正确,若你认为他的发现是一般规律,请加以证明.22.(1)、探究:如图①,直线 ,点 在 上,以点 为直角顶点作 ,角的两边分别交 与 于点 、 ,连结 .过点 作 于点 ,延长 交 于点 .
求证: .
(2)、应用:如图②,在图1的基础上,设 与 的交点为 ,若 , 与 之间的距离为2, 与 之间的距离为1,求 的长度. 23. 如图,在平面直角坐标系中,直线 分别交 轴、 轴于点 、 .点 的坐标是 ,抛物线 经过 、 两点且交 轴于点 .点 为 轴上一点,过点 作 轴的垂线交直线 于点 ,交抛物线于点 ,连结 ,设点 的横坐标为 .
23. 如图,在平面直角坐标系中,直线 分别交 轴、 轴于点 、 .点 的坐标是 ,抛物线 经过 、 两点且交 轴于点 .点 为 轴上一点,过点 作 轴的垂线交直线 于点 ,交抛物线于点 ,连结 ,设点 的横坐标为 . (1)、求点A的坐标.(2)、求抛物线的表达式.(3)、当以 、 、 、 为顶点的四边形是平行四边形时,求 的值.24. 定义:在三角形中,把一边的中点到这条边的高线的距离叫做这条边的中垂距.
(1)、求点A的坐标.(2)、求抛物线的表达式.(3)、当以 、 、 、 为顶点的四边形是平行四边形时,求 的值.24. 定义:在三角形中,把一边的中点到这条边的高线的距离叫做这条边的中垂距.例:如图①,在△ABC中,D为边BC的中点,AE⊥BC于E,则线段DE的长叫做边BC的中垂距.
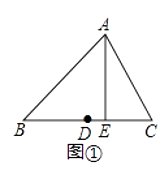 (1)、设三角形一边的中垂距为d(d≥0).若d=0,则这样的三角形一定是 , 推断的数学依据是 .(2)、如图②,在△ABC中,∠B=45°,AB= ,BC=8,AD为边BC的中线,求边BC的中垂距.
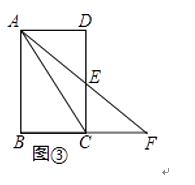
(1)、设三角形一边的中垂距为d(d≥0).若d=0,则这样的三角形一定是 , 推断的数学依据是 .(2)、如图②,在△ABC中,∠B=45°,AB= ,BC=8,AD为边BC的中线,求边BC的中垂距.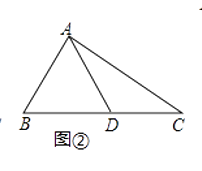 (3)、如图③,在矩形ABCD中,AB=6,AD=4.点E为边CD的中点,连结AE并延长交BC的延长线于点F,连结AC.求△ACF中边AF的中垂距.
(3)、如图③,在矩形ABCD中,AB=6,AD=4.点E为边CD的中点,连结AE并延长交BC的延长线于点F,连结AC.求△ACF中边AF的中垂距.