吉林省长春市朝阳区2018-2019学年九年级上学期数学期末考试试卷
试卷更新日期:2019-12-21 类型:期末考试
一、单选题
-
1. 若二次根式 有意义,则x的取值范围为( )A、x>2 B、x<2 C、x≤2 D、x≥22. “汽车行驶到有交通信号灯的路口时,前方恰好遇到绿灯”,这个事件是( )A、确定事件 B、随机事件 C、不可能事件 D、必然事件3. 在平面直角坐标系中,将抛物线y=﹣2(x﹣1)2+3向下平移2个单位后所得抛物线的表达式为( )A、y=﹣2(x+1)2+3 B、y=﹣2(x﹣3)2+3 C、y=﹣2(x﹣1)2+5 D、y=﹣2(x﹣1)2+14. 中国古代在利用“计里画方”(比例缩放和直角坐标网格体系)的方法制作地图时,会利用测杆、水准仪和照板来测量距离.在如图所示的测量距离AB的示意图中,记照板“内芯”的高度为EF.观测者的眼睛(图中用点C表示)与BF在同一水平线上,则下列结论中,正确的是( )
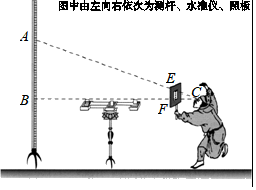 A、 B、 C、 D、5. 如图,在长为32m , 宽为20m的矩形空地上修建同样宽的道路(图中阴影部分),剩余的空地上种植草坪,使草坪的面积为540m2 . 设道路的宽为xm , 根据题意,下面列出的方程正确的是( )
A、 B、 C、 D、5. 如图,在长为32m , 宽为20m的矩形空地上修建同样宽的道路(图中阴影部分),剩余的空地上种植草坪,使草坪的面积为540m2 . 设道路的宽为xm , 根据题意,下面列出的方程正确的是( ) A、32x+20x﹣2x2=540 B、32x+20x=32×20﹣540 C、(32﹣x)(20﹣x)=540 D、(32﹣x)(20﹣x)=32×20﹣5406. 抛物线y=(x+1)2+1上有点A(x1 , y1)点B( x2 , y2)且x1<x2<﹣1,则y1与y2的大小关系是( )A、y1<y2 B、y1>y2 C、y1=y2 D、不能确定7. 在三角形纸片ABC中,AB=8,BC=4,AC=6,按下列方法沿虚线剪下,能使阴影部分的三角形与△ABC相似的是( )A、
A、32x+20x﹣2x2=540 B、32x+20x=32×20﹣540 C、(32﹣x)(20﹣x)=540 D、(32﹣x)(20﹣x)=32×20﹣5406. 抛物线y=(x+1)2+1上有点A(x1 , y1)点B( x2 , y2)且x1<x2<﹣1,则y1与y2的大小关系是( )A、y1<y2 B、y1>y2 C、y1=y2 D、不能确定7. 在三角形纸片ABC中,AB=8,BC=4,AC=6,按下列方法沿虚线剪下,能使阴影部分的三角形与△ABC相似的是( )A、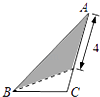 B、
B、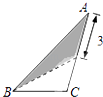 C、
C、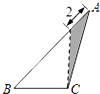 D、
D、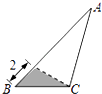
二、填空题
-
8. 计算:tan45°=.9. 若关于x的一元二次方程 有两个相等的实数根,则a的值是 .10. 已知二次函数y=ax2+bx+c(a≠0)的图象与x轴的两个交点的横坐标分别为 , ,则此二次函数图象的对称轴为.11. 如图,在平面直角坐标系中,△ABC和△A′B′C′是以坐标原点O为位似中心的位似图形,点B、B′的坐标分别为(3,1)、(6,2)若点A的坐标为( ,3),则点A′的坐标为 .
 12. 如图,在平面直角坐标系中,抛物线 的顶点为A , 与x轴分别交于O、B两点.过顶点A分别作AC⊥x轴于点C , AD⊥y轴于点D , 连结BD , 交AC于点E , 则△ADE与△BCE的面积和为 .
12. 如图,在平面直角坐标系中,抛物线 的顶点为A , 与x轴分别交于O、B两点.过顶点A分别作AC⊥x轴于点C , AD⊥y轴于点D , 连结BD , 交AC于点E , 则△ADE与△BCE的面积和为 . 13. 如图,在5×5的正方形网格中,每个小正方形的边长均为1,点A、B、C都在格点上,则cos∠BAC的值为 .
13. 如图,在5×5的正方形网格中,每个小正方形的边长均为1,点A、B、C都在格点上,则cos∠BAC的值为 .
三、解答题
-
14. 计算:15. 已知关于x的方程x2﹣(2k+1)x+k2+k=0的一个根是1,求k的值.16. 在一个不透明的盒子里装着三张卡片,分别标记为A、B、B , 每张卡片除图案不同外其余均相同,卡片上的图案分别为正方形和等边三角形.从盒子里随机抽出一张卡片,记下图案后放回并搅匀;再随机抽出一张卡片记下图案.用画树状图(或列表)的方法,求两次抽出的卡片上的图案都是等边三角形的概率.
 17. 在平面直角坐标系中,抛物线y=ax2+bx(a≠0)经过(﹣2,0)、(1,﹣6)两点.(1)、求a、b的值.(2)、求抛物线的顶点坐标.18. 如图,游客在点A处坐缆车出发,沿A﹣B﹣D的路线可至山顶D处.已知AB=BD=800米,∠α=75°,∠β=45°,求山高DE(结果精确到1米).
17. 在平面直角坐标系中,抛物线y=ax2+bx(a≠0)经过(﹣2,0)、(1,﹣6)两点.(1)、求a、b的值.(2)、求抛物线的顶点坐标.18. 如图,游客在点A处坐缆车出发,沿A﹣B﹣D的路线可至山顶D处.已知AB=BD=800米,∠α=75°,∠β=45°,求山高DE(结果精确到1米).(参考数据:sin75°=0.966,cos75°=0.259,tan75°=3.732,
 =1.414)
=1.414) 19. 如图,在Rt△ABC中,∠C=90°,BC=6,AC=8.AB的垂直平分线DE交AB于点D , 交AC于点E .
19. 如图,在Rt△ABC中,∠C=90°,BC=6,AC=8.AB的垂直平分线DE交AB于点D , 交AC于点E . (1)、求AD的长.(2)、求DE的长.20. 如图,是一座古拱桥的截面图,拱桥桥洞的上沿是抛物线形状,当水面的宽度为10m时,桥洞与水面的最大距离是5m .
(1)、求AD的长.(2)、求DE的长.20. 如图,是一座古拱桥的截面图,拱桥桥洞的上沿是抛物线形状,当水面的宽度为10m时,桥洞与水面的最大距离是5m .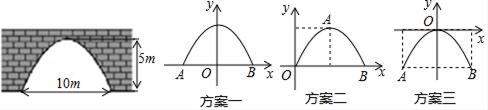 (1)、经过讨论,同学们得出三种建立平面直角坐标系的方案(如图),你选择的方案是(填方案一,方案二,或方案三),则B点坐标是 , 求出你所选方案中的抛物线的表达式;(2)、因为上游水库泄洪,水面宽度变为6m , 求水面上涨的高度.21. 在平面直角坐标系中,抛物线y1=x2﹣4x+3与直线y2=x+3分别交于A(0,3)B(5,8)两点.(1)、感知:当y1=y2时,结合图象可以得到方程x2﹣4x+3=x+3的解为x1=0,x2=5
(1)、经过讨论,同学们得出三种建立平面直角坐标系的方案(如图),你选择的方案是(填方案一,方案二,或方案三),则B点坐标是 , 求出你所选方案中的抛物线的表达式;(2)、因为上游水库泄洪,水面宽度变为6m , 求水面上涨的高度.21. 在平面直角坐标系中,抛物线y1=x2﹣4x+3与直线y2=x+3分别交于A(0,3)B(5,8)两点.(1)、感知:当y1=y2时,结合图象可以得到方程x2﹣4x+3=x+3的解为x1=0,x2=5探究:当y1>y2时,结合图象可以得到不等式x2﹣4x+3>x+3的解集为;
当y1<y2时,结合图象可以得到不等式x2﹣4x+3<x+3的解集为 .
(2)、应用:过点P(0,m)作直线l⊥y轴,将抛物线y1=x2﹣4x+3在直线l下方的图象沿直线l翻折后得到的图象记为图象G . 当图象G在直线y2=x+3上方的部分对应的x的取值范围为1<x<2时,直接写出m的值为 . 22. 如图,△ABC是等边三角形,AB=6.动点P从点A出发,沿AB以每秒2个单位长度的速度向终点B运动.过点P作PD⊥AC于点D,以PD为边向右作矩形PDEF,且PA=PF,点M为AC中点,连接PM.设矩形PDEF与△ABC重叠部分的面积为S,点P运动的时间为t(t>0)秒.
22. 如图,△ABC是等边三角形,AB=6.动点P从点A出发,沿AB以每秒2个单位长度的速度向终点B运动.过点P作PD⊥AC于点D,以PD为边向右作矩形PDEF,且PA=PF,点M为AC中点,连接PM.设矩形PDEF与△ABC重叠部分的面积为S,点P运动的时间为t(t>0)秒.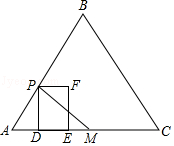 (1)、填空:PD=(用含t的代数式表示).(2)、当点F落在BC上时,求t的值.(3)、求S与t之间的函数关系式.(4)、直接写出直线PM将矩形PDEF分成两部分的面积比为1:3时t的值.23. 在平面直角坐标系中,抛物线y=ax2﹣2ax﹣1交y轴于点C .(1)、点C的坐标为 .(2)、当点P(3,5)在二次函数y=ax2﹣2ax﹣1的图象上时,求a的值.(3)、当a=1时,抛物线交x轴于A、B两点(点A在点B的左侧).点Q是抛物线上一点,且横坐标为m , 当S△ABC=S△ABQ , 求m的值.(4)、点M、N的坐标分别为( ,2)、( ,2),连结MN . 直接写出线段MN与二次函数y=ax2﹣2ax﹣1的图象只有1个交点时a的取值范围.
(1)、填空:PD=(用含t的代数式表示).(2)、当点F落在BC上时,求t的值.(3)、求S与t之间的函数关系式.(4)、直接写出直线PM将矩形PDEF分成两部分的面积比为1:3时t的值.23. 在平面直角坐标系中,抛物线y=ax2﹣2ax﹣1交y轴于点C .(1)、点C的坐标为 .(2)、当点P(3,5)在二次函数y=ax2﹣2ax﹣1的图象上时,求a的值.(3)、当a=1时,抛物线交x轴于A、B两点(点A在点B的左侧).点Q是抛物线上一点,且横坐标为m , 当S△ABC=S△ABQ , 求m的值.(4)、点M、N的坐标分别为( ,2)、( ,2),连结MN . 直接写出线段MN与二次函数y=ax2﹣2ax﹣1的图象只有1个交点时a的取值范围.