吉林长春市宽城区2018-2019学年八年级上学期数学期末考试试卷
试卷更新日期:2019-12-21 类型:期末考试
一、单选题
-
1. 若分式 在实数范围内有意义,则实数x的取值范围是( )A、x>﹣2 B、x<﹣2 C、x=﹣2 D、x≠﹣2
-
2. 下列运算正确的是( )A、 B、 C、 D、
-
3. 将多项式x﹣x3因式分解正确的是( )A、x(1﹣x2) B、x(x2﹣1) C、x(1+x)(1﹣x) D、x(x+1)(x﹣1)
-
4. 对于命题“在同一平面内,若a∥b,a∥c,则b∥c”,用反证法证明,应假设( )A、a⊥c B、b⊥c C、a与c相交 D、b与c相交
-
5. 如图,在△ABC中,边AC的垂直平分线交边AB于点D,连结CD.若∠A=50°,则∠BDC的大小为( )
 A、90° B、100° C、120° D、130°
A、90° B、100° C、120° D、130° -
6. 如图,点D,E分别在线段AB,AC上,CD与BE相交于O点,已知AB=AC,现添加以下的哪个条件仍不能判定△ABE≌△ACD( )
 A、∠B=∠C B、AD=AE C、BD=CE D、BE=CD
A、∠B=∠C B、AD=AE C、BD=CE D、BE=CD -
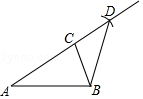
7. 如图, 、 分别是 的中线和角平分线.若 , ,则 的大小是( )
 A、 B、 C、 D、
A、 B、 C、 D、 -
8. “赵爽弦图”巧妙地利用面积关系证明了勾股定理,是我国古代数学的骄傲.如图所示的“赵爽弦图”是由四个全等的直角三角形和一个小正方形拼成的一个大正方形.设直角三角形较长直角边长为a,较短直角边长为b,若ab=8,大正方形的面积为25,则小正方形的边长为( )
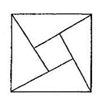 A、4 B、3 C、2 D、1
A、4 B、3 C、2 D、1
二、填空题
-
9. 计算:24a3b2÷3ab= .
-
10. 分式 的值为0,那么x的值为 .
-
11. 某班50名学生在2018年适应性考试中,数学成绩在100〜110分这个分数段的频率为0.2,则该班在这个分数段的学生为人.
-
12. 如图,在△ABC中,AB=AC.以点C为圆心,以CB长为半径作圆弧,交AC的延长线于点D,连结BD.若∠A=32°,则∠CDB的大小为度.
-
13. 如图,在 中, 平分 交 于点 , 于点 , 、 交于点 .若 , ,则 的面积是 .

-
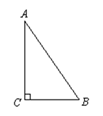
14. 《九章算术》是我国古代最重要的数学著作之一,在“勾股”章中记载了一道“折竹抵地”问题:“今有竹高一丈,末折抵地,去本三尺,问折者高几何?”翻译成数学问题是:如图,在△ABC中,∠ACB=90º,AC+AB=10,BC=3,则AC= .
三、解答题
-
15. 计算: .
-
16. 化简: • .
-
17. 图①、图②是 的正方形网格, 、 两点均在格点上.在图①、图②中各画一个顶点在格点、以 为一边的等腰三角形,且所画两个三角形不全等.
图①
 图②
图② 
-
18. 先化简,再求值: ,其中 .
-
19. 如图,在正方形网格中,每个小正方形的边长均为1,△ABC的三个顶点分别在正方形网格的格点上.
 (1)、计算边AB、BC、AC的长.(2)、判断△ABC的形状,并说明理由.
(1)、计算边AB、BC、AC的长.(2)、判断△ABC的形状,并说明理由. -
20. 某中学八年级抽取部分学生进行跳绳测试.并规定:每分钟跳90次以下的为不及格;每分钟跳90~99次的为及格;每分钟跳100~109次的为中等;每分钟跳110~119次的为良好;每分钟跳120次及以上的为优秀.测试结果整理绘制成如下两幅不完整的统计图.请根据图中信息,解答下列问题:
 (1)、参加这次跳绳测试的共有多少人?(2)、所以参加这次跳绳测试的共有50人.把条形统计图补充完整.(3)、求“中等”部分所在扇形对应的圆心角的度数.
(1)、参加这次跳绳测试的共有多少人?(2)、所以参加这次跳绳测试的共有50人.把条形统计图补充完整.(3)、求“中等”部分所在扇形对应的圆心角的度数. -
21. 如图,在 中, , 为 的中点, 于 , 于 ,且 .
 (1)、求证: .(2)、判断 的形状,并说明理由.
(1)、求证: .(2)、判断 的形状,并说明理由. -
22. 已知 、 、 分别是 的三边.(1)、分别将多项式 , 进行因式分解.(2)、若 ,试判断 的形状,并说明理由.
-
23. 问题原型:如图①,在锐角 中, ,AD⊥BC于D,在AD上取点E,使 ,连结BE.求证: .
问题原型:证明:∵ ,
∴ .
∴ .
∴ .
∴ .
∴ .
∵ ,
∴ .
∴
问题拓展:如图②,在问题原型的条件下, 为 的中点,连结 并延长至点 ,使 ,连结 .
图①
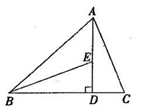 图②
图② 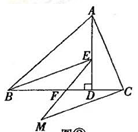 (1)、判断线段 与 的大小关系,并说明理由.(2)、若 ,直接写出 、 两点之间的距离.
(1)、判断线段 与 的大小关系,并说明理由.(2)、若 ,直接写出 、 两点之间的距离. -
24. 如图,在 中, , , , 平分 交 于 , 于点 .
 (1)、求证: 垂直平分 .(2)、求 的长(3)、求 的长.
(1)、求证: 垂直平分 .(2)、求 的长(3)、求 的长.
