吉林省长春市绿园区2018-2019学年八年级上学期数学期末考试试卷

试卷更新日期：2019-12-21 类型：期末考试

进入 出卷网 下载

一、单选题

  • 1.       16的算术平方根是（   ）

    A、±4 B、±2 C、4 D、﹣4

    查看试题解析

  • 2. 下列数中，比 3 大的实数是（   ）
    A、﹣5 B、0 C、3 D、2

    查看试题解析

  • 3. 化简 (-x)3·(-x)2 的结果正确的是 （     ）
    A、-x6 B、x6 C、x5 D、–x5

    查看试题解析

  • 4. 若 a 的值使 x2+4x+a＝(x+2)2 成立，则 a 的值为（ ）
    A、5 B、4 C、3 D、2

    查看试题解析

  • 5. 如图，AB与CD相交于点E ， EA＝EC ， DE＝BE ， 若使△AED≌△CEB ， 则（　　）

    A、应补充条件∠A＝∠C B、应补充条件∠B＝∠D C、不用补充条件 D、以上说法都不符合题意

    查看试题解析

  • 6. 下列命题中，为真命题的是（ ）
    A、对顶角相等 B、同位角相等 C、若 a2=b2 ，则 a=b D、若 a>b ，则 −2a>−2b

    查看试题解析

  • 7. 如图，在△ABC 中，AB＝AC，D 是 BC 的中点，∠B＝40°，则∠BAD＝（ ）

    A、100° B、80° C、50° D、40°

    查看试题解析

  • 8. 如图，在高为3米，斜坡长为5米的楼梯台阶上铺地毯，则地毯的长度至少要（   ）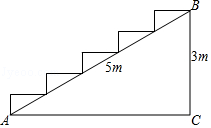

    A、4米 B、5米 C、6米 D、7米

    查看试题解析

二、填空题

  • 9. 因式分解：xy2﹣x2y= ．

    查看试题解析

  • 10. 计算（x﹣1）（2x+3）的结果是 ．

    查看试题解析

  • 11. 如图，是光明中学七年级（2）班四个小组交的创新教育实践的调查报告，四个小组中交的篇数最多的有篇，占全班总数的%．

    查看试题解析

  • 12. 如图，点B、D、C、F在同一条直线上，且BC=FD，AB=EF、请你只添加一个条件（不再加辅助线），使△ABC≌△EFD，你添加的条件是 ．

    查看试题解析

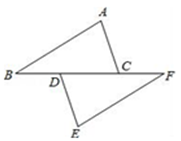  • 13. 如图，利用图形面积的不同表示方法，能够得到的代数恒等式是(写出一个即可)．

    查看试题解析

  • 14. 如图，矩形OABC的边OA长为2，边AB长为1，OA在数轴上，以原点O为圆心，对角线OB的长为半径画弧，交数轴上原点右边于一点，则这个点表示的实数是 ．

    查看试题解析

三、解答题

  • 15. 先化简再求值：（a+b）（a﹣b）+（a+b）2﹣2a2 ， 其中a＝﹣3，b＝ 13 ．

    查看试题解析

  • 16. 如图1，是一个长为2m，宽为2n的长方形，沿图中虚线用剪刀将其均分成四个完全相同的小长方形，然后按图2的形状拼图．

    (1)、图2中的图形阴影部分的边长为；(用含m、n的代数式表示)
    (2)、请你用两种不同的方法分别求图2中阴影部分的面积；

    方法一：；

    方法二： ．

    (3)、观察图2，请写出代数式(m+n)2、(m﹣n)2、4mn之间的关系式： ．

    查看试题解析

  • 17. 先阅读下面的例题，再解答后面的题目．

    例：已知x2+y2﹣2x+4y+5＝0，求x+y的值．

    解：由已知得（x2﹣2x+1）+（y2+4y+4）＝0，

    即（x﹣1）2+（y+2）2＝0．

    因为（x﹣1）2≥0，（y+2）2≥0，它们的和为0，

    所以必有（x﹣1）2＝0，（y+2）2＝0，

    所以x＝1，y＝﹣2．

    所以x+y＝﹣1．

    题目：已知x2+4y2﹣6x+4y+10＝0，求xy的值．

    查看试题解析

  • 18. 如图，在△ ABC  中，点 D ， E  分别在边 AC ， AB  上， BD  与 CE  交于点 O ，给出下列三个条件：① ∠EBO=∠DCO ；② BE=CD ；③ OB=OC ．

    (1)、上述三个条件中，由哪两个条件可以判定△ ABC  是等腰三角形?（用序号写出所有成立的情形）
    (2)、请选择（1）中的一种情形，写出证明过程．

    查看试题解析

  • 19. 某班在一次班会课上，就“遇见路人摔倒后如何处理”的主题进行讨论，并对全班 50 名学生的处理方式进行统计，得出相关统计表和统计图．

    组别

    A

    B

    C

    D

    处理方式

    迅速离开

    马上救助

    视情况而定

    只看热闹

    人数

    m

    30

    n

    5

    请根据表图所提供的信息回答下列问题：

    (1)、求统计表中的m、n的值；
    (2)、补全频数分布直方图；
    (3)、若该校有 2000 名学生，请据此估计该校学生采取“马上救助”方式的学生有多少人？

    查看试题解析

  • 20. 如图，在正方形网格中，每个小正方形的边长均为 1，△ABC  的三个顶点都在格点上.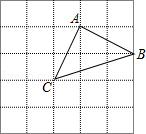

    (1)、直接写出边 AB、AC、BC 的长．
    (2)、判断△ABC 的形状，并说明理由．

    查看试题解析

  • 21. 如图，在等边三角形ABC中，点D，E分别在边BC，AC上，且DE∥AB，过点E作EF⊥DE，交BC的延长线于点F.

    (1)、求∠F的度数；
    (2)、若CD=2，求DF的长.

    查看试题解析

  • 22. 探究和应用：

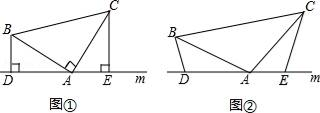    (1)、探究：如图①，在△ABC中，∠BAC＝90°，AB＝AC ， 直线m经过点A ， BD⊥m于点D ， CE⊥m于点E ， 求证：△ABD≌△CAE ．
    (2)、应用：如图②，在△ABC中，AB＝AC ， D、A、E三点都在直线m上，并且有∠BDA＝∠AEC＝∠BAC ， 求证：DE＝BD+CE ．

    查看试题解析

  • 23.                     
    (1)、你能求出（a﹣1）（a99+a98+a97+…+a2+a+1）的值吗？遇到这样的问题，我们可以先从简单的情况入手，分别计算下列各式的值．

    （a﹣1）（a+1）＝；

    （a﹣1）（a2+a+1）＝；

    （a﹣1）（a3+a2+a+1）＝；…

    由此我们可以得到：（a﹣1）（a99+a98+…+a+1）＝ ．

    (2)、利用（1）的结论，完成下面的计算：

    2199+2198+2197+…+22+2+1= ．

    查看试题解析

  • 24. 如图，在 Rt△ABC 中，∠C＝90°，AC＝8cm，BC＝6cm，M 在 AC上，且AM＝6cm，过点 A(与 BC 在 AC 同侧)作射线 AN⊥AC，若动点 P 从点 A 出发，沿射线 AN 匀速运动，运动速度为 1cm/s，设点 P 运动时间为 t 秒．

    (1)、经过几秒时，Rt△AMP 是等腰直角三角形？
    (2)、经过几秒时，PM⊥MB？
    (3)、经过几秒时，PM⊥AB？
    (4)、当△BMP 是等腰三角形时，直接写出 t 的所有值．

    查看试题解析