吉林省延边州2018-2019学年八年级上学期数学期末考试试卷
试卷更新日期：2019-12-21 类型：期末考试
一、单选题
-
1. 下列长度的三条线段能组成三角形的是（ ）A、3，4，8 B、5，6，11 C、1，2，3 D、5，6，102. 如果分式 的值为0，则x的值是A、1 B、0 C、－1 D、±13. 下列大学的校徽图案中，是轴对称图形的是（ ）A、
B、
C、
D、
4. 一个正多边形的每一个外角都等于45°，则这个多边形的边数为（ ）A、4 B、6 C、8 D、105. 将一副直角三角板按如图所示方式放置，使含30°角的三角板的一条直角边和含45°角的三角板的一条直角边重合，则∠1的度数为（ ）
A、45° B、65° C、70° D、75°6. 如图，在等边△ABC中，D是AB的中点，DE⊥AC于E ， EF⊥BC于F ， 已知AB＝8，则BF的长为（ ）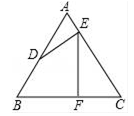
A、3 B、4 C、5 D、6二、填空题
-
7. 计算： ＝ ．8. 随着人们对环境的重视，新能源的开发迫在眉睫，石墨烯使现在世界上最薄的纳米材料，其理论厚度应是0.00000000034m，用科学记数法表示是 ．
9. 因式分解：x2﹣2xy+y2＝ ．10. 若分式 有意义，则x的取值范围为 ．11. 工人师傅在安装木制门框时，为防止变形常常像图中所示，钉上两条斜拉的木条，这样做的原理是根据三角形的性．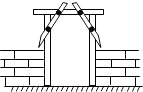
12. 如图，已知BD＝AC ， 那么添加一个条件后，能得到△ABC≌△BAD（只填一个即可）．
13.如图，将周长为8的△ABC沿BC方向向右平移1个单位得到△DEF，则四边形ABFD的周长为 ．
14. 如图，在三角形纸片ABC中，∠C＝90°，∠B＝30°，点D(不与B，C重合)是BC上任意一点，将此三角形纸片按如图的方式折叠，若EF的长度为a，则△DEF的周长为(用含a的式子表示)．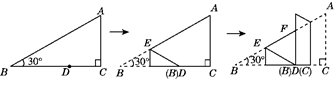
三、解答题
-
15. 先化简，再求值：（x+y）（x﹣y）+2y2 ， 其中x＝ ，y＝1．16. 解分式方程： ．17. 图1，图2，图3是在4×4的网格中有七个小正方形被涂黑，请你用三种不同的方法，在图1，图2，图3中分别涂黑三个小正方形，使整个图形成为轴对称图形（涂黑后的三个阴影部分图形不全等）
18. 如图，在△ABC中，∠C＝90°，∠B＝40°．
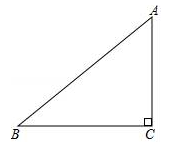(1)、请你用尺规作图，作AD平分∠BAC ， 交BC于点D（要求：保留作图痕迹）；(2)、∠ADC的度数．19. 如图，点C，E，F，B在同一直线上，点A，D在BC异侧，AB∥CD，AE=DF，∠A=∠D.
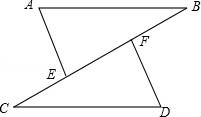(1)、求证：AB=CD；(2)、若AB=CF，∠B=30°，求∠D的度数.20.(1)、如图1，若大正方形的边长为a ， 小正方形的边长为b ， 则阴影部分的面积是；若将图1中的阴影部分裁剪下来，重新拼成如图2的一个矩形，则它长为；宽为；面积为 ．
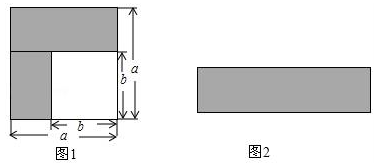(2)、由（1）可以得到一个公式： ．(3)、利用你得到的公式计算：20182﹣2019×2017．21. 八年级学生去距学校10千米的博物馆参观，一部分同学骑自行车先走，过了20分后，其余同学乘汽车出发，结果他们同时到达，已知汽车的速度是骑车同学速度的2倍，求骑车同学的速度．22. 如图，边长为a ， b的矩形，它的周长为14，面积为10，求下列各式的值：
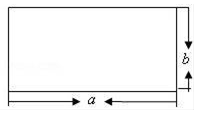(1)、a2b+ab2；(2)、a2+b2+ab ．23. 如图，△ABC三个顶点的坐标分别为A（1，1），B（4，2），C（3，4）．
(1)、作出与△ABC关于y轴对称△A1B1C1 ， 并写出三个顶点的坐标为：A1（），B1（），C1（）；(2)、在x轴上找一点P ， 使PA+PB的值最小，请直接写出点P的坐标．24. 某超市用3000元购进某种干果销售，由于销售状况良好，超市又调拨9000元资金购进该种干果，但这次的进价比第一次的进价提高了20%，购进干果数量是第一次的2倍还多300千克，如果超市按每千克9元的价格出售，当大部分干果售出后，余下的600千克按售价的8折售完．(1)、该种干果的第一次进价是每千克多少元？(2)、超市销售这种干果共盈利多少元？25. 如图，△ABC是等边三角形，点D在AC上，点E在BC的延长线上，且BD＝DE ．
(1)、若点D是AC的中点，如图1．求证：AD＝CE ．(2)、若点D不是AC的中点，如图2，试判断AD与CE的数量关系，并证明你的结论：（提示：过点D作DF∥BC ， 交AB于点F ． ）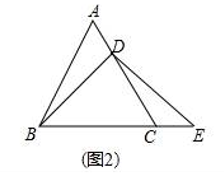
(3)、若点D在线段AC的延长线上，（2）中的结论是否仍成立？如果成立，给予证明；如果不成立，请说明理由．