吉林省四平市伊通县2018-2019学年八年级上学期数学期末考试试卷
试卷更新日期:2019-12-21 类型:期末考试
一、单选题
-
1. 有两根木棒长分别为10cm和18cm,要钉成一个三角形木架,则下列四根木棒应选取( )A、8cm B、12cm C、30cm D、40cm2. 下列三角形中,不是轴对称图形的是( )A、有两个角相等的三角形 B、有两个角分别是120°和30°的三角形 C、有一个角是45°的直角三角形 D、有一个角是60°的直角三角形3. 下列运算中,结果是a6的是( )A、a2•a3 B、a12÷a2 C、(a3)3 D、(﹣a)64. 如图,在△ABC中,AB=AC=20cm,DE垂直平分AB,垂足为E,交AC于D,若△DBC的周长为35cm,则BC的长为( )
 A、5cm B、10cm C、15cm D、17.5cm5. 已知a+b=m,ab=n,则(a﹣b)2等于( )A、m2﹣n B、m2+n C、m2+4n D、m2﹣4n6. 小军家距学校5千米,原来他骑自行车上学,学校为保障学生安全,新购进校车接送学生,若校车速度是他骑车速度的2倍,现在小军乘校车上学可以从家晚10分钟出发,结果与原来到校时间相同.设小军骑车的速度为x千米/小时,则所列方程正确的为( )A、 + = B、 ﹣ = C、 +10= D、 ﹣10=
A、5cm B、10cm C、15cm D、17.5cm5. 已知a+b=m,ab=n,则(a﹣b)2等于( )A、m2﹣n B、m2+n C、m2+4n D、m2﹣4n6. 小军家距学校5千米,原来他骑自行车上学,学校为保障学生安全,新购进校车接送学生,若校车速度是他骑车速度的2倍,现在小军乘校车上学可以从家晚10分钟出发,结果与原来到校时间相同.设小军骑车的速度为x千米/小时,则所列方程正确的为( )A、 + = B、 ﹣ = C、 +10= D、 ﹣10=二、填空题
-
7. 若n边形内角和为900°,则边数n= .
8. 分解因式:2x2-8y2=.9. 已知:x2+16x﹣k是完全平方式,则k= .10. 若分式 的值为0,则x= .11. 如图,在Rt△ABC中,∠C=90°,AD平分∠BAC,交BC于点D,若AB=10,CD=3,则S△ABD= . 12. 如图,分别以线段BC的两个端点为圆心,以大于 BC长为半径画弧,两弧分别相交于D、E两点,直线DE交BC于点F,点A是直线DE上的一点,连接AB、AC,若AB=12cm,∠C=60°,则CF=cm.
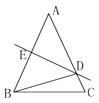
12. 如图,分别以线段BC的两个端点为圆心,以大于 BC长为半径画弧,两弧分别相交于D、E两点,直线DE交BC于点F,点A是直线DE上的一点,连接AB、AC,若AB=12cm,∠C=60°,则CF=cm. 13. 如图,△ABC是等边三角形,D,E分别是AC,BC上的两点,且AD=CE,AE,BD相交于点N,则∠DNE的度数是 .
13. 如图,△ABC是等边三角形,D,E分别是AC,BC上的两点,且AD=CE,AE,BD相交于点N,则∠DNE的度数是 . 14. 如图,在△ABC中,AB=AC=4,∠A=30°,那么S△ABC= .
14. 如图,在△ABC中,AB=AC=4,∠A=30°,那么S△ABC= . 15. 分解因式:x2y+2xy2+y3 .
15. 分解因式:x2y+2xy2+y3 .三、解答题
-
16. 解分式方程: =1.17. 计算:x2(x﹣1)﹣x(x2+x﹣1)18. 已知:如图A、F、B、D四点在同一直线上,且AC=DE,CB=EF,AF=DB.
求证:∠A=∠D.
 19. 先化简,再求值: ÷( +a+2),其中a满足等式|a+1|=0.20. 图①、图②都是4×4的正方形网格,每个小正方形的顶点称为格点,每个小正方形的边长均为1.在每个网格中标注了5个格点,按下列要求画图:
19. 先化简,再求值: ÷( +a+2),其中a满足等式|a+1|=0.20. 图①、图②都是4×4的正方形网格,每个小正方形的顶点称为格点,每个小正方形的边长均为1.在每个网格中标注了5个格点,按下列要求画图: (1)、在图①中,以格点为顶点画一个等腰三角形,使其内部已标注的格点只有3个;(2)、在图②中,以格点为顶点画一个等腰三角形,使其内部已标注的格点只有2个,并且面积为3.21. 甲、乙两人共同计算一道整式乘法题:(2x+a)(3x+b).甲由于把第一个多项式中的“+a”看成了“﹣a”,得到的结果为6x2+11x﹣10;乙由于漏抄了第二个多项式中x的系数,得到的结果为2x2﹣9x+10.(1)、求正确的a、b的值.(2)、计算这道乘法题的符合题意结果.22. 如图,“中国海监50”于上午11时30分在南海海域A处巡逻,观测到岛礁B在北偏东60°,该船以每小时10海里的速度向正东航行到C处,观测岛礁B在北偏东30°,继续向正东航行到D处时,再观测到岛礁B在北偏西30°,当海监船到达C处时恰与岛礁B相距20海里,请你分别确定“中国海监50”从A处到达C处和D处所用的时间.
(1)、在图①中,以格点为顶点画一个等腰三角形,使其内部已标注的格点只有3个;(2)、在图②中,以格点为顶点画一个等腰三角形,使其内部已标注的格点只有2个,并且面积为3.21. 甲、乙两人共同计算一道整式乘法题:(2x+a)(3x+b).甲由于把第一个多项式中的“+a”看成了“﹣a”,得到的结果为6x2+11x﹣10;乙由于漏抄了第二个多项式中x的系数,得到的结果为2x2﹣9x+10.(1)、求正确的a、b的值.(2)、计算这道乘法题的符合题意结果.22. 如图,“中国海监50”于上午11时30分在南海海域A处巡逻,观测到岛礁B在北偏东60°,该船以每小时10海里的速度向正东航行到C处,观测岛礁B在北偏东30°,继续向正东航行到D处时,再观测到岛礁B在北偏西30°,当海监船到达C处时恰与岛礁B相距20海里,请你分别确定“中国海监50”从A处到达C处和D处所用的时间. 23. 某县为了落实中央的“强基惠民工程”,计划将某村的居民自来水管道进行改造.该工程若由甲队单独施工恰好在规定时间内完成;若乙队单独施工,则完成工程所需天数是规定天数的1.5倍.如果由甲、乙队先合做15天,那么余下的工程由甲队单独完成还需5天.(1)、这项工程的规定时间是多少天?(2)、已知甲队每天的施工费用为6500元,乙队每天的施工费用为3500元.为了缩短工期以减少对居民用水的影响,工程指挥部最终决定该工程由甲、乙队合做来完成.则该工程施工费用是多少?24.(1)、问题发现
23. 某县为了落实中央的“强基惠民工程”,计划将某村的居民自来水管道进行改造.该工程若由甲队单独施工恰好在规定时间内完成;若乙队单独施工,则完成工程所需天数是规定天数的1.5倍.如果由甲、乙队先合做15天,那么余下的工程由甲队单独完成还需5天.(1)、这项工程的规定时间是多少天?(2)、已知甲队每天的施工费用为6500元,乙队每天的施工费用为3500元.为了缩短工期以减少对居民用水的影响,工程指挥部最终决定该工程由甲、乙队合做来完成.则该工程施工费用是多少?24.(1)、问题发现如图1,

△ACB和△DCE均为等边三角形,点A,D,E在同一直线上,连接BE.
填空:①求∠AEB的度数;②求线段AD,BE之间的数量关系为.
(2)、拓展探究如图2,△ACB和△DCE均为等腰直角三角形,∠ACB=∠DCE=90°,点A,D,E在同一直线上,CM为△DCE中DE边上的高,连接BE,请判断∠AEB的度数及线段CM,AE,BE之间的数量关系,并说明理由.
