吉林省长春市朝阳区2018-2019学年七年级上学期数学期末考试试卷

试卷更新日期：2019-12-21 类型：期末考试

进入出卷网下载

一、单选题

1. 2019的相反数是（）

A、2019 B、-2019 C、 $\frac{1}{2019}$ D、 $- \frac{1}{2019}$

查看试题解析
2. 下图是由四个大小相同的正方体搭成的几何体，则它的主视图是（）

A、 B、 C、 D、

查看试题解析
3. 若一个整数12500…0用科学记数法表示为1.25×10¹⁰ ，则原数中“0”的个数为（　　）

A、5 B、8 C、9 D、10

查看试题解析
4. 计算 $3 a^{3} - a^{3}$ 的结果是 $($ 　　 $)$

A、2 B、 $2 a$ C、 $2 a^{3}$ D、 $3 a^{3}$

查看试题解析
5. 中国人最先使用负数，魏晋时期的数学家刘徽在“正负术”的注文中指出，可将算筹（小棍形状的记数工具）正放表示正数，斜放表示负数．如图①表示的是 $(+ 2) + (- 2)$ ，根据刘徵的这种表示法，可推算图②中所表示的算式为 $($ 　　 $)$

A、 $(+ 3) + (+ 6)$ B、 $(- 3) + (- 6)$ C、 $(- 3) + (+ 6)$ D、 $(+ 3) + (- 6)$

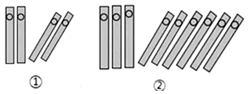查看试题解析
6. 如图，经过刨平的木板上的A，B两个点，能弹出一条笔直的墨线，而且只能弹出一条墨线，能解释这一实际应用的数学知识是（）

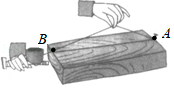A、两点之间，线段最短 B、两点确定一条直线 C、垂线段最短 D、在同一平面内，过一点有且只有一条直线与已知直线垂直

查看试题解析
7. 如图，直尺的一条边经过一个含45角的直角顶点直尺的一组对边分别与直角三角尺的两边相交，若∠1＝30°，则∠2的度数是(　　)

A、30° B、45° C、60° D、75°

查看试题解析
8. 如图，A是直线l外一点，过点A作AB⊥l于点B ，在直线l上取一点C ，连结AC ，使AC＝2AB ， P在线段BC上连结AP ．若AB＝3，则线段AP的长不可能是（　　）

A、3.5 B、4 C、5.5 D、6.5

查看试题解析

二、填空题

9. 比较大小：﹣11﹣12（填“＜”、或“＞”）．

查看试题解析
10. 如图，直线a、b被直线c所截，a∥b ，若∠1＝80°，则∠2的大小为度．

查看试题解析
11. 如图，射线 $O A$ 表示西北方向，若射线 $O B$ 表示南偏西 $60 °$ 的方向，则锐角 $∠ A O B$ 的大小是度．

查看试题解析
12. 如图将一直角三角板的直角顶点放置在两边互相平行的纸条的边上，若∠1＝35°，则∠2的大小为度．

查看试题解析
13. 用形状大小完全相同的等边三角形和正方形按如图所示的规律拼图案，即从第2个图案开始每个图案比前一个图案多4个等边三角形和1个正方形，则第n个图案中等边三角形的个数为个．

查看试题解析

三、解答题

14. 计算： $- 2 \frac{1}{2} + \frac{1}{2} - 1 =$ ．

查看试题解析
15. 计算： $6 \times \frac{1}{2} - {(- 1)}^{2} + {(- 2)}^{2} + 2$

查看试题解析
16. 先化简，再求值： $(2 a^{2} - 1 + a) - 2 (a - 1 + a^{2})$ ，其中 $a = - 12$ ．

查看试题解析
17. 如图①，长方体的上下底面是边长为 1 的正方形，高为2；如图②，在 $5 \times 5$ 的正方形网格中，每个小方格都是边长为1的正方形．

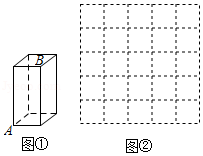(1)、在图②中画出这个长方体的一个展开图；

(2)、如果一只蚂蚁从顶点 $A$ 处沿长方体表面爬行到顶点 $B$ 处，请你在（1）中所画的展开图中画出该蚂蚁爬行的最短路线，并说明理由．

查看试题解析
18. 某面粉加工厂加工的面粉，用每袋可装10kg面粉的袋子装了200袋经过称重，质量超过标准质量10kg的用正数表示，质量低于标准质量10kg的用负数表示，结果记录如下
与标准质量的偏差(kg)
﹣1.5
﹣1
﹣0.5
0
0.5
1
2
袋数(袋)
40
30
10
25
40
20
35

(1)、求这批面粉的总质量；

(2)、如果100kg小麦加工80kg面粉，那么这批面粉是由多少千克小麦加工的？

查看试题解析
19. 如图，点A、B、C依次在同一条直线上，AB＝4，BC＝2，D是AB的中点，E是BC的中点．

(1)、AE的长为；

(2)、求DE的长．

查看试题解析
20. 如图，在四边形ABCD中，E、F分别是CD、AB延长线上的点，连结EF，分别交AD、BC于点G、H．若∠1＝∠2，∠A＝∠C，试说明AD∥BC和AB∥CD．

请完成下面的推理过程，并填空（理由或数学式）：

∵∠1＝∠2（）

∠1＝∠AGH（）

∴∠2＝∠AGH（）

∴AD∥BC（）

∴∠ADE＝∠C（）

∵∠A＝∠C（）

∴∠ADE＝∠A

∴AB∥CD（）

查看试题解析
21. （规定） $| \begin{array}{l} a & b \\ c & d \end{array} | = a - b + c - d$ ．
（理解）例如： $| \begin{array}{l} 3 & 2 \\ 1 & - 3 \end{array} | = 3 - 2 + 1 - (- 3) = 5$ ．

（应用）先化简，再求值： $| \begin{array}{l} 3 x y + 2 x^{2} & 2 x y + y^{2} \\ - x^{2} + 2 & 2 - x y \end{array} |$ ，其中 $x = - 2$ ， $y = - \frac{1}{2}$ ．

查看试题解析
22. 如图，直线AB、CD相交于点O，过点O作OE⊥AB，OF平分∠BOD．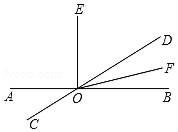

(1)、直接写出∠AOC的补角；

(2)、若∠AOC＝40°，求∠EOF的度数．

查看试题解析
23. 为提倡全民健身活动，某社区准备购买羽毛球和羽毛球拍供社区居民使用，某体育用品商店羽毛球每盒10元，羽毛球拍每副40元．该商店有两种优惠方案，方案一：不购买会员卡时，羽毛球享受8.5折优惠，羽毛球拍购买5副（含5副）以上才能享受8.5折优惠，5副以下必须按定价购买；方案二：每张会员卡20元，办理会员卡时，全部商品享受8折优惠．设该社区准备购买羽毛球拍6副，羽毛球 $a$ 盒，请回答下列问题：

(1)、如果一位体育爱好者按方案一只购买了4副羽毛球拍，求他购买时所需要的费用；

(2)、用含 $a$ 的代数式分别表示该社区按方案一和方案二购买所需要的钱数；

(3)、①直接写出一个 $a$ 的值，使方案一比方案二优惠；
②直接写出一个 $a$ 的值，使方案二比方案一优惠．

查看试题解析
24.

(1)、（感知）如图①，AB∥CD，点E在直线AB与CD之间，连结AE、BE，试说明∠BEE+∠DCE＝∠AEC．下面给出了这道题的解题过程，请完成下面的解题过程，并填空（理由或数学式）：
解：如图①，过点E作EF∥AB
∴∠BAE＝∠1（　　）
∵AB∥CD（　　）
∴CD∥EF（　　）
∴∠2＝∠DCE
∴∠BAE+∠DCE＝∠1+∠2（　　）
∴∠BAE+∠DCE＝∠AEC

(2)、（探究）当点E在如图②的位置时，其他条件不变，试说明∠AEC+∠FGC+∠DCE＝360°；

(3)、（应用）点E、F、G在直线AB与CD之间，连结AE、EF、FG和CG，其他条件不变，如图③．

若∠EFG＝36°，则∠BAE+∠AEF+∠FGC+∠DCG＝°．

查看试题解析

与标准质量的偏差(kg)	﹣1.5	﹣1	﹣0.5	0	0.5	1	2
袋数(袋)	40	30	10	25	40	20	35