吉林省吉林市2018-2019学年七年级上学期数学期末考试试卷
试卷更新日期:2019-12-21 类型:期末考试
一、单选题
-
1. 如果零上2℃记作+2℃,那么零下3℃记作()A、-3℃ B、-2℃ C、+3℃ D、+2℃2. 港珠澳大桥全长约为55000米,将数据55000科学记数法表示为( )A、0.55×105 B、5.5×104 C、55×103 D、550×1023. 如图所示的几何体从上面看得到的图形是( )
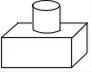 A、
A、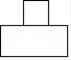 B、
B、 C、
C、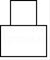 D、
D、 4. 若x﹣3=2y , 则x﹣2y的值是( )A、2 B、﹣2 C、3 D、﹣35. 下列计算中,正确的是( )A、x+x2=x3 B、2x2﹣x2=1 C、x2y﹣xy2=0 D、x2﹣2x2=﹣x26. 商店对某种手机的售价作了调整,按原售价的 8 折出售,此时的利润率为 14%,若此种手机的进价为 1200 元,设该手机的原售价为 x 元,则下列方程正确的是( )A、0.8x﹣1200=1200×14% B、0.8x﹣1200=14%x C、x﹣0.8x=1200×14% D、0.8x﹣1200=14%×0.8x
4. 若x﹣3=2y , 则x﹣2y的值是( )A、2 B、﹣2 C、3 D、﹣35. 下列计算中,正确的是( )A、x+x2=x3 B、2x2﹣x2=1 C、x2y﹣xy2=0 D、x2﹣2x2=﹣x26. 商店对某种手机的售价作了调整,按原售价的 8 折出售,此时的利润率为 14%,若此种手机的进价为 1200 元,设该手机的原售价为 x 元,则下列方程正确的是( )A、0.8x﹣1200=1200×14% B、0.8x﹣1200=14%x C、x﹣0.8x=1200×14% D、0.8x﹣1200=14%×0.8x二、填空题
-
7. 0的相反数是 .8. 已知|a+1|+(b﹣3)2=0,则 = .9. 种树时,只要定出两个树坑的位置,就能使同一行树坑在同一条直线上,其中的数学道理是 .10. 若﹣4xay+x2yb=﹣3x2y,则a+b= .11. 如图,图中阴影部分的面积是 .
 12. 将一副三角尺的直角顶点重合并按如图所示摆放,当AD平分∠BAC时,∠CAE= .
12. 将一副三角尺的直角顶点重合并按如图所示摆放,当AD平分∠BAC时,∠CAE= . 13. 若当x=﹣2018时,式子ax3﹣bx﹣3的值为5,则当x=2018时,式子ax3﹣bx﹣3的值为 .14. 已知点A在O的北偏西60°方向,点B在点O的南偏东40°方向,则∠AOB的度数为15. 如图,点C在线段AB上,点E、F分别是AB、AC的中点,若BC=4,则EF= .
13. 若当x=﹣2018时,式子ax3﹣bx﹣3的值为5,则当x=2018时,式子ax3﹣bx﹣3的值为 .14. 已知点A在O的北偏西60°方向,点B在点O的南偏东40°方向,则∠AOB的度数为15. 如图,点C在线段AB上,点E、F分别是AB、AC的中点,若BC=4,则EF= . 16. 某糕点厂中秋节前要制作一批盒装月饼,每盒中2块大月饼和4块小月饼,制作1块大月饼要用0.05kg面粉,制作1块小月饼要用0.02kg面粉,若现共有面粉540kg , 设可以生产x盒盒装月饼,则可列方程为 .
16. 某糕点厂中秋节前要制作一批盒装月饼,每盒中2块大月饼和4块小月饼,制作1块大月饼要用0.05kg面粉,制作1块小月饼要用0.02kg面粉,若现共有面粉540kg , 设可以生产x盒盒装月饼,则可列方程为 .三、解答题
-
17. 计算:12﹣(﹣18)+(﹣7)﹣15.18. 计算: .19. 计算(﹣10)3+[(﹣4)2﹣(1﹣32)×2].20. 解下列方程:8x﹣3(3x+2)=6.21.22. 先化简,再求值:5(3a2b﹣ab2)﹣(ab2+3a2b),其中a= ,b=﹣ .23. 在某年全军足球甲级A组的前11场比赛中,某队保持连续不败,共积23分.按比赛规则,胜一场得3分,平一场得1分,那么该队共胜了多少场?24. 新定义:若∠α的度数是∠β的度数的n倍,则∠α叫做∠β的n倍角.(1)、若∠M=10°21′,请直接写出∠M的3倍角的度数;(2)、如图1,

若∠AOB=∠BOC=∠COD , 请直接写出图中∠AOB的所有2倍角;
(3)、如图2,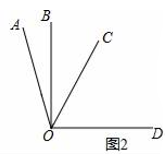
若∠AOC是∠AOB的3倍角,∠COD是∠AOB的4倍角,且∠BOD=90°,求∠BOC的度数.
25. 某玩具厂要生产500个芭比娃娃,此生产任务由甲、乙、丙三台机器承担,甲机器每小时生产12个,乙、丙两台机器的每小时生产个数之比为4:5.若甲、乙、丙三台机器同时生产,刚好在10小时25分钟完成任务.(1)、求乙、丙两台机器每小时各生产多少个?(2)、由于某种原因,三台机器只能按一定次序循环交替生产,且每台机器在每个循环中只能生产1小时,即每个循环需要3小时.①若生产次序为甲、乙、丙,则最后一个芭比娃娃由( )机器生产完成,整个生产过程共需( )小时;
②若想使完成生产任务的时间最少,直接写出三台机器的生产次序及完成生产任务的最少时间.
26. 点A、B在数轴上表示的数如图所示,动点P从点A出发,沿数轴向右以每秒1个单位长度的速度向点B运动到点B停止运动;同时,动点Q从点B出发,沿数轴向左以每秒2个单位长度的速度向点A运动,到点A停止运动设点P运动的时间为t秒,P、Q两点的距离为d(d≥0)个单位长度. (1)、当t=1时,d=;(2)、当P、Q两点中有一个点恰好运动到线段AB的中点时,求d的值;(3)、当点P运动到线段AB的3等分点时,直接写出d的值;(4)、当d=5时,直接写出t的值.
(1)、当t=1时,d=;(2)、当P、Q两点中有一个点恰好运动到线段AB的中点时,求d的值;(3)、当点P运动到线段AB的3等分点时,直接写出d的值;(4)、当d=5时,直接写出t的值.