2017年湖南省衡阳市高考数学三模试卷（理科）

试卷更新日期：2017-07-27 类型：高考模拟

进入出卷网下载

一、选择题

1. i是虚数单位，复数 $\frac{2}{1 - i} = a + b i (a ， b \in R)$ ，则a+b=（）

A、0 B、2 C、1 D、﹣2

查看试题解析
2. 设集合 $A = {(x ， y) | \frac{x^{2}}{4} + \frac{y^{2}}{16} = 1}$ ，B={（x，y）|y=3^x}，则A∩B的子集的个数是（）

A、4 B、3 C、2 D、1

查看试题解析
3. 已知sin（α+ $\frac{π}{3}$ ）+sinα=﹣ $\frac{4 \sqrt{3}}{5}$ ，﹣ $\frac{π}{2}$ ＜α＜0，则cos（α+ $\frac{2 π}{3}$ ）等于（）

A、﹣ $\frac{4}{5}$ B、﹣ $\frac{3}{5}$ C、 $\frac{4}{5}$ D、 $\frac{3}{5}$

查看试题解析
4. 为防止部分学生考试时用搜题软件作弊，命题组指派5名教师对数学卷的选择题、填空题和解答题这3种题型进行改编，则每种题型至少指派一名教师的不同分派方法种数为（）

A、150 B、180 C、200 D、280

查看试题解析
5. 执行如图所示的程序框图，若输出的S值为﹣4，则条件框内应填写（）

A、i＞3？ B、i＜5？ C、i＞4？ D、i＜4？

查看试题解析
6. 直三棱柱ABC﹣A₁B₁C₁中，底面是正三角形，三棱柱的高为 $\sqrt{3}$ ，若P是△A₁B₁C₁中心，且三棱柱的体积为 $\frac{9}{4}$ ，则PA与平面ABC所成的角大小是（）

A、 $\frac{π}{6}$ B、 $\frac{π}{4}$ C、 $\frac{π}{3}$ D、 $\frac{2 π}{3}$

查看试题解析
7. 函数f（x）=2sin（πx）﹣ $\frac{1}{1 - x}$ ，x∈[﹣2，4]的所有零点之和为（）

A、2 B、4 C、6 D、8

查看试题解析
8. 如图，网格纸上小正方形的边长为1，粗线画出的是某几何体的三视图，则该几何体最长的棱长为（）

A、 $4 \sqrt{3}$ B、 $4 \sqrt{2}$ C、6 D、 $2 \sqrt{5}$

查看试题解析
9. 已知对任意平面向量 $\vec{A B}$ =（x，y），把 $\vec{A B}$ 绕其起点沿逆时针旋转θ角得到向量 $\vec{A P}$ =（xcosθ﹣ysinθ，xsinθ+ycosθ），叫做把点B绕点A逆时针方向旋转角θ得到点P，设平面内曲线C上的每一点绕原点逆时针方向旋转 $\frac{π}{4}$ 后得到点的轨迹是曲线x²﹣y²=2，则原来曲线C的方程是（）

A、xy=﹣1 B、xy=1 C、y²﹣x²=2 D、y²﹣x²=1

查看试题解析
10. 已知F₁、F₂分别为双曲线C： $\frac{x^{2}}{4} - \frac{y^{2}}{5}$ =1的左、右焦点，P为双曲线C右支上一点，且|PF₁|=2|PF₂|，则△PF₁F₂外接圆的面积为（）

A、 $\frac{4 π}{15}$ B、 $\frac{16 π}{15}$ C、 $\frac{64 π}{15}$ D、 $\frac{256 π}{15}$

查看试题解析
11. 如图．在△ABC中，D是BC的中点，E、F是AD上的两个三等分点， $\vec{B A}$ • $\vec{C A}$ =4， $\vec{B F}$ • $\vec{C F}$ =﹣1，则 $\vec{B E}$ • $\vec{C E}$ 的值是（）

A、4 B、8 C、 $\frac{7}{8}$ D、 $\frac{3}{4}$

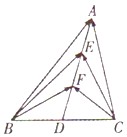查看试题解析
12. 《数学统综》有如下记载：“有凹线，取三数，小小大，存三角”．意思是说“在凹（或凸）函数（函数值为正）图象上取三个点，如果在这三点的纵坐标中两个较小数之和大于最大的数，则存在将这三点的纵坐标值作为三边长的三角形”．现已知凹函数f（x）=x²﹣2x+2，在 $[\frac{1}{3} ， m^{2} - m + 2]$ 上任取三个不同的点（a，f（a）），（b，f（b）），（c，f（c）），均存在以f（a），f（b），f（c）为三边长的三角形，则实数m的取值范围为（）

A、[0，1] B、 $[0 ， \frac{\sqrt{2}}{2})$ C、 $(0 ， \frac{\sqrt{2}}{2}]$ D、 $[\frac{\sqrt{2}}{2} ， \sqrt{2}]$

查看试题解析

二、填空题：

13. ${(x - \frac{2}{x^{2}})}^{6}$ 展开式中第三项为．

查看试题解析
14. 设函数f（x）= ${\begin{matrix} l n x ， x > 0 \\ - 2 x - 1 ， x \leq 0 \end{matrix}$ ，D是由x轴和曲线y=f（x）及该曲线在点（1，0）处的切线所围成的封闭区域，则z=x²+y²+2x+2y在D上的最小值为．

查看试题解析
15. 已知 $a_{n} = \int_{0}^{n} (2 x + 1) d x$ ，数列 ${\frac{1}{a_{n}}}$ 的前n项和为S_n ，数列{b_n}的通项公式为b_n=n﹣8，则b_nS_n的最小值为．

查看试题解析
16. 已知函数f（x）=log $_{\frac{1}{e}}$ （x²+ $\frac{1}{e}$ ）﹣| $\frac{x}{e}$ |，则使得f（x+1）＜f（2x﹣1）成立x的范围是．

查看试题解析

三、解答题

17. 已知数列{a_n}的首项a₁=4，当n≥2时，a_n_﹣1a_n﹣4a_n_﹣1+4=0，数列{b_n}满足b_n= $\frac{1}{2 - a_{n}} (n \in N^{*})$

(1)、求证：数列{b_n}是等差数列，并求{b_n}的通项公式；

(2)、若c_n=4^bn•（na_n﹣6），如果对任意n∈N^* ，都有c_n+ $\frac{1}{2}$ t≤2t² ，求实数t的取值范围．

查看试题解析
18. 据某市地产数据研究院的数据显示，2016年该市新建住宅销售均价走势如图所示，为抑制房价过快上涨，政府从8月份采取宏观调控措施，10月份开始房价得到很好的抑制．
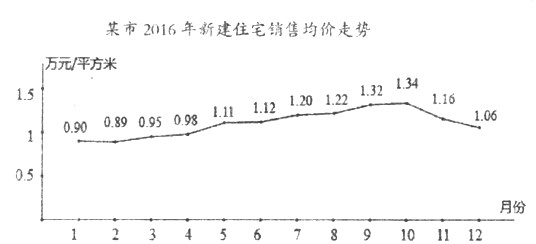
（Ⅰ）地产数据研究院研究发现，3月至7月的各月均价y（万元/平方米）与月份x之间具有较强的线性相关关系，试建立y关于x的回归方程（系数精确到0.01），政府若不调控，依次相关关系预测第12月份该市新建住宅销售均价；
（Ⅱ）地产数据研究院在2016年的12个月份中，随机抽取三个月份的数据作样本分析，若关注所抽三个月份的所属季度，记不同季度的个数为X，求X的分布列和数学期望．
参考数据： $\sum_{i = 1}^{5} x_{i}$ =25， $\sum_{i = 1}^{5} y_{i}$ =5.36， $\sum_{i = 1}^{5} (x_{i} - \bar{x}) (y_{i} - \bar{y})$ =0.64
回归方程 $\hat{y}$ = $\hat{b}$ x+ $\hat{a}$ 中斜率和截距的最小二乘估计公式分别为：
$\hat{b}$ = $\frac{\sum_{i = 1}^{n} (x_{i} - \bar{x}) (y_{i} - \bar{y})}{\sum_{i = 1}^{n} {(x_{i} - \bar{x})}^{2}}$ ， $\hat{a}$ = $\bar{y}$ ﹣ $\hat{b} \bar{x}$ ．

查看试题解析
19. 如图，在四棱柱ABCD﹣A₁B₁C₁D₁中，底面ABCD和侧面BCC₁B₁都是矩形，E是CD的中点，D₁E⊥CD，AB=2BC=2．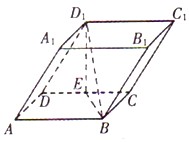

(1)、求证：BC⊥D₁E；

(2)、若平面BCC₁B₁与平面BED₁所成的锐二面角的大小为 $\frac{π}{3}$ ，求线段D₁E的长度．

查看试题解析
20. 已知椭圆E： $\frac{x^{2}}{a^{2}} + \frac{y^{2}}{b^{2}}$ =1（a＞b＞0）的左焦点F₁（﹣ $\sqrt{5}$ ，0），若椭圆上存在一点D，满足以椭圆短轴为直径的圆与线段DF₁相切于线段DF₁的中点F

(1)、求椭圆E的方程；

(2)、过坐标原点O的直线交椭圆W： $\frac{9 x^{2}}{2 a^{2}} + \frac{4 y^{2}}{b^{2}}$ =1于P、A两点，其中点P在第一象限，过P作x轴的垂线，垂足为C，连结AC并延长交椭圆W于B，求证：PA⊥PB．

查看试题解析
21. 已知函数 $f (x) = l n (\frac{1}{2} + \frac{1}{2} a x) + x^{2} - a x$ ．（a为常数，a＞0）
（Ⅰ）若 $x = \frac{1}{2}$ 是函数f（x）的一个极值点，求a的值；
（Ⅱ）求证：当0＜a≤2时，f（x）在 $[\frac{1}{2} ， + \infty)$ 上是增函数；
（Ⅲ）若对任意的a∈（1，2），总存在 $x_{0} \in [\frac{1}{2} ， 1]$ ，使不等式f（x₀）＞m（1﹣a²）成立，求实数m的取值范围．

查看试题解析
22. 已知直线l的极坐标方程为ρsin（θ+ $\frac{π}{4}$ ）= $\frac{\sqrt{2}}{2}$ ，圆C的参数方程为： ${\begin{matrix} x = 2 c o s θ \\ y = - 2 + 2 s i n θ \end{matrix}$ （其中θ为参数）．

(1)、判断直线l与圆C的位置关系；

(2)、若椭圆的参数方程为 ${\begin{matrix} x = 2 c o s φ \\ y = \sqrt{3} s i n φ \end{matrix}$ （φ为参数），过圆C的圆心且与直线l垂直的直线l′与椭圆相交于A，B两点，求|AB|．

查看试题解析
23. 已知函数f（x）=|2x﹣a|+a．

(1)、若不等式f（x）≤6的解集为{x|﹣2≤x≤3}，求实数a的值；

(2)、在（1）的条件下，若存在实数n使f（n）≤m﹣f（﹣n）成立，求实数m的取值范围．

查看试题解析