2017年湖北省武汉市高三五月调考数学试卷（理科）

试卷更新日期：2017-07-27 类型：高考模拟

进入出卷网下载

一、选择题

1. 已知z= $\frac{3 i}{1 - i}$ ，则复数 $\bar{z}$ 在复平面对应的点位于（）

A、第一象限 B、第二象限 C、第三象限 D、第四象限

查看试题解析
2. 设集合A={x|x＜2}，B={y|y=2^x﹣1}，则A∩B=（）

A、（﹣∞，3） B、[2，3） C、（﹣∞，2） D、（﹣1，2）

查看试题解析
3. 若实数x，y满足约束条件 ${\begin{matrix} x \geq 0 \\ y \geq 0 \\ 2 x + y \leq 2 \end{matrix}$ ，则z=x﹣2y的最大值是（）

A、2 B、1 C、0 D、﹣4

查看试题解析
4. 设{a_n}是首项为正数的等比数列，公比为q，则“q＜0”是“对任意的正整数n，a_2n_﹣1+a_2n＜0”的（）

A、充要条件 B、充分而不必要条件 C、必要而不充分条件 D、既不充分也不必要条件

查看试题解析
5. 宋元时期数学名著《算学启蒙》中有关于“松竹并生”的问题：松长五尺，竹长两尺，松日自半，竹日自倍，松竹何日而长等．下图是源于其思想的一个程序框图，若输入的a，b分别为5，2，则输出的n=（）

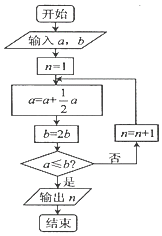A、2 B、3 C、4 D、5

查看试题解析
6. 定义在R上的函数f（x）=2^|x^﹣m|﹣1为偶函数，记a=f（log_0.53），b=f（log₂5），c=f（2m），则（）

A、a＜b＜c B、a＜c＜b C、c＜a＜b D、c＜b＜a

查看试题解析
7. 已知数列{a_n}为等差数列，S_n其前n项和，且a₂=3a₄﹣6，则S₉等于（）

A、25 B、27 C、50 D、54

查看试题解析
8. 若（3x﹣1）⁵=a₀+a₁x+a₂x²+…+a₅x⁵ ，则a₁+2a₂x+3a₃x+4a₄+5a₅=（）

A、80 B、120 C、180 D、240

查看试题解析
9. 如图是某个几何体的三视图，则该几何体的体积是（）

A、 $\sqrt{3}$ B、2 C、3 D、4

查看试题解析
10. 若存在正常数a，b，使得∀x∈R有f（x+a）≤f（x）+b恒成立，则称f（x）为“限增函数”．给出下列三个函数：①f（x）=x²+x+1；② $f (x) = \sqrt{| x |}$ ；③f（x）=sin（x²），其中是“限增函数”的是（）

A、①②③ B、②③ C、①③ D、③

查看试题解析
11. 已知函数 $f (x) = s i n (ω x + φ) (ω > 0 ， 0 < φ < \frac{π}{2}) ， f (0) = - f (\frac{π}{2})$ ，若将f（x）的图象向左平移 $\frac{π}{12}$ 个单位后所得函数的图象关于原点对称，则φ=（）

A、 $\frac{π}{12}$ B、 $\frac{π}{6}$ C、 $\frac{π}{4}$ D、 $\frac{π}{3}$

查看试题解析
12. 已知椭圆 $E ： \frac{x^{2}}{a^{2}} + \frac{y^{2}}{b^{2}} = 1 (a > b > 0)$ 内有一点M（2，1），过M的两条直线l₁ ， l₂分别与椭圆E交于A，C和B，D两点，且满足 $\vec{A M} = λ \vec{M C} ， \vec{B M} = λ \vec{M D}$ （其中λ＞0，且λ≠1），若λ变化时，AB的斜率总为 $- \frac{1}{2}$ ，则椭圆E的离心率为（）

A、 $\frac{1}{2}$ B、 $\frac{\sqrt{5} - 1}{2}$ C、 $\frac{\sqrt{2}}{2}$ D、 $\frac{\sqrt{3}}{2}$

查看试题解析

二、填空题

13. 若直线2x+y+m=0过圆x²+y²﹣2x+4y=0的圆心，则m的值为．

查看试题解析
14. 在区间[﹣1，1]内随机取两个实数x，y，则满足y≥x²﹣1的概率是．

查看试题解析
15. 棱长均相等的四面体ABCD的外接球半径为1，则该四面体ABCD的棱长为．

查看试题解析
16. 如图，在等腰三角形ABC中，已知|AB|=|AC|=1，∠A=120°，E，F分别是AB，AC上的点，且 $\vec{A E} = λ \vec{A B} ， \vec{A F} = μ \vec{A C}$ ，（其中λ，μ∈（0，1）），且λ+4μ=1，若线段EF，BC的中点分别为M，N，则 $\vec{M N}$ 的最小值为．

查看试题解析

三、解答题

17. 在△ABC中，角A，B，C的对边分别为，且满足 $\frac{2 c - b}{a} = \frac{c o s B}{c o s A}$ ．

(1)、求角A的大小；

(2)、若D为BC上一点，且 $\vec{C D} = 2 \vec{D B} ， b = 3 ， | A D | = \sqrt{21}$ ，求a．

查看试题解析
18. 如图，四棱锥P﹣ABCD中，∠ABC=∠BAD=90°，BC=2AD，△PAB与△PAD都是边长为2的等边三角形，E是BC的中点．

(1)、求证：AE∥平面PCD；

(2)、记平面PAB与平面PCD的交线为l，求二面角C﹣l﹣B的余弦值．

查看试题解析
19. 据某市地产数据研究院的数据显示，2016年该市新建住宅销售均价走势如图所示，为抑制房价过快上涨，政府从8月份采取宏观调控措施，10月份开始房价得到很好的抑制．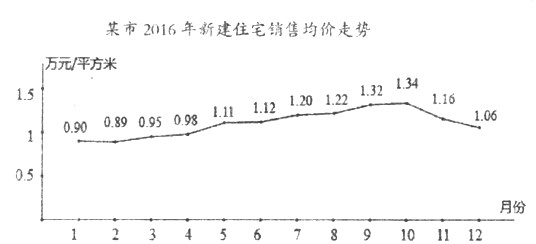
（Ⅰ）地产数据研究院研究发现，3月至7月的各月均价y（万元/平方米）与月份x之间具有较强的线性相关关系，试建立y关于x的回归方程（系数精确到0.01），政府若不调控，依次相关关系预测第12月份该市新建住宅销售均价；
（Ⅱ）地产数据研究院在2016年的12个月份中，随机抽取三个月份的数据作样本分析，若关注所抽三个月份的所属季度，记不同季度的个数为X，求X的分布列和数学期望．
参考数据： $\sum_{i = 1}^{5} x_{i}$ =25， $\sum_{i = 1}^{5} y_{i}$ =5.36， $\sum_{i = 1}^{5} (x_{i} - \bar{x}) (y_{i} - \bar{y})$ =0.64
回归方程 $\hat{y}$ = $\hat{b}$ x+ $\hat{a}$ 中斜率和截距的最小二乘估计公式分别为：
$\hat{b}$ = $\frac{\sum_{i = 1}^{n} (x_{i} - \bar{x}) (y_{i} - \bar{y})}{\sum_{i = 1}^{n} {(x_{i} - \bar{x})}^{2}}$ ， $\hat{a}$ = $\bar{y}$ ﹣ $\hat{b} \bar{x}$ ．

查看试题解析
20. 已知抛物线x²=2py（p＞0）的焦点为F，直线x=4与x轴的交点为P，与抛物线的交点为Q，且 $| Q F | = \frac{5}{4} | P Q |$ ．

(1)、求抛物线的方程；

(2)、
如图所示，过F的直线l与抛物线相交于A，D两点，与圆x²+（y﹣1）²=1相交于B，C两点（A，B两点相邻），过A，D两点分别作我校的切线，两条切线相交于点M，求△ABM与△CDM的面积之积的最小值．

查看试题解析
21. 已知函数f（x）=axln（x+1）+x+1（x＞﹣1，a∈R）．

(1)、若 $a = \frac{1}{e}$ ，求函数f（x）的单调区间；

(2)、当x≥0时，不等式f（x）≤e^x恒成立，求实数a的取值范围．

查看试题解析
22. 已知曲线C₁的参数方程为 ${\begin{matrix} x = 2 t - 1 \\ y = - 4 t - 2 \end{matrix}$ （t为参数），以原点O为极点，以x轴的正半轴为极轴建立极坐标系，曲线C₂的极坐标方程为 $ρ = \frac{2}{1 - c o s θ}$ ．
（I）求曲线C₂的直角坐标系方程；
（II）设M₁是曲线C₁上的点，M₂是曲线C₂上的点，求|M₁M₂|的最小值．

查看试题解析
23. 设函数f（x）=|x+ $\frac{8}{m}$ |+|x﹣2m|（m＞0）．
（Ⅰ）求证：f（x）≥8恒成立；
（Ⅱ）求使得不等式f（1）＞10成立的实数m的取值范围．

查看试题解析