2017年河北省衡水市高考数学一模试卷（理科）

试卷更新日期：2017-07-27 类型：高考模拟

进入出卷网下载

一、选择题

1. 已知复数z= $\frac{1 + 2 i^{3}}{2 - i}$ （i为虚数单位），则|z|=（）

A、 $\frac{3}{5}$ B、1 C、 $\frac{\sqrt{5}}{3}$ D、2

查看试题解析
2. 设p：（ $\frac{1}{2}$ ）^x＜1，q：log₂x＜0，则p是q的（）

A、充分不必要条件 B、必要不充分条件 C、充要条件 D、既不充分也不必要条件

查看试题解析
3. 执行如图程序框图，则输出结果为（）

A、5 B、4 C、3 D、2

查看试题解析
4. 现有四个函数：①y=x•sinx；②y=x•cosx；③y=x•|cosx|；④y=x•2^x的图象（部分）如图：
则按照从左到右图象对应的函数序号安排正确的一组是（）

A、①④③② B、③④②① C、④①②③ D、①④②③

查看试题解析
5. 已知sin（α+ $\frac{π}{3}$ ）+sinα=﹣ $\frac{4 \sqrt{3}}{5}$ ，﹣ $\frac{π}{2}$ ＜α＜0，则cos（α+ $\frac{2 π}{3}$ ）等于（）

A、﹣ $\frac{4}{5}$ B、﹣ $\frac{3}{5}$ C、 $\frac{4}{5}$ D、 $\frac{3}{5}$

查看试题解析
6. 某几何体的三视图如图所示，则该几何体的体积为（）

A、 $\frac{4}{3}$ B、 $\frac{5}{2}$ C、 $\frac{7}{3}$ D、 $\frac{5}{3}$

查看试题解析
7. 已知F₁、F₂分别为双曲线 $\frac{x^{2}}{a^{2}}$ ﹣ $\frac{y^{2}}{b^{2}}$ =1（a＞0，b＞0）的左、右焦点．过F₂作双曲线的渐近线的垂线，垂足为P，则|PF₁|²﹣|PF₂|²=（）

A、4a² B、4b² C、3a²+b² D、a²+3b²

查看试题解析
8. 已知函数y=2sinx的定义域为[a，b]，值域为[﹣2，1]，则b﹣a的值不可能是（）

A、 $\frac{5 π}{6}$ B、π C、2π D、 $\frac{7 π}{6}$

查看试题解析
9. 已知α，β是两个不同的平面，m，n是两条不重合的直线，则下列命题中正确的是（）

A、若m∥α，α∩β=n，则m∥n B、若m⊥α，m⊥n，则n∥α C、若m⊥α，n⊥β，α⊥β，则m⊥n D、若α⊥β，α∩β=n，m⊥n，则m⊥β

查看试题解析
10. 在△ABC中，内角A，B，C所对的边分别为a，b，c，A= $\frac{π}{4}$ ，b²﹣a²= $\frac{1}{2} c^{2}$ ，则tanC=（）

A、2 B、﹣2 C、 $\frac{1}{2}$ D、﹣ $\frac{1}{2}$

查看试题解析
11. 设F为抛物线y²=4x的焦点，A，B，C为该抛物线上不同的三点， $\vec{F A}$ + $\vec{F B}$ + $\vec{F C}$ = $\vec{0}$ ，O为坐标原点，且△OFA、△OFB、△OFC的面积分别为S₁、S₂、S₃ ，则S₁²+S₂²+S₃²=（）

A、2 B、3 C、6 D、9

查看试题解析
12. 定义：如果函数f（x）在[a，b]上存在x₁ ， x₂（a＜x₁＜x₂＜b）满足 $f' (x_{1}) = \frac{f (b) - f (a)}{b - a}$ ， $f' (x_{2}) = \frac{f (b) - f (a)}{b - a}$ ，则称函数f（x）是[a，b]上的“双中值函数”．已知函数f（x）=x³﹣x²+a是[0，a]上的“双中值函数”，则实数a的取值范围是（）

A、 $(\frac{1}{3} ， \frac{1}{2})$ B、（ $\frac{3}{2} ， 3$ ） C、（ $\frac{1}{2}$ ，1） D、（ $\frac{1}{3}$ ，1）

查看试题解析

二、填空题

13. 甲、乙、丙三人投掷飞镖，他们的成绩（环数）如下面的频数条统计图所示．则甲、乙、丙三人的训练成绩方差S_甲² ， S_乙² ， S_丙²的大小关系是．

查看试题解析
14. 安排甲、乙、丙、丁四人参加周一至周五的公益活动，每天只需一人参加，其中甲参加三天活动，甲、乙、丙、丁每人参加一天，那么甲连续三天参加活动的概率为．

查看试题解析
15. 如图，直角梯形ABCD中，AB∥CD，∠DAB=90°，AD=AB=4，CD=1，动点P在边BC上，且满足 $\vec{A P} = m \vec{A B} + n \vec{A D}$ （m，n均为正实数），则 $\frac{1}{m} + \frac{1}{n}$ 的最小值为．

查看试题解析
16. 已知函数 $f (x) = {\begin{matrix} 3^{x} ， x \in [0 ， 1] \\ \frac{9}{2} - \frac{3}{2} x ， x \in (1 ， 3] \end{matrix}$ 当t∈[0，1]时，f（f（t））∈[0，1]，则实数t的取值范围是．

查看试题解析

三、解答题

17. 已知数列{a_n}的前n项和为S_n ， a₁=2，且满足 $a_{n + 1} = S_{n} + 2^{n + 1}$ （n∈N^*）．
（Ⅰ）证明数列 ${\frac{S_{n}}{2^{n}}}$ 为等差数列；
（Ⅱ）求S₁+S₂+…+S_n ．

查看试题解析
18. 如图（1），等腰直角三角形ABC的底边AB=4，点D在线段AC上，DE⊥AB于E，现将△ADE沿DE折起到△PDE的位置（如图（2））．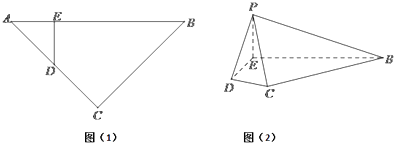
（Ⅰ）求证：PB⊥DE；
（Ⅱ）若PE⊥BE，直线PD与平面PBC所成的角为30°，求PE长．

查看试题解析
19. 4月23人是“世界读书日”，某中学在此期间开展了一系列的读书教育活动，为了解本校学生课外阅读情况，学校随机抽取了100名学生对其课外阅读时间进行调查，下面是根据调查结果绘制的学生日均课外阅读时间（单位：分钟）的频率分布直方图，若将日均课外阅读时间不低于60分钟的学生称为“读书谜”，低于60分钟的学生称为“非读书谜”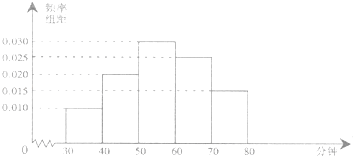

(1)、根据已知条件完成下面2×2的列联表，并据此判断是否有99%的把握认为“读书谜”与性别有关？
非读书迷
读书迷
合计
男
15
女
45
合计

(2)、将频率视为概率，现在从该校大量学生中，用随机抽样的方法每次抽取1人，共抽取3次，记被抽取的3人中的“读书谜”的人数为X，若每次抽取的结果是相互独立的，求X的分布列，期望E（X）和方程D（X）
附：K²= $\frac{n {(a d - b c)}^{2}}{(a + b) (c + d) (a + c) (b + d)}$ n=a+b+c+d
P（K²≥k₀）
0.100
0.050
0.025
0.010
0.001
k₀
2.706
3.841
5.024
6.635
10.828

查看试题解析
20. 已知两动圆F₁：（x+ $\sqrt{3}$ ）²+y²=r²和F₂：（x﹣ $\sqrt{3}$ ）²+y²=（4﹣r）²（0＜r＜4），把它们的公共点的轨迹记为曲线C，若曲线C与y轴的正半轴的交点为M，且曲线C上的相异两点A、B满足： $\vec{M A}$ • $\vec{M B}$ =0．

(1)、求曲线C的方程；

(2)、证明直线AB恒经过一定点，并求此定点的坐标；

(3)、求△ABM面积S的最大值．

查看试题解析
21. 设函数f（x）= $\frac{b x}{l n x}$ ﹣ax，e为自然对数的底数
（Ⅰ）若函数f（x）的图象在点（e² ， f（e²））处的切线方程为 3x+4y﹣e²=0，求实数a，b的值；
（Ⅱ）当b=1时，若存在 x₁ ， x₂∈[e，e²]，使 f（x₁）≤f′（x₂）+a成立，求实数a的最小值．

查看试题解析

P（K²≥k₀）	0.100	0.050	0.025	0.010	0.001
k₀	2.706	3.841	5.024	6.635	10.828

	非读书迷	读书迷	合计
男		15
女			45
合计