2017年贵州省贵阳市高考数学二模试卷（理科）

试卷更新日期：2017-07-27 类型：高考模拟

进入出卷网下载

一、选择题

1. 设i为虚数单位，若复数 $\frac{z}{- i}$ 在复平面内对应的点为（1，2），则z=（）

A、﹣2+i B、2﹣i C、﹣1+2i D、1﹣2i

查看试题解析
2. A、B为两个非空集合，定义集合A﹣B={x|x∈A且x∉B}，若A={﹣2，﹣1，0，1，2}，B={x|（x﹣1）（x+2）＜0}，则A﹣B=（）

A、{2} B、{1，2} C、{﹣2，1，2} D、{﹣2，﹣1，0}

查看试题解析
3. 已知向量 $\vec{a}$ ， $\vec{b}$ ，| $\vec{a}$ |=2，| $\vec{b}$ |=1，若 $\vec{b}$ •（ $\vec{b}$ ﹣ $\vec{a}$ ）=2，则向量 $\vec{a}$ 与 $\vec{b}$ 的夹角为（）

A、 $\frac{5 π}{6}$ B、 $\frac{2 π}{3}$ C、 $\frac{π}{3}$ D、 $\frac{π}{6}$

查看试题解析
4. 已知函数f（x）=1n（x+2）+1n（x﹣2），则f（x）是（）

A、奇函数 B、偶函数 C、既是奇函数又是偶函数 D、非奇非偶函数

查看试题解析
5. 某程序框图如图所示，则该程序运行后输出的值是（）

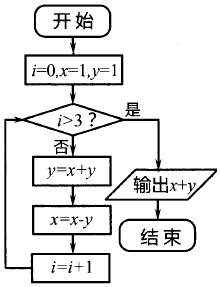A、0 B、﹣1 C、﹣2 D、﹣8

查看试题解析
6. 在平面直角坐标系中，角α的顶点与原点O重合，始边与x轴的非负半轴重合，点P（﹣2t，t）（t≠0）是角α终边上的一点，则 $t a n (α + \frac{π}{4})$ 的值为（）

A、 $3 - 2 \sqrt{2}$ B、3 C、 $- \frac{1}{3}$ D、 $\frac{1}{3}$

查看试题解析
7. 若 ${(x - \frac{a}{x})}^{5}$ 的展示式中x³的系数为30，则实数a=（）

A、﹣6 B、6 C、﹣5 D、5

查看试题解析
8. 已知实数x、y满足 ${\begin{matrix} 1 \leq x - y \leq 2 \\ 2 \leq x + y \leq 4 \end{matrix}$ ，则z=4x﹣2y的最大值为（）

A、3 B、5 C、10 D、12

查看试题解析
9. 某几何体的三视图如图所示，则该几何体的体积为（）

A、16π﹣ $\frac{16}{3}$ B、16π﹣ $\frac{32}{3}$ C、8π﹣ $\frac{16}{3}$ D、8π﹣ $\frac{32}{3}$

查看试题解析
10. 已知椭圆E： $\frac{x^{2}}{a^{2}} + \frac{y^{2}}{b^{2}}$ =1（a＞b＞0）与两条平行直线l₁：y=x+b与l₂：y=x﹣b分别相交于四点A，B，D，C，且四边形ABCD的面积为 $\frac{8 b^{2}}{3}$ ，则椭圆E的离心率为（）

A、 $\frac{\sqrt{2}}{2}$ B、 $\frac{\sqrt{3}}{2}$ C、 $\frac{\sqrt{2}}{3}$ D、 $\frac{\sqrt{3}}{3}$

查看试题解析
11. 富华中学的一个文学兴趣小组中，三位同学张博源、高家铭和刘雨恒分别从莎士比亚、雨果和曹雪芹三位名家中选择了一位进行性格研究，并且他们选择的名家各不相同．三位同学一起来找图书管理员刘老师，让刘老师猜猜他们三人各自的研究对象．刘老师猜了三句话：“①张博源研究的是莎士比亚；②刘雨恒研究的肯定不是曹雪芹；③高家铭自然不会研究莎士比亚．”很可惜，刘老师的这种猜法，只猜对了一句，据此可以推知张博源、高家铭和刘雨恒分别研究的是（）

A、曹雪芹、莎士比亚、雨果 B、雨果、莎士比亚、曹雪芹 C、莎士比亚、雨果、曹雪芹 D、曹雪芹、雨果、莎士比亚

查看试题解析
12. 已知函数f（x）=x² ， g（x）=﹣1nx，g'（x）为g（x）的导函数．若存在直线l同为函数f（x）与g'（x）的切线，则直线l的斜率为（）

A、 $2 \sqrt{5} - 4$ B、2 C、4 D、 $\frac{1}{2}$

查看试题解析

二、填空题

13. 定积分 $\int_{0}^{1} (x^{2} + e^{x} - \frac{1}{3}) d x$ 的值为．

查看试题解析
14. 在△ABC中，A，B，C的对边分别是a，b，c，若c²=acosB+bcosA，a=b=3，则△ABC的周长为．

查看试题解析
15. 从集合{2，3，4，5}中随机抽取一个数a，从集合{4，6，8}中随机抽取一个数b，则向量 $\vec{m}$ =（a，b）与向量 $\vec{n}$ =（﹣2，1）垂直的概率为．

查看试题解析
16. 已知等腰直角△ABC的斜边BC=2，沿斜边的高线AD将△ABC折起，使二面角B﹣AD﹣C为 $\frac{π}{3}$ ，则四面体ABCD的外接球的表面积为．

查看试题解析

三、解答题：解答应写出文字说明、证明过程或演算步骤．

17. 设S_n是数列{a_n}的前n项和，a_n＞0，且4S_n=a_n（a_n+2）．
（Ⅰ）求数列{a_n}的通项公式；
（Ⅱ）设b_n= $\frac{1}{(a_{n} - 1) (a_{n} + 1)}$ ，T_n=b₁+b₂+…+b_n ，求证：T_n＜ $\frac{1}{2}$ ．

查看试题解析
18. 医学上某种还没有完全攻克的疾病，治疗时需要通过药物控制其中的两项指标H和V．现有..三种不同配方的药剂，根据分析，A，B，C三种药剂能控制H指标的概率分别为0.5，0.6，0.75，能控制V指标的概率分别是0.6，0.5，0.4，能否控制H指标与能否控制V指标之间相互没有影响．
（Ⅰ）求A，B，C三种药剂中恰有一种能控制H指标的概率；
（Ⅱ）某种药剂能使两项指标H和V都得到控制就说该药剂有治疗效果．求三种药剂中有治疗效果的药剂种数X的分布列．

查看试题解析
19. 如图，棱柱ABCD﹣A₁B₁C₁D₁中，底面ABCD是平行四边形，侧棱AA₁⊥底面ABCD，AB=1，AC= $\sqrt{3}$ ，BC=BB₁=2．
（Ⅰ）求证：AC⊥平面ABB₁A₁；
（Ⅱ）求二面角A﹣C₁D﹣C的平面角的余弦值．

查看试题解析
20. 已知椭圆C： $\frac{x^{2}}{a^{2}} + \frac{y^{2}}{7 - a^{2}}$ =1（a＞0）的焦点在x轴上，且椭圆C的焦距为2．
（Ⅰ）求椭圆C的标准方程；
（Ⅱ）过点R（4，0）的直线l与椭圆C交于两点P，Q，过P作PN⊥x轴且与椭圆C交于另一点N，F为椭圆C的右焦点，求证：三点N，F，Q在同一条直线上．

查看试题解析
21. 已知函数f（x）=（x²﹣2x）1nx+ax²+2，g（x）=f（x）﹣x﹣2．
（Ⅰ）当a=﹣1时，求f（x）在（1，f（1））处的切线方程；
（Ⅱ）若a＞0且函数g（x）有且仅有一个零点，求实数a的值；
（Ⅲ）在（Ⅱ）的条件下，若e^﹣2＜x＜e时，g（x）≤m恒成立，求实数m的取值范围．

查看试题解析
22. 在平面直角坐标系xOy中，曲线C的参数方程为 ${\begin{matrix} x = 4 t^{2} \\ y = 4 t \end{matrix}$ （t为参数），以O为极点x轴的正半轴为极轴建极坐标系，直线l的极坐标方程为ρ（cosθ﹣sinθ）=4，且与曲线C相交于A，B两点．
（Ⅰ）在直角坐标系下求曲线C与直线l的普通方程；
（Ⅱ）求△AOB的面积．

查看试题解析
23. 已知函数f（x）=m﹣|x﹣1|，（m＞0），且f（x+1）≥0的解集为[﹣3，3]．
（Ⅰ）求m的值；
（Ⅱ）若正实数a，b，c满足 $\frac{1}{a} + \frac{1}{2 b} + \frac{1}{3 c} = m$ ，求证：a+2b+3c≥3．

查看试题解析