2017年山西省省际名校高考数学押题卷（理科）

试卷更新日期：2017-07-27 类型：高考模拟

进入出卷网下载

一、选择题

1. 已知集合A={x|（x﹣1）（x﹣3）（x﹣5）＜0}，B={x∈N|﹣2＜x＜6}，则A∩B的元素的个数为（）

A、1 B、2 C、3 D、4

查看试题解析
2. 设i为虚数中单位，若复数z= $\frac{a}{1 - 2 i}$ +i（a∈R）的实部与虚部互为相反数，则a=（）

A、﹣ $\frac{5}{3}$ B、﹣ $\frac{1}{3}$ C、﹣1 D、﹣5

查看试题解析
3. 为了解甲、乙两厂产品的质量，从甲厂生产的产品中随机抽取3件样品，从乙厂生产的产品中随机抽取4件样品，测量产品中某种元素的含量（单位：毫克），如图是测量数据的茎叶图．若它们的中位数相同，平均数也相同，则图中的m，n的比值 $\frac{m}{n}$ =（）

A、1 B、 $\frac{1}{3}$ C、 $\frac{8}{3}$ D、 $\frac{3}{8}$

查看试题解析
4. 对于两个不重合的平面α与β，给定下列条件，其中可以判定α与β平行的条件是（）

A、α内有不共线的三点到β的距离相等； B、a内存在直线平行于平面β C、存在平面γ，使得α⊥γ，β⊥γ D、存在异面直线l，m使得l∥α，l∥β，m∥α，m∥β

查看试题解析
5. 执行如图所示的程序框图，则输出S的值为（）

A、 $\frac{5}{6}$ B、 $\frac{4}{5}$ C、 $\frac{6}{7}$ D、 $\frac{7}{8}$

查看试题解析
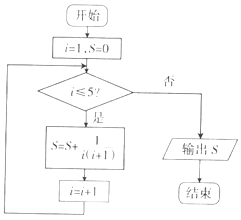6. 下列命题中的真命题为（）

A、若向量 $\vec{a}$ ∥ $\vec{b}$ ，则存在唯一的实数λ，使得 $\vec{a}$ =λ $\vec{b}$ B、已知随机变量ξ服从正态分布N（1，σ²），若P（ξ≤4）=0.79，则P（ξ≤﹣2）=0.21 C、“φ= $\frac{3 π}{2}$ ”是“y=sin（2x+φ）为偶函数”的充要条件 D、函数y=f（1+x）与函数y=f（1﹣x）的图象关于直线x=1对称

查看试题解析
7. 已知向量 $\vec{a}$ =（x﹣1，3）， $\vec{b}$ =（1，y），其中x，y都为正实数，若 $\vec{a} ⊥ \vec{b}$ ，则 $\frac{1}{x} + \frac{1}{3 y}$ 的最小值为（）

A、2 B、2 $\sqrt{2}$ C、4 D、2 $\sqrt{3}$

查看试题解析
8. 已知在△ABC中，b²+a²﹣c²＜0，且b＞a，sinA+ $\sqrt{2}$ cosA= $\frac{5}{3}$ ，则tanA=（）

A、 $\frac{2 \sqrt{2}}{3}$ 或 $\frac{4 \sqrt{2}}{9}$ B、 $\frac{\sqrt{2}}{4}$ C、 $\frac{7 \sqrt{2}}{8}$ D、 $\frac{\sqrt{2}}{4}$ 或 $\frac{7 \sqrt{2}}{8}$

查看试题解析
9. 某班上午有五节课，分別安排语文，数学．英语．物理、化学各一节课．要求语文与化学相邻，数学与物理不相邻．且数学课不排第一节，则不同排课法的种数是（）

A、16 B、24 C、8 D、12

查看试题解析
10. 已知F₁ ， F₂分别是椭圆mx²+y²=m（0＜m＜1）的左、右焦点，P为椭圆上任意一点，若 $\frac{| \vec{P F_{2}} |^{2} + | \vec{P F_{1}} |}{| \vec{P F_{1}} |}$ 的最小值为 $\frac{4}{3}$ ，则椭圆的离心率是（）

A、 $\frac{1}{2}$ B、 $\frac{1}{3}$ C、 $\frac{1}{4}$ D、 $\frac{1}{5}$

查看试题解析
11. 设I是△ABC的内心，其中AB=4，BC=6，AC=5，且 $\vec{A I}$ =m $\vec{A B}$ +n $\vec{A C}$ ，则曲线y=（m﹣n）x²的焦点坐标为（）

A、（﹣ $\frac{1}{60}$ ，0） B、（0， $\frac{15}{4}$ ） C、（0，﹣ $\frac{15}{4}$ ） D、（ $\frac{1}{60}$ ，0）

查看试题解析
12. 已知函数f（x）=（ $\frac{1}{3}$ x³﹣x²+ $\frac{2}{3}$ ）cos²⁰¹⁷（ $\frac{π}{3} x$ + $\frac{2 π}{3}$ ）+2x+3在[﹣2015，2017]上的最大值为M，最小值为m，则M+m=（）

A、5 B、10 C、1 D、0

查看试题解析

二、填空题

13. 若幂函数y=（m²﹣4m+1）x^m2^﹣^2m^﹣³为（0，+∞）上的增函数，则实数m的值等于．

查看试题解析
14. 在（2^x﹣3）⁵•（4^﹣^x﹣1）的展开式中含（2^x）²的项为．

查看试题解析
15. 《九章算术》是东方数学思想之源，在卷五《商功》中有以下问题：今有羡除，下广六尺，上广一丈，深三尺，末广八尺，无深，袤七尺，问积几何？译文：如图所示的几何体是三个侧面皆为等腰梯形，其他两面为直角三角形的五面体，（前端）下宽6尺，上宽一丈，深3尺，末端宽8尺，无深，长7尺，则它的体积是立方尺．

查看试题解析
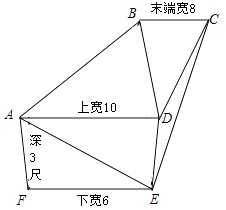16. 已知数列{a_n}中，a₁=﹣l，a_n₊₁=2a_n+（3n﹣1）•3ⁿ⁺¹ ，（n∈N^*），则其通项a_n= ．

查看试题解析

三、解答题

17. 已知在△ABC中，内角A，B，C的对边分别为a，b，c，cosA= $\frac{4 \sqrt{3}}{3}$ sin²C﹣cos（B﹣C），且 $\frac{π}{2}$ 是A与3C的等差中项

(1)、求tanB的值

(2)、若b=2 $\sqrt{2}$ ，求三角形△ABC的面积．

查看试题解析
18. 为弘扬中国传统文化，2017年中央电视台著名主持人董卿主持了一档节目《中国诗词大会》参赛的100名选手年龄分布情况如下：
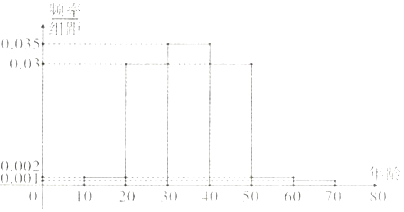
（Ⅰ）根据频率分布直方图，估计这组数据的中位数和平均值 $\bar{x}$ （保留1位小数）
（Ⅱ）节目最后由高中生武亦姝和编辑彭敏争夺冠军，比赛规定：主持人每出一题，两位选手必有一人得1分，另一人不得分，先得5分者将成为第二季的总冠军，现比赛进行到武亦姝和彭敏的得分比为3：2，接下来假设主持人每出一道题，彭敏得分的概率为 $\frac{3}{5}$ ，武亦姝得分的概率为 $\frac{2}{5}$ ，请问最终武亦姝获得冠军的概率是多少？
（Ⅲ）现从年龄在[10，20）、[50，60），[60，70]内的三组选手中任意抽取2人，求抽出选手中年龄大于50岁的人数ξ的概率分布列和期望．

查看试题解析
19. 已知如图所示的几何体中，四边形ABCD是边长为2的菱形，面PBC⊥面A BCD，点E是AD 的中点，PQ∥面ABCD且点Q在面ABCD上的射影Q′落在AB的延长线上，若PQ=1，PB= $\sqr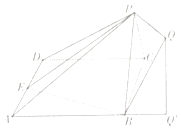t{2}$ ，且（ $\vec{P B} + \vec{P C}$ ）• $\vec{B C}$ =0， $\vec{A B} \cdot \vec{A D}$ =2
（Ⅰ）求证面PBC⊥面PBE
（Ⅱ）求平面PBQ与平面PAD所成钝二面角的正切值．

查看试题解析
20. 已知椭圆E： $\frac{x^{2}}{a^{2}} + \frac{y^{2}}{b^{2}}$ =1（a＞b＞0）的离心率为 $\frac{\sqrt{3}}{2}$ 直线MN与圆x²+y²= $\frac{4}{5}$ 相切，M（a，0），N（0，b）
（Ⅰ）求E的方程；
（Ⅱ）若E的右焦点为F，圆x²+y²=1的切线AB与E交于A，B 两点（A，B均在y轴右侧），求证：△ABF的周长为定值，并求△ABF的内切圆半径的最大值．

查看试题解析
21. 已知函数f（x）=2lnx，g（x）= $\frac{1}{2}$ ax²+（2a﹣1）x
（Ⅰ）设h（x）=f（x）﹣g（x），讨论函数h（x）的单调区间；
（Ⅱ）若f（x）﹣ax=0有两个不同实数解x₁ ， x₂ ，求证：lnx₁+lnx₂＞2．

查看试题解析
22. 在直角坐标系xOy中，直线l的参数方程 ${\begin{matrix} x = 1 + t \\ y = - t \end{matrix}$ （t为参数）以O为极点，x轴的非负半轴为极轴建立极坐标系，曲线C的极坐标方程ρ+2rcosθ=0（r＞0）．
（I ）求直线l的普通方程和曲线C的直角坐标方程；
（Ⅱ）当r为何值时，曲线C 上有且只有3个点到直线l的距离为1？

查看试题解析
23. 设函数f（x）=2|x+1|+|x﹣3|．

(1)、求不等式f（x）＜5的解集；

(2)、设g（x）=kx，若f（x）≥g（x）恒成立，求k的取值范围．

查看试题解析