2017年山西省晋中市祁县高考数学模拟试卷（理科）（5月份）

试卷更新日期：2017-07-27 类型：高考模拟

进入出卷网下载

一、选择题

1. 若集合A={x|y= $x^{\frac{1}{2}}$ }，B={x|y=ln（x+1）}，则A∩B=（）

A、[0，+∞） B、（0，1） C、（﹣1，+∞） D、（﹣∞，﹣1）

查看试题解析
2. 下面是关于复数z=2﹣i的四个命题：p₁：|z|=5；p₂：z²=3﹣4i；p₃：z的共轭复数为﹣2+i；p₄：z的虚部为﹣1，其中真命题为（）

A、p₂ ， p₃ B、p₁ ， p₂ C、p₂ ， p₄ D、p₃ ， p₄

查看试题解析
3. 已知函数f（x）= ${\begin{matrix} f (x + 2) ， x < 3 \\ {(\frac{1}{2})}^{x} ， x \geq 3 \end{matrix}$ ，则f（﹣4）=（）

A、 $\frac{1}{16}$ B、 $\frac{1}{8}$ C、 $\frac{1}{4}$ D、 $\frac{1}{2}$

查看试题解析
4. 现有4张卡片，正面分别标有1，2，3，4，背面完全相同．将卡片洗匀，背面向上放置，甲、乙二人轮流抽取卡片，每人每次抽取一张，抽取后不放回，甲先抽．若二人约定，先抽到标有偶数的卡片者获胜，则甲获胜的概率是（）

A、 $\frac{5}{12}$ B、 $\frac{1}{2}$ C、 $\frac{7}{12}$ D、 $\frac{2}{3}$

查看试题解析
5. 定义： $| \begin{matrix} a & b \\ c & d \end{matrix} | = a d - b c$ ，如 $| \begin{matrix} 1 & 2 \\ 3 & 4 \end{matrix} | = 1 \times 4 - 2 \times 3 = - 2$ ，则 $| \begin{matrix} \int_{1}^{2} x d x & 3 \\ 1 & 2 \end{matrix} |$ =（）

A、0 B、 $\frac{3}{2}$ C、3 D、6

查看试题解析
6. 在（1+x）+（1+x）²+（1+x）³+…+（1+x）¹¹的展开式中，x²的系数是（）

A、55 B、66 C、165 D、220

查看试题解析
7. 某程序框图如图所示，则该程序运行后输出的B=（）

A、15 B、29 C、31 D、63

查看试题解析
8. 在△ABC中，角A、B、C所对的边分别为a，b，c，已知a=1，b= $\sqrt{3}$ ，A=30°，B为锐角，那么角A：B：C的比值为（）

A、1：1：3 B、1：2：3 C、1：3：2 D、1：4：1

查看试题解析
9. 某几何体的三视图如图所示，则该几何体的表面积是（）

A、 $20 + 4 \sqrt{5}$ B、 $12 + 4 \sqrt{5}$ C、 $20 + 2 \sqrt{5}$ D、 $12 + 2 \sqrt{5}$

查看试题解析
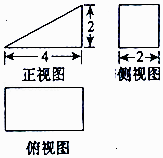10. 已知A，B是半径为 $2 \sqrt{3}$ 的球面上的两点，过AB作互相垂直的两个平面α、β，若α，β截该球所得的两个截面的面积之和为16π，则线段AB的长度是（）

A、 $\sqrt{2}$ B、2 C、 $2 \sqrt{2}$ D、4

查看试题解析
11. P为双曲线 $x^{2} - \frac{y^{2}}{15} = 1$ 右支上一动点，M、N分别是圆（x+4）²+y²=4和圆（x﹣4）²+y²=1上的点，则|PM|﹣|PN|的最大值为（）

A、5 B、6 C、7 D、4

查看试题解析
12. 若关于x的不等式x（1+lnx）+2k＞kx的解集为A，且（2，+∞）⊆A，则整数k的最大值是（）

A、3 B、4 C、5 D、6

查看试题解析

二、填空题

13. 已知实数x，y满足不等式组 ${\begin{matrix} 1 \leq x + y \leq 2 \\ - 1 \leq x - y \leq 1 \end{matrix}$ ，则z= $\frac{y + 1}{x + 1}$ 的最大值是．

查看试题解析
14. 已知 $s i n θ + c o s θ = \frac{1}{5}$ ， $θ \in (\frac{π}{2} ， π)$ ，则tanθ= ．

查看试题解析
15. 直线x=a分别与曲线y=2x+1，y=x+lnx交于A，B，则|AB|的最小值为．

查看试题解析
16. 如图，已知正方体ABCD﹣A₁B₁C₁D₁的棱长为2，点E为线段A₁B₁的中点，点F，G分别是线段A₁D与BC₁上的动点，当三棱锥E﹣FGC的俯视图的面积最大时，该三棱锥的正视图的面积是．

查看试题解析

三、解答题

17. 数列{a_n}满足a_n+5a_n₊₁=36n+18，n∈N^* ，且a₁=4．

(1)、写出{a_n}的前3项，并猜想其通项公式；

(2)、用数学归纳法证明你的猜想．

查看试题解析

18. 某印刷厂为了研究印刷单册书籍的成本y（单位：元）与印刷册数x（单位：千册）之间的关系，在印制某种书籍时进行了统计，相关数据见下表：

印刷册数（千册）	2	3	4	5	8
单册成本（元）	3.2	2.4	2	1.9	1.7

根据以上数据，技术人员分别借助甲、乙两种不同的回归模型，得到两个回归方程，方程甲： ${\overset{\land}{y}}^{(1)}$ = $\frac{4}{x} + 1.1$ ，方程乙： $\overset{\land^{(2)}}{y}$ = $\frac{6.4}{x^{2}} + 1.6$ ．

(1)、为了评价两种模型的拟合效果，完成以下任务．

①完成下表（计算结果精确到0.1）；

印刷册数x（千册）		2	3	4	5	8
单册成本y（元）		3.2	2.4	2	1.9	1.7
模型甲	估计值 ${\overset{\land}{y_{i}}}^{(1)}$		2.4	2.1		1.6
模型甲	残差 ${\overset{\land}{e_{i}}}^{(1)}$		0	﹣0.1		0.1
模型乙	估计值 ${\overset{\land}{y_{i}}}^{(2)}$		2.3	2	1.9
模型乙	残差 ${\overset{\land}{e_{i}}}^{(2)}$		0.1	0	0

②分别计算模型甲与模型乙的残差平方和Q₁及Q₂ ，并通过比较Q₁ ， Q₂的大小，判断哪个模型拟合效果更好．

(2)、该书上市之后，受到广大读者热烈欢迎，不久便全部售罄，于是印刷厂决定进行二次印刷．根据市场调查，新需求量为8千册（概率0.8）或10千册（概率0.2），若印刷厂以每册5元的价格将书籍出售给订货商，问印刷厂二次印刷8千册还是10千册能获得更多利润？（按（1）中拟合效果较好的模型计算印刷单册书的成本）

查看试题解析

19. 如图，在正三棱柱ABC﹣A₁B₁C₁中，点E，F分别是棱CC₁ ， BB₁上的点，且EC=2FB．
（Ⅰ）证明：平面AEF⊥平面ACC₁A₁；
（Ⅱ）若AB=EC=2，求二面角C﹣AF﹣E的余弦值．

查看试题解析
20. 已知椭圆C的中心在原点，焦点在x轴上，离心率 $e < \frac{\sqrt{2}}{2}$ ．以两个焦点和短轴的两个端点为顶点的四边形的周长为8，面积为 $2 \sqrt{3}$ ．
（Ⅰ）求椭圆C的方程；
（Ⅱ）若点P（x₀ ， y₀）为椭圆C上一点，直线l的方程为3x₀x+4y₀y﹣12=0，求证：直线l与椭圆C有且只有一个交点．

查看试题解析
21. 设函数 $f (x) = m l n x + \frac{n}{x}$ ，曲线y=f（x）在点（1，f（1））处的切线方程为y=x﹣1．
（Ⅰ）求实数m，n的值；
（Ⅱ）若b＞a＞1， $A = f (\frac{a + b}{2})$ ， $B = \frac{f (a) + f (b)}{2}$ ， $C = \frac{b f (b) - a f (a)}{b - a} - 1$ ，试判断A，B，C三者是否有确定的大小关系，并说明理由．

查看试题解析
22. 已知直线l： ${\begin{matrix} x = 1 + t c o s α \\ y = t s i n α \end{matrix}$ （其中t为参数，α为倾斜角）．以坐标原点O为极点，x轴的正半轴为极轴，建立极坐标系，曲线C的极坐标方程为ρ= $\frac{c o s θ}{s i n^{2} θ}$ ．

(1)、求C的直角坐标方程，并求C的焦点F的直角坐标；

(2)、已知点P（1，0），若直线l与C相交于A，B两点，且 $\frac{1}{| P A |} + \frac{1}{| P B |}$ =2，求△FAB的面积．

查看试题解析
23. 已知函数f（x）=|x+2|+|x﹣2|．

(1)、求不等式f（x）≤6的解集A；

(2)、若m，n∈A，试证：| $\frac{1}{3}$ m﹣ $\frac{1}{2}$ n|≤ $\frac{5}{2}$ ．

查看试题解析