2017年辽宁省部分重点中学协作体高考数学模拟试卷（理科）（5月份）

试卷更新日期：2017-07-27 类型：高考模拟

进入出卷网下载

一、选择题

1. 设集合A={x∈N|lgx≤1}，B={x|x²＜16}，则A∩B=（）

A、（﹣∞，4） B、（0，4） C、{0，1，2，3} D、{1，2，3}

查看试题解析
2. 设i为虚数单位，若复数z满足z• $\frac{{(1 + i)}^{2}}{2}$ =1+2i，则复数z的虚部为（）

A、﹣1 B、﹣i C、﹣2 D、﹣2i

查看试题解析
3. 某观察者站在点O观察练车场上匀速行驶的小车P的运动情况，小车从点A出发的运动轨迹如图所示．设观察者从点A开始随动点P变化的视角为θ=∠AOP（＞0），练车时间为t，则函数θ=f（t）的图象大致为（）

A、 B、 C、 D、

查看试题解析
4. 一个几何体的三视图如图所示（其中主视图的弧线为四分之一圆周），则该几何体的体积为（）

A、64﹣4π B、64+6π C、48+4π D、64﹣6π

查看试题解析
5. 设直角坐标系xOy平面内的三点A（1，﹣2），B（a，﹣1），C（﹣b，0）．其中a＞0，b＞0．若A，B，C三点共线．则 $\frac{1}{a}$ + $\frac{2}{b}$ 的最小值为（）

A、4 B、6 C、8 D、9

查看试题解析
6. 宋元时期数学名著《算学启蒙》中有关于“松竹并生”的问题：松长五尺，竹长两尺，松日自半，竹日自倍，松竹何日而长等．下图是源于其思想的一个程序框图，若输入的a，b分别为5，2，则输出的n=（）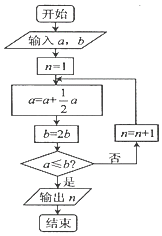

A、2 B、3 C、4 D、5

查看试题解析
7. 已知函数f（x）=asinx+bcosx（x∈R），若x=x₀是函数f（x）的一条对称轴，且tanx₀=3，则点（a，b）所在的直线为（）

A、x﹣3y=0 B、x+3y=0 C、3x﹣y=0 D、3x+y=0

查看试题解析
8. 正四面体ABCD的棱长为4，E为棱AB的中点，过E作此正四面体的外接球的截面，则截面面积的最小值是（）

A、4π B、8π C、12π D、16π

查看试题解析
9. 定义 $\frac{n}{P_{1} + P_{2} + \dots + P_{n}}$ 为n个正数P₁ ， P₂…P_n的“均倒数”，若已知正整数数列{a_n}的前n项的“均倒数”为 $\frac{1}{2 n + 1}$ ，又b_n= $\frac{a_{n} + 1}{4}$ ，则 $\frac{1}{b_{1} b_{2}}$ + $\frac{1}{b_{2} b_{3}}$ +…+ $\frac{1}{b_{10} b_{11}}$ =（）

A、 $\frac{1}{11}$ B、 $\frac{1}{12}$ C、 $\frac{10}{11}$ D、 $\frac{11}{12}$

查看试题解析
10. 如果一个n位十进制数 $\bar{a_{1} a_{2 \dots} a_{n}}$ 的数位上的数字满足“小大小大…小大”的顺序，即满足：a₁＜a₂＞a₃＜a₄＞a₅＜a₆…，我们称这种数为“波浪数”；从1，2，3，4，5组成的数字不重复的五位数中任取一个五位数 $\bar{a b c d e}$ ，这个数为“波浪数”的概率是（）

A、 $\frac{1}{10}$ B、 $\frac{2}{15}$ C、 $\frac{1}{5}$ D、 $\frac{4}{15}$

查看试题解析
11. 已知f（x）是定义在R上的函数，且满足①f（4）=0；②曲线y=f（x+1）关于点（﹣1，0）对称；③当x∈（﹣4，0）时f（x）=log₂（ $\frac{x}{e^{| x |}}$ +e^x﹣m+1），若y=f（x）在x∈[﹣4，4]上有5个零点，则实数m的取值范围为（）

A、[﹣3e^﹣⁴ ， 1） B、[﹣3e^﹣⁴ ， 1）∪{﹣e^﹣²} C、[0，1）∪{﹣e^﹣²} D、[0，1）

查看试题解析
12. 已知正三角形ABC的顶点A，B在抛物线y²=4x上，另一个顶点C（4，0），则这样的正三角形有（）

A、1个 B、2个 C、3个 D、4个

查看试题解析

二、填空题

13. 若向量 $\vec{a}$ ， $\vec{b}$ 满足：| $\vec{a}$ |=1，（ $\vec{a}$ + $\vec{b}$ ）⊥ $\vec{a}$ ，（2 $\vec{a}$ + $\vec{b}$ ）⊥ $\vec{b}$ ，则| $\vec{b}$ |= ．

查看试题解析
14. 若（2x+ $\sqrt{3}$ ）⁴=a₀+a₁x+a₂x²+a₃x³+a₄x⁴ ，则（a₀+a₂+a₄）²﹣（a₁+a₃）²的值为．

查看试题解析
15. 某校今年计划招聘女教师x人，男教师y人，若x、y满足 ${\begin{matrix} 2 x - y \geq 5 \\ x - y \leq 2 \\ x < 6 \end{matrix}$ ，则该学校今年计划招聘教师最多人．

查看试题解析
16. 四名同学根据各自的样本数据研究变量x，y之间的相关关系，并求得回归直线方程和相关系数r，分别得到以下四个结论：
①y=2.347x﹣6.423，且r=﹣0.9284；
②y=﹣3.476x+5.648，且r=﹣0.9533；
③y=5.437x+8.493，且r=0.9830；
④y=﹣4.326x﹣4.578，且r=0.8997．
其中一定不正确的结论的序号是．

查看试题解析

三、解答题

17. 已知函数f（x）=2 $\sqrt{3}$ sin²（ $\frac{π}{4}$ +x）+2sin（ $\frac{π}{4}$ +x）cos（ $\frac{π}{4}$ +x）．
（Ⅰ）求函数f（x）的单调递增区间及其对称中心；
（Ⅱ）在△ABC中，角A，B，C所对的边分别为a，b，c且角A满足f（A）= $\sqrt{3}$ +1，若a=3，BC边上的中线长为3，求△ABC的面积S．

查看试题解析
18. 某校为了解校园安全教育系列活动的成效，对全校学生进行了一次安全意识测试，根据测试成绩评定“合格”、“不合格”两个等级，同时对相应等级进行量化：“合格”记5分，“不合格”记0分．现随机抽取部分学生的答卷，统计结果及对应的频率分布直方图如图所示：
等级
不合格
合格
得分
[20，40）
[40，60）
[60，80）
[80，100]
频数
6
a
24
b
（Ⅰ）求a，b，c的值；
（Ⅱ）用分层抽样的方法，从评定等级为“合格”和“不合格”的学生中随机抽取10人进行座谈．现再从这10人这任选4人，记所选4人的量化总分为ξ，求ξ的分布列及数学期望E（ξ）；
（Ⅲ）某评估机构以指标M（M= $\frac{E (ξ)}{D (ξ)}$ ，其中D（ξ）表示ξ的方差）来评估该校安全教育活动的成效．若M≥0.7，则认定教育活动是有效的；否则认定教育活动五校，应调整安全教育方案．在（Ⅱ）的条件下，判断该校是否应调整安全教育方案？

查看试题解析
19. 如图，在直角梯形ABCD中AD∥BC．∠ABC=90°，AB=BC=2，DE=4，CE⊥AD于E，把△DEC沿CE折到D′EC的位置，使D′A=2 $\sqrt{3}$ ．
（Ⅰ）求证：BE⊥平面AD′C；
（Ⅱ）求平面D′AB与平面D′CE的所夹的锐二面角的大小．

查看试题解析
20. 已知椭圆 $\frac{x^{2}}{a^{2}}$ + $\frac{y^{2}}{b^{2}}$ =1（a＞b＞0）的焦距为2，且过点（1， $\frac{3}{2}$ ），其长轴的左右两个端点分别为A，B，直线y= $\frac{3}{2}$ x+m交椭圆于两点C，D．

(1)、求椭圆标准的方程；

(2)、设直线AD，CB的斜率分别为k₁ ， k₂ ，若k₁：k₂=2：1，求m的值．

查看试题解析
21. 已知函数f（x）=xlnx，e为自然对数的底数．
（Ⅰ）求曲线y=f（x）在x=e^﹣³处的切线方程；
（Ⅱ）关于x的不等式f（x）≥λ（x﹣1）在（0，+∞）恒成立，求实数λ的取值范围．
（Ⅲ）关于x的方程f（x）=a有两个实根x₁ ， x₂ ，求证：|x₁﹣x₂|＜ $\frac{3}{2}$ a+1+ $\frac{1}{2 e^{3}}$ ．

查看试题解析

等级	不合格		合格
得分	[20，40）	[40，60）	[60，80）	[80，100]
频数	6	a	24	b