2019-2020学年初中数学七年级上学期期末模拟试卷(浙教版)
试卷更新日期:2019-12-20 类型:期末考试
一、单选题
-
1. 下列说法不正确的是:( )
① a一定是正数; ②0的倒数是0 ; ③最大的负整数-1;④只有负数的绝对值是它的相反数; ⑤相反数等于本身的有理数只有0
A、②③④ B、①②④⑤ C、②③④⑤ D、①②④2. 国家体育场“鸟巢”建筑面积达25.8万平方米,将25.8万平方米用科学记数法表示为( )A、25.8×103平方米 B、2.58×103平方米 C、2.58×104平方米 D、2.58×105平方米3. 的平方根是( )A、3 B、±3 C、±9 D、94. 某商品的原价是每件x元,在销售时每件加价20元,再降价15%,则现在每件的售价是( )元.A、15%x+20 B、(1﹣15%)x+20 C、15%(x+20) D、(1﹣15%)(x+20)5. 若 ,则式子 的值为( )
A、-11 B、-1 C、11 D、16. ( )A、1 B、-3 C、3 D、-57. 将一副直角三角尺按如图放置,若∠AOD=20°,则∠BOC的大小是( ) A、110° B、120° C、140° D、160°8. 下列各式变形正确的是( )A、由
A、110° B、120° C、140° D、160°8. 下列各式变形正确的是( )A、由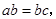 得
B、由
得
B、由 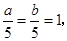 得
得 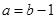 C、由
C、由 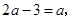 得
D、由 2a-1=3a+1, 得 a=2
9. 已知线段 AB=10cm,直线 AB 上有一点 C,且 BC=4cm,M 是线段 AC 的中点,则 AM 的长( )A、7cm B、3cm C、3cm 或 7cm D、7cm 或 9cm10. 如图所示,某工厂有三个住宅区,A,B,C各区分别住有职工30人,15人,10人,且这三点在一条大道上(A,B,C三点在同一直线上),已知AB=300米,BC=600米.为了方便职工上下班,该厂的接送车打算在此路段只设一个停靠点,为使所有的人步行到停靠点的路程之和最小,那么该停靠点的位置应设在( )
得
D、由 2a-1=3a+1, 得 a=2
9. 已知线段 AB=10cm,直线 AB 上有一点 C,且 BC=4cm,M 是线段 AC 的中点,则 AM 的长( )A、7cm B、3cm C、3cm 或 7cm D、7cm 或 9cm10. 如图所示,某工厂有三个住宅区,A,B,C各区分别住有职工30人,15人,10人,且这三点在一条大道上(A,B,C三点在同一直线上),已知AB=300米,BC=600米.为了方便职工上下班,该厂的接送车打算在此路段只设一个停靠点,为使所有的人步行到停靠点的路程之和最小,那么该停靠点的位置应设在( ) A、点A B、点B C、AB之间 D、BC之间
A、点A B、点B C、AB之间 D、BC之间二、填空题
-
11. 在数轴上到-3的距离为4个单位长度的点表示的数是.12. 若 ,且a,b是两个连续的整数,则a+b的值为13. 单项式 的系数是。14. 已知关于x的一元一次方程 +5=2019x+m的解为x=2018,那么关于y的一元一次方程 ﹣5=2019(5﹣y)﹣m的解为.15. 如图:A地和B地之间途经C、D、E、F四个火车站,且相邻两站之间的距离各不相同,则售票员应准备种火车票.
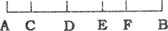 16. 一列匀速行驶的高铁列车在行进途中经过一个长1200米的隧道,已知列车从进入隧道到离开隧道共需8秒时间.出隧道后与另一列长度和速度都相同的列车相遇,从相遇到离开仅用了2秒,则该列车的长度为米.
16. 一列匀速行驶的高铁列车在行进途中经过一个长1200米的隧道,已知列车从进入隧道到离开隧道共需8秒时间.出隧道后与另一列长度和速度都相同的列车相遇,从相遇到离开仅用了2秒,则该列车的长度为米.三、解答题
-
17. 计算:18. 计算:19. 先化简,再求值:[x2y-(1-x2y)]-2(-xy+x2y)-5,其中x=-2,y=1.20. 如图,射线OA、OC在射线OB的异侧且∠BOC = 2∠AOB (∠AOB<60°),射线OD平分∠AOC,请探求∠BOD与∠AOB的数量关系.
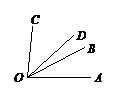
21. 出租车司机小千某天下午营运全是在南北走向的公路上进行的,如果向南记作“+”,向北记作“﹣”,他这天下午行车共6趟,情况记作如下:(单位:千米,每次行车都有乘客)﹣2,+5,﹣2,﹣3,﹣2,+6,请回答:(1)、小王将最后一名乘客送到目的地时,小王在下午出车的出发地的什么方向?跑下午出车的出发地多远?(2)、若小王的出租车每千米耗油0.3升,每升汽油6元,小王这天下午共耗油多少钱?(3)、若规定每趟车的起步价是10元,且每趟车3千米以内(含3千米)只收起步价;若超过3千米,除收起步价外,超过的每千米还需收2元钱,那么小王这天下午收到的乘客所给车费共多少元?那么小王这天下午盈利(或亏损)多少钱?(不计汽车的损耗)22. 甲、乙两工程队承建某校校园绿化工程,已知甲队单独完成需要 9 天,乙队单独 完成需要 18 天.(1)、若先由甲、乙两队合做 4 天,剩下工程由乙队单独完成,则还需几天可完成此项 工程?(2)、在(1)的条件下,工程结束后学校共支付 90 000 元工程款,若按甲、乙两队完成的工作量分配这笔钱,问甲、乙两队各得到多少元工程款?
23. 某超市元月1日搞促销活动,购物不超过200元不给优惠;超过200元,而不超过500元优惠10%;超过500元的,其中500元按9折优惠,超过部分按8折优惠,某人两次购物分别用了134元和466元,问:
(1)、此人两次购物时的物品不打折分别值多少钱?(2)、在这次活动中他节省了多少钱?(3)、若此人将这两次购买的物品合起来一次性购买是不是更合算?说明你的理由。24. 已知数轴上有两点A、B,点A对应的数是40,点B对应的数是﹣80.(1)、求线段AB的长.(2)、如图,O表示原点,动点P、T分别从B、O两点同时出发向左运动,同时动点Q从点A出发向右运动,点P、T、Q的速度分别为5个单位长度/秒、1个单位长度/秒、2个单位长度/秒,设运动时间为t.

①求点P、T、Q表示的数(用含有t的代数式表示);
②在运动过程中,如果点M为线段PT的中点,点N为线段OQ的中点,试说明在运动过程中等量关系PQ+OT=2MN始终成立.