海南省定安县2016-2017学年八年级下学期期末考试数学试题

试卷更新日期：2017-07-27 类型：期末考试

进入出卷网下载

一、选择题。

1. 若分式 $\frac{2}{2 x - 1}$ 有意义，则（）

A、 $x > \frac{1}{2}$ B、 $x \neq \frac{1}{2}$ C、 $x$ ≥ $\frac{1}{2}$ D、 $x = \frac{1}{2}$

查看试题解析
2. 下列约分正确的是（）

A、 $\frac{x^{6}}{x^{2}} = x^{3}$ B、 $\frac{a + c}{b + c} = \frac{a}{b}$ C、 $\frac{a + b}{b + a} = 0$ D、 $\frac{x - y}{y - x} = -1$

查看试题解析
3. 数据1，2，4，4，3的众数是（）

A、1 B、2 C、3 D、4

查看试题解析
4. 点P(-2，5)关于x轴对称的点的坐标为（）

A、(2，-5) B、(5，-2) C、(-2，-5) D、(2，5)

查看试题解析
5. 某校数学兴趣小组12名成员的年龄情况如下：
年龄（岁）
12
13
14
15
16
人数
1
4
3
2
2
则这个小组成员年龄的中位数、平均数分别是（）

A、13、14 B、14、14 C、14、15 D、16、13

查看试题解析
6. 如图，下列四组条件中．不能判定四边形ABCD是平行四边形的是（）

A、AB=DC，AD=BC B、AB∥DC，AD∥BC C、AB∥DC，AD=BC D、AB∥DC，AB=DC

查看试题解析
7. 将直线y=x+1向上平移2个单位，得到直线（）

A、y=x+2 B、y=-x+3 C、y=-x-2 D、y=x+3

查看试题解析
8. 在△ABC中，点E、D、F分别在AB、BC、AC上且DE∥CA，DF∥BA，下列四个判断中不正确的是（）

A、四边形AEDF是平行四边形 B、如果∠BAC=90°，那么四边形AEDF是矩形 C、如果AD⊥BC，那么四边形AEDF是菱形 D、如果AD平分∠BAC，那么四边形AEDF是菱形

查看试题解析
9. 将矩形ABCD沿AE折叠，得到如图所示的图形，已知∠CED′=55°，则∠BAD′的大小是（）

A、30° B、35° C、45° D、60°

查看试题解析
10. 四边形ABCD的对角线相交于点O，能判定它是正方形的条件是（）

A、AB=BC=CD=DA B、AO=CO，BO=DO，AC⊥BD C、AC=BD，AC⊥BD且AC、BD互相平分 D、AB=BC，CD=DA

查看试题解析
11. 已知菱形的两条对角线长分别是6cm和8cm，则菱形的边长是（）

A、12cm B、10cm C、7cm D、5cm

查看试题解析
12. 如果一个四边形的面积正好等于它的两条对角线乘积的一半，那么这个四边形一定是（）

A、菱形 B、矩形 C、正方形 D、对角线互相垂直的四边形

查看试题解析
13. 如图，在正方形ABCD内部作等边三角形BCE，则∠AEB的度数为（）

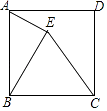A、60° B、65° C、70° D、75°

查看试题解析
14.
如图，一次函数与反比例函数的图象交于A、B两点，则图中使反比例函数小于一次函数的自变量x的取值范围是（）

A、x＜-1 B、x＞ 2 C、-1＜x＜0或x＞2 D、x＜-1或0＜x＜2

查看试题解析

二、填空题

15. 计算： $2^{- 2} \times {(\frac{1}{2017})}^{0} =$ ．

查看试题解析
16. 方程 $\frac{1}{x} - \frac{2}{2 - x} = 0$ 的解是．

查看试题解析
17.
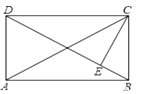
已知：如图，在矩形ABCD中，CE⊥BD，E为垂足，∠DCE：∠ECB=3：1，则∠ACE=.

查看试题解析
18.
已知，如图，在平面直角坐标系中，O为坐标原点，四边形OABC是矩形，点A、C的坐标分别为A（10，0）、C（0，4），点D是OA的中点，点P在BC边上运动，△ODP是腰长为5的等腰三角形时，点P的坐标为.

查看试题解析

三、解答题

19. 综合题。

(1)、计算： $2^{2} + {(- \frac{1}{2})}^{- 2} - 3^{- 1} + \sqrt{\frac{1}{9}} + {(π - 3.14)}^{0}$

(2)、解方程： $\frac{3}{x - 2} = 2 + \frac{x}{2 - x}$

查看试题解析
20. 列分式方程解应用题：今年植树节，某校师生到距学校20千米的公路旁植树，一班师生骑自行车先走，走了16千米后，二班师生乘汽车出发，结果同时到达．已知汽车的速度比自行车的速度每小时快60千米，求两种车的速度各是多少？

查看试题解析
21. 先化简，再求值： $(\frac{3 a}{a - 1} - \frac{a}{a + 1}) \cdot \frac{a^{2} - 1}{a}$ ，其中 $a = 2$ ．

查看试题解析
22.
如图，四边形ABCD为正方形．点A的坐标为（0，2），点B的坐标为（0，﹣3），反比例函数 $y = \frac{k}{x}$ 的图象经过点C，一次函数y=ax+b的图象经过点A、C，

(1)、求反比例函数与一次函数的解析式；

(2)、若点P是反比例函数图象上的一点，△OAP的面积恰好等于正方形ABCD的面积，求P点的坐标．

查看试题解析
23.
如图，已知△ABC中，D是BC边上的一点，E是AD的中点，过A点作BC的平行线，交CE的延长线于点F，且AF=BD，连接BF．

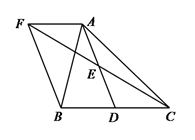(1)、求证：BD=CD；

(2)、如果AB=AC，试判断四边形AFBD的形状，并证明你的结论．

查看试题解析
24.
综合题。

(1)、如图（1）点P是正方形ABCD的边CD上一点（点P与点C，D不重合），点E在BC的延长线上，且CE=CP，连接BP，DE．求证：BP=DE且BP⊥DE；

(2)、直线EP交AD于F，连接BF，FC．点G是FC与BP的交点．
①若BC=2CE时，求证：BP⊥CF；
②若BC=n•CE（n是大于1的实数）时，记△BPF的面积为S₁ ， △DPE的面积为S₂ ．
求证：S₁=（n+1）S₂ ．

查看试题解析

年龄（岁）	12	13	14	15	16
人数	1	4	3	2	2