北京市通州区2016-2017学年八年级下学期期末考试数学试题
试卷更新日期:2017-07-27 类型:期末考试
一、选择题。
-
1. 一元二次方程 的二次项系数、一次项系数及常数项分别是( )A、 , , B、 , , C、 , , D、 , ,2. 我国传统文化中的“福禄寿喜”图由下面四个图案构成.这四个图案中既是轴对称图形,又是中心对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 3.
3.如图,在菱形 中,对角线 、 交于点 .若 , ,则 的长为( )
 A、1 B、 C、2 D、4. 某洗衣机在洗涤衣服时经历了注水、清洗、排水三个连续过程(工作前洗衣机内无水),在这三个过程中洗衣机内水量y(升)与时间x(分)之间的函数关系对应的图象大致为( )A、
A、1 B、 C、2 D、4. 某洗衣机在洗涤衣服时经历了注水、清洗、排水三个连续过程(工作前洗衣机内无水),在这三个过程中洗衣机内水量y(升)与时间x(分)之间的函数关系对应的图象大致为( )A、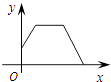 B、
B、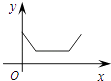 C、
C、 D、
D、 5. 很多运动员为了参加北京—张家口冬季奥运会,进行了积极的训练.下表记录了国家队4名队员在500米短道速滑训练成绩的平均数 与方差 :
5. 很多运动员为了参加北京—张家口冬季奥运会,进行了积极的训练.下表记录了国家队4名队员在500米短道速滑训练成绩的平均数 与方差 :队员甲
队员乙
队员丙
队员丁
平均数 (秒)
45
46
45
46
方差 (秒2)
1.5
1.5
3.5
4.5
根据表中数据,要从中选择一名成绩好又发挥稳定的运动员参加比赛,应该选择( )
A、队员甲 B、队员乙 C、队员丙 D、队员丁6. 若一次函数 的函数值 随 的增大而减小,且图象与 轴的负半轴相交,那么对 和 的符号判断正确的是( )A、 , B、 , C、 , D、 ,7. 若关于x的一元二次方程 有两个不相等的实数根,则k的取值范围是( )A、k > 1 B、 C、k < 1 D、k < 1且8.如图所示,在一幅长 ,宽 的矩形风景画的四周镶一条金色纸边,制成一幅矩形挂图.如果要使整幅挂图的面积是 ,设金色纸边的宽为 ,那么 满足的方程是( )
 A、 B、 C、 D、9.
A、 B、 C、 D、9.如图所示,在矩形纸片 中, , 为 边上两点,且 ; , 为 边上两点,且 .沿虚线 折叠,使点 落在点 上,点 落在点 上;然后再沿虚线 折叠,使 落在点 上,点 落在点 上.叠完后,剪一个直径在 上的半圆,再展开,则展开后的图形为( )
 A、
A、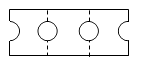 B、
B、 C、
C、 D、
D、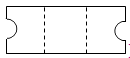 10.
10.如图,在平面直角坐标系 中, , ,一次函数 与线段 有公共点,则 的取值范围是( )
 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
11. 在平面直角坐标系中,点 的坐标为 ,则点 关于 轴的对称点的坐标是 .12.
一次函数 的图象如图所示,其中b = , k = .
 13. 如果 是一元二次方程 的一个解,那么代数式 的值为 .14.
13. 如果 是一元二次方程 的一个解,那么代数式 的值为 .14.线段 是由线段 平移得到的,点 的对应点为 ,则点 的对应点 的坐标是 .
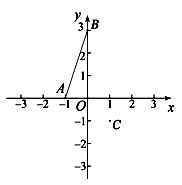 15.
15.如图,点 是矩形 的对角线 的中点, 是 边的中点.若 , ,则线段 的长为 .
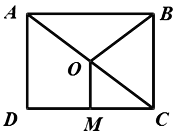 16.
16.阅读下面材料:
在数学课上,老师提出如下问题:

小颖的作法如下:
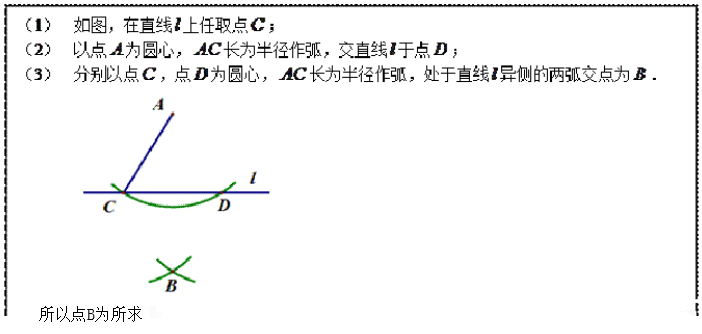
老师说:“小颖的作法正确.”
请回答:小颖的作图依据是.17. 解下列一元二次方程:(1)、
(2)、
18. 在平面直角坐标系 中,已知一次函数 与 相交于点 ,且 与 轴交于点 .(1)、求一次函数 和 的解析式;(2)、当 时,求出 的取值范围.
19.已知:如图, , , , 在同一直线上,且 , , .求证:四边形 是平行四边形.
 20. 已知关于 的一元二次方程 有两个不相等的实数根(1)、求 的取值范围;(2)、若 为正整数,且该方程的根都是整数,求 的值。21. 生产某电器,原来每件的成本是300元,由于技术革新,连续两次降低成本,现在的成本是192元。每次降低成本时,成本的平均降低率是多少?22. 下表是初二年级50名同龄女生身高数据:
20. 已知关于 的一元二次方程 有两个不相等的实数根(1)、求 的取值范围;(2)、若 为正整数,且该方程的根都是整数,求 的值。21. 生产某电器,原来每件的成本是300元,由于技术革新,连续两次降低成本,现在的成本是192元。每次降低成本时,成本的平均降低率是多少?22. 下表是初二年级50名同龄女生身高数据:身高/cm
146
151
153
154
156
157
158
159
160
人数
1
2
2
2
3
4
8
4
4
身高/cm
161
162
163
164
165
166
167
169
人数
2
4
3
2
3
4
1
1
(1)、根据下表的分组方法进行数据整理,补全频数分布表:
 (2)、根据分布表画出频数分布直方图.
(2)、根据分布表画出频数分布直方图.
(3)、观察频数分布表和频数分布直方图回答问题:为了参加广播操比赛,老师打算从以上50名女生中挑选30名队员。为了让参赛队员的身高比较整齐,老师应该选择身高在什么范围内的同学呢?请写出答案并简述理由.
23. 阅读下面材料:学习了《平行四边形》单元知识后,小东根据学习平行四边形的经验,对矩形的判定问题进行了再次探究.以下是小东的探究过程,请你补充完整:
(1)、在平行四边形ABCD中,对角线AC与BD相交于点O . 补充下列条件中能判断平行四边形ABCD是矩形的是 (请将所有正确答案前的字母填写在横线上)A、AC⊥BD B、 AC=BD C、 AD=DC D、∠DAB=∠ABC(2)、小东进一步探究发现:在通过对“边、角、对角线”研究矩形的判定中,小东提出了一个猜想:“一组对边相等,一组对角均为直角的四边形为矩形.” 请你画出图形,判断小东的猜想是否是证明题.如果是真命题,请写出证明过程,如果不是,请说明理由.
24.如图,在平行四边形 中,点 是 边上任意一点,连接 .过点 作线段 的平行线,交 延长线于点 .
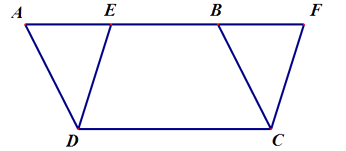 (1)、证明: .(2)、过点 作 ,垂足为点 .点 为 边中点,连接 , .
(1)、证明: .(2)、过点 作 ,垂足为点 .点 为 边中点,连接 , .① 根据题意完成作图;
② 猜想线段 , 的数量关系,并写出你的证明思路.
25.我们对平面直角坐标系 中的三角形给出新的定义:三角形的“横长”和三角形的“纵长”.我们假设点 , 是三角形边上的任意两点.如果 的最大值为 ,那么三角形的“横长” ;如果 的最大值为 ,那么三角形的“纵长” .如右图,该三角形的“横长” ;“纵长” .
当 时,我们管这样的三角形叫做“方三角形”.
 (1)、
(1)、如图1所示,

已知点 , .
在点 , , 中,可以和点 ,点 构成“方三角形”的点是;
(2)、若点 在函数 上,且 为“方三角形”,求点 的坐标;(3)、如图2所示,已知点 , ,点 为平面直角坐标系中任意一点.若 为“方三角形”,且 ,请直接写出点 的坐标.
