北京市石景山区2016-2017学年八年级下学期期末考试数学试题

试卷更新日期：2017-07-27 类型：期末考试

进入出卷网下载

一、选择题

1. 在平面直角坐标系中,点 $M (- 1$ ， $5 ）$ 所在的象限是（）

A、第一象限 B、第二象限 C、第三象限 D、第四象限

查看试题解析
2.
剪纸是中国古老的汉族传统民间艺术之一.下面
是制作剪纸的简单流程，展开后的剪纸图案从对称性来判断（）

A、是轴对称图形但不是中心对称图形 B、是中心对称图形但不是轴对称图形 C、既是轴对称图形也是中心对称图形 D、既不是轴对称图形也不是中心对称图形

查看试题解析
3. 如果一个n边形的内角和与外角和相等，那么这个n边形是（）

A、四边形 B、五边形 C、六边形 D、七边形

查看试题解析
4.
如图，在□ $A B C D$ 中， $E$ 是 $B C$ 边的中点， $F$ 是对角线 $A C$ 的中点，若 $E F = 5$ ，则 $D C$ 的长为（）

A、2.5 B、5 C、10 D、15

查看试题解析
5. 在下列图形性质中，平行四边形不一定具备的是（）

A、对角线相等 B、两组对边分别平行 C、两组对边分别相等 D、对角线互相平分

查看试题解析
6. 下表记录了甲、乙、丙、丁四名跳高运动员最近几次选拔赛成绩的平均数与方差：

甲
乙
丙
丁
平均数（cm）
182
182
182
182
方差
5.7
3.5
7.1
8.6

要从中选择一名发挥稳定的运动员去参加比赛，应该选择（）

A、甲 B、乙 C、丙 D、丁

查看试题解析
7. 关于 $x$ 的一次函数 $y = k x + k^{2} + 1$ 的图象可能是（）

A、 B、 C、 D、

查看试题解析
8. 关于x的一元二次方程 $m x^{2} + 2 x - 1 = 0$ 有两个实数根，则m的取值范围是（）

A、 $m \leq - 1$ B、 $m \geq - 1$ C、 $m \leq 1$ 且 $m \neq 0$ D、 $m \geq - 1$ 且 $m \neq 0$

查看试题解析
9. 一列快车以100千米/小时的速度从甲地驶往乙地，一列特快车以150千米/小时的速度从乙地驶往甲地，甲、乙两地之间的距离为1000千米．两车同时出发，则大致表示两车之间的距离y（千米）与快车行驶时间t（小时）之间的函数图象是（）

A、 B、 C、 D、

查看试题解析
10. 把直线 $y = - 5 x + 3$ 向上平移 $m$ 个单位后，与直线 $y = 2 x + 4$ 的交点在第一象限，则 $m$ 的取值范围是（）

A、 $m < 4$ B、 $m > 1$ C、 $1 < m < 7$ D、 $3 < m < 4$

查看试题解析

二、填空题

11. 点P（－3，2）到 $x$ 轴的距离是

查看试题解析
12. 请写出一个图象过点 $(0, 1)$ ，且函数值 $y$ 随自变量 $x$ 的增大而减小的一次函数的表达式：（填上一个答案即可）．

查看试题解析
13. 已知一次函数 $y = k x + 2 (k \neq 0)$ 与 $x$ 轴， $y$ 轴分别交于点 $A$ ，点 $B$ ，若 $O B = 2 O A$ ，则 $k$ 的值是

查看试题解析
14.
如图1，将正方形 $A B C D$ 置于平面直角坐标系中，其中 $A D$ 边在 $x$ 轴上，其余各边均与坐标轴平行.直线 $l ： y = x - 3$ 沿 $x$ 轴的负方向以每秒1个单位的速度平移，在平移的过程中，该直线被正方形 $A B C D$ 的边所截得的线段长为 $m$ ，平移的时间为 $t$ （秒）， $m$ 与 $t$ 的函数图象如图2所示，则图1中的点 $A$ 的坐标为，图2中 $b$ 的值为.
图1 图2

查看试题解析
15.
已知：线段 $A B$ ， $B C$ ， $∠ A B C = 90 °$ . 求作：矩形 $A B C D$ .
以下是甲、乙两同学的作业：
甲：① 以点 $C$ 为圆心， $A B$ 长为半径作弧；
② 以点 $A$ 为圆心， $B C$ 长为半径作弧；
③ 两弧在 $B C$ 上方交于点 $D$ ，连接 $A D$ ， $C D$ .
四边形 $A B C D$ 即为所求矩形.（如图）
乙：① 连接 $A C$ ，作线段 $A C$ 的垂直平分线，交 $A C$ 于点 $M$ ；
② 连接 $B M$ 并延长，在延长线上取一点 $D$ ，使 $M D = M B$ ，连接 $A D$ ， $C D$ .
四边形 $A B C D$ 即为所求矩形.（如图）
老师说甲、乙同学的作图都正确.
则甲的作图依据是：；
乙的作图依据是：.

查看试题解析

三、解答题

16. 用适当的方法解方程： $x^{2} + 4 x - 1 = 0$

查看试题解析
17.
如图，矩形 $A B C D$ ， $E$ 为射线 $C D$ 上一点，连接 $A E$ ， $F$ 为 $A E$ 上一点， $F C$ 交 $A D$ 于点 $G$ ， $F A = F G$ ．
求证： $F E = F C$ ．

查看试题解析
18.
如图，在□ $A B C D$ 中，过点 $A$ 作 $A E$ ⊥ $B C$ 于点 $E$ ， $A F$ ⊥ $D C$ 于点 $F$ ， $A E = A F$ ．
求证：四边形 $A B C D$ 是菱形．

查看试题解析
19. 已知关于 $x$ 的方程 $m x^{2} + (2 m - 1) x + m - 1 = 0 （ m \neq 0 ）$ .

(1)、求证：方程总有两个不相等的实数根；

(2)、若方程的两个实数根都是整数，求整数 $m$ 的值.

查看试题解析
20.
如图，四边形ABCD为平行四边形，∠BAD的角平分线AF交CD于点E ，交BC的延长线于点F ．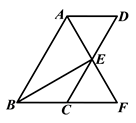

(1)、求证：BF=CD；

(2)、连接BE ，若BE⊥AF ， ∠F=60°， $B E = 2 \sqrt{3}$ ，求 $A B$ 的长．

查看试题解析
21. 列方程或方程组解应用题：某项工程，甲队单独完成所需时间比乙队单独完成所需的时间多5个月，并且两队单独完成所需时间的乘积恰好等于两队单独完成所需时间之和的6倍．求甲、乙两队单独完成这项工程各需几个月?

查看试题解析
22.
为进一步加强中小学生近视眼的防控工作，某地区教育主管部门对初二年级学生的视力进行了一次抽样调查，经数据分组整理，绘制的频数分布表与频数分布直方图的一部分如下（每组含前一个边界值，不含后一个边界值）：
请根据以上信息解答下列问题：

(1)、表中的 $a =$ ， $b =$ ；

(2)、在图中补全频数分布直方图；

(3)、若视力在 $5.0$ 以上（含 $5.0$ ）均属正常，根据抽样调查数据，估计该地区6200名初二年级学生视力正常的有人.

查看试题解析
23.
一个装有进水管和出水管的容器，从某时刻开始的4分钟内只进水不出水，在随后的8分钟内既进水又出水，接着关闭进水管直到容器内的水放完．假设每分钟的进水量和出水量是两个常数，容器内的水量y（单位：升）与时间x（单位：分钟）之间的部分关系如图象所示．求从关闭进水管起需要多少分钟该容器内的水恰好放完．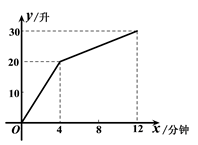

查看试题解析
24.
如图，在平面直角坐标系 $x O y$ 中，直线 $l_{1} ： y = m x (m \neq 0)$ 与直线 $l_{2} ： y = a x + b (a \neq 0)$ 相交于点A（2，4），直线 $l_{2}$ 与x轴交于点B（6，0）．

(1)、分别求直线 $l_{1}$ 和 $l_{2}$ 的表达式；

(2)、过动点P（0，n）且垂直于 $y$ 轴的直线与 $l_{1}$ ， $l_{2}$ 的交点分别为C ， D ，当点C 位于点D左方时，请直接写出n的取值范围．

查看试题解析
25.
在矩形 $A B C D$ 中， $A D = 12$ ， $D C = 8$ ，点 $F$ 是 $A D$ 边上一点，过点 $F$ 作 $∠ A F E = ∠ D F C$ ，交射线 $A B$ 于点 $E$ ，交射线 $C B$ 于点 $G$ ．

(1)、如图1，若 $F G = 8 \sqrt{2}$ ，则 $∠ C F G =$ 度；

(2)、当以 $F$ ， $G$ ， $C$ 为顶点的三角形是等边三角形时，依题意在图2中补全图形并求 $B G$ 的长；

(3)、过点 $E$ 作 $E H$ ∥ $C F$ 交射线 $C B$ 于点 $H$ ，请探究：当 $B G$ 为何值时，以 $F$ ， $H$ ， $E$ ， $C$ 为顶点的四边形是平行四边形．

查看试题解析

	甲	乙	丙	丁
平均数（cm）	182	182	182	182
方差	5.7	3.5	7.1	8.6