北京市房山区2016-2017学年八年级下学期期末考试数学试题
试卷更新日期:2017-07-27 类型:期末考试
一、选择题
-
1. 点 所在象限是( )A、第一象限 B、第二象限 C、第三象限 D、第四象限2. 下列剪纸作品中,是中心对称图形的为( ).A、
 B、
B、 C、
C、 D、
D、 3. 某多边形的每个内角均为120°,则此多边形的边数为( ).A、5 B、6 C、7 D、84. 下列各点中,在一次函数 的图象上的点为( ).A、(3,5) B、(2,-2) C、(2,7) D、(4,9)5.
3. 某多边形的每个内角均为120°,则此多边形的边数为( ).A、5 B、6 C、7 D、84. 下列各点中,在一次函数 的图象上的点为( ).A、(3,5) B、(2,-2) C、(2,7) D、(4,9)5.如图,在▱ABCD中,AB=4,AD=7,∠ABC的平分线BE交AD于点E , 则DE的长是( )
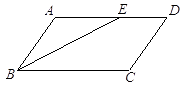 A、4 B、3 C、3.5 D、26. 方程 的根的情况是( ).A、有两个不相等的实数根 B、有两个相等的实数根 C、有一个实数根 D、没有实数根7. 用配方法解方程 ,方程应变形为( ).
A、4 B、3 C、3.5 D、26. 方程 的根的情况是( ).A、有两个不相等的实数根 B、有两个相等的实数根 C、有一个实数根 D、没有实数根7. 用配方法解方程 ,方程应变形为( ).
A、 B、 C、 D、8.已知关于x的方程
 有两个实数根,则m的取值范围是( ).A、 B、 C、 D、9.
有两个实数根,则m的取值范围是( ).A、 B、 C、 D、9.如图,在△ABC中,AB=6,AC=10,点D , E , F分别是AB , BC , AC的中点,则四边形ADEF的周长为( ).
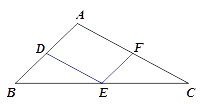 A、16 B、12 C、10 D、810. 2022年将在北京---张家口举办冬季奥运会,很多学校开设了相关的课程.某校8名同学参加了滑雪选修课,他们被分成甲、乙两组进行训练,身高(单位:cm)如下表所示:
A、16 B、12 C、10 D、810. 2022年将在北京---张家口举办冬季奥运会,很多学校开设了相关的课程.某校8名同学参加了滑雪选修课,他们被分成甲、乙两组进行训练,身高(单位:cm)如下表所示:队员1
队员2
队员3
队员4
甲组
176
177
175
176
乙组
178
175
177
174
设两队队员身高的平均数依次为 , ,方差依次为 , ,则下列关系中完全正确的是( )
A、 B、 C、 D、二、填空题.
-
11. 已知正方形的一条边长为2,则它的对角线长为12.
如图,是利用平面直角坐标系画出的天安门广场的平面示意图,若这个坐标系分别以正东、 正北方向为x轴、y轴的正方向, 表示毛主席纪念堂的点的坐标为(0,-3), 表示中国国家博物馆的点的坐标为(4,1), 则表示人民大会堂的点的坐标为;
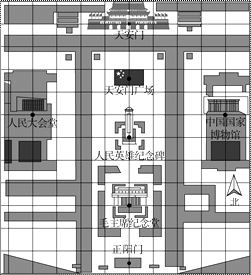 13.
13.有两名学员小林和小明练习射击,第一轮10枪打完后两人打靶的环数如图所示,已知新手的成绩不太稳定,那么根据图中的信息,估计小林和小明两人中新手是 .
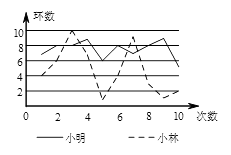 14.
14.如图,在平面直角坐标系xOy中,A(1,1),B(2,2),直线 与线段AB有公共点,则 的取值范围是 .
 15.
15.如图,菱形ABCD的周长为16,若 ,E是AB的中点,则点E的坐标为 .
三、解答题。
-
16.
阅读下面材料:
在数学课上,老师提出如下问题:
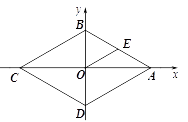
已知:如图,四边形ABCD是平行四边形
求作:菱形AECF,使E,F分别在BC,AAD上

小凯的作法如下:
⑴连接AC
⑵作AC的垂直平分线EF分别交BC,AD于E,F
⑶连接AE,CF
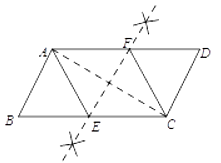
所以四边形AECF是菱形
老师说:“小凯的作法正确.”
请回答:在小凯的作法中,判定四边形AECF是菱形的依据是
四、解答题
-
17. 解方程: .18. 已知一次函数 中,y随x的增大而减小,且其图象与y轴交点在x轴上方.求m的取值范围.19.
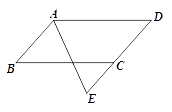
如图,四边形ABCD是平行四边形,AE平分∠BAD , 交DC的延长线于点E.求证:BC=DE
 20.
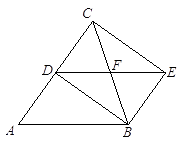
20.如图,在△ABC中,AB=BC , BD平分∠ABC . 过点D作AB的平行线,过点B作AC的平行线,两平行线相交于点E , BC交DE于点F , 连接CE . 求证:四边形BECD是矩形.
 21.
21.已知一次函数 的图象经过点A(2,0),与y轴交于点B(0,4).
 (1)、求一次函数的表达式;并在平面直角坐标系内画出该函数的图象;(2)、当自变量x=-5时,求函数y的值;(3)、当x>0时,请结合图象,直接写出y的取值范围.22.
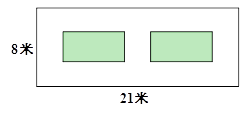
(1)、求一次函数的表达式;并在平面直角坐标系内画出该函数的图象;(2)、当自变量x=-5时,求函数y的值;(3)、当x>0时,请结合图象,直接写出y的取值范围.22.某小区有一块长21米,宽8米的矩形空地,如图所示.社区计划在其中修建两块完全相同的矩形绿地,并且两块绿地之间及四周都留有宽度为x米的人行通道.如果这两块绿地的面积之和为60平方米,人行通道的宽度应是多少米?
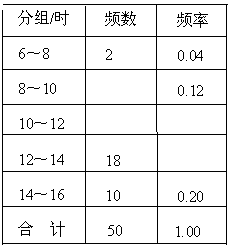
 23. 已知关于x的方程 有两个不相等的实数根.(1)、求m的取值范围;(2)、当m为正整数时,求方程的根.24. 某课外小组为了解本校2014-2015学年八年级700名学生每学期参加社会实践活动的时间,随机对该年级50名学生进行了调查,根据收集的数据绘制了如下的频数分布表和频数分布直方图(各组数据包括最小值,不包括最大值).(1)、
23. 已知关于x的方程 有两个不相等的实数根.(1)、求m的取值范围;(2)、当m为正整数时,求方程的根.24. 某课外小组为了解本校2014-2015学年八年级700名学生每学期参加社会实践活动的时间,随机对该年级50名学生进行了调查,根据收集的数据绘制了如下的频数分布表和频数分布直方图(各组数据包括最小值,不包括最大值).(1)、补全下面的频数分布表和频数分布直方图:
 (2)、可以估计这所学校2014-2015学年八年级的学生中,每学期参加社会实践活动的时间不少于8小时的学生大约有多少人?25.
(2)、可以估计这所学校2014-2015学年八年级的学生中,每学期参加社会实践活动的时间不少于8小时的学生大约有多少人?25.如图所示,在长方形ABCD中,AB=8,BC=4,将长方形沿AC折叠,使点D落在点D′处,求重叠部分△AFC的面积.
 26.
26.在平面直角坐标系xOy中,对于点P(x , y)和Q(x , y′),给出如下定义:若 ,则称点Q为点P的“可控变点”.例如:点(1,2)的“可控变点”为点(1,2).
结合定义,请回答下列问题:
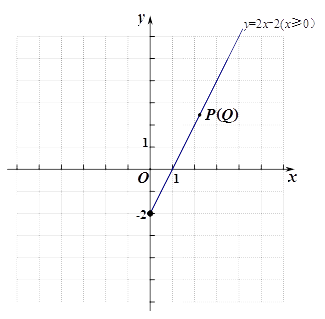 (1)、点(-3,4)的“可控变点”为点 .(2)、若点N(m,2)是函数 图象上点M的“可控变点”,则点M的坐标为;(3)、点P为直线 上的动点,当x≥0时,它的“可控变点”Q所形成的图象如下图所示(实线部分含实心点).请补全当x<0时,点P的“可控变点” Q所形成的图象;
(1)、点(-3,4)的“可控变点”为点 .(2)、若点N(m,2)是函数 图象上点M的“可控变点”,则点M的坐标为;(3)、点P为直线 上的动点,当x≥0时,它的“可控变点”Q所形成的图象如下图所示(实线部分含实心点).请补全当x<0时,点P的“可控变点” Q所形成的图象;
-