北京市西城区2016-2017学年八年级下学期期末考试数学试题
试卷更新日期:2017-07-27 类型:期末考试
一、选择题
-
1. 函数 中,自变量x的取值范围是( ).A、x≠ B、x≠1 C、x> D、x≥2. 一次函数 的图象不经过的象限是( ).A、第一象限 B、第二象限 C、第三象限 D、第四象限3. 彩陶、玉器、青铜器等器物以及壁画、织锦上美轮美奂的纹样,穿越时空,向人们呈现出古代中国丰富多彩的物质与精神世界,各种纹样经常通过平移、旋转、轴对称以及其它几何构架连接在一起,形成复杂而精美的图案.以下图案纹样中,从整体观察(个别细微之处的细节忽略不计),大致运用了旋转进行构图的是( )
A、 B、
B、 C、
C、 D、
D、 4.
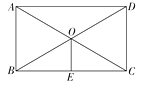
4.如图,矩形ABCD的对角线AC , BD的交点为O , 点E为BC边的中点, ,如果OE=2,那么对角线BD的长为( ).
 A、4 B、6 C、8 D、105. 如果关于x的方程 有两个相等的实数根,那么以下结论正确的是( ).A、 B、 C、k> D、k>16. 下列命题中,不正确的是( ).A、平行四边形的对角线互相平分 B、矩形的对角线互相垂直且平分 C、菱形的对角线互相垂直且平分 D、正方形的对角线相等且互相垂直平分7. 北京市6月某日10个区县的最高气温如下表:(单位:℃)
A、4 B、6 C、8 D、105. 如果关于x的方程 有两个相等的实数根,那么以下结论正确的是( ).A、 B、 C、k> D、k>16. 下列命题中,不正确的是( ).A、平行四边形的对角线互相平分 B、矩形的对角线互相垂直且平分 C、菱形的对角线互相垂直且平分 D、正方形的对角线相等且互相垂直平分7. 北京市6月某日10个区县的最高气温如下表:(单位:℃)区县
大兴
通州
平谷
顺义
怀柔
门头沟
延庆
昌平
密云
房山
最高气温
32
32
30
32
30
32
29
32
30
32
则这10个区县该日最高气温的中位数是( ).
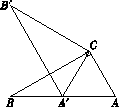
A、32 B、31 C、30 D、298.如图,在Rt△ABC中,∠ACB =90°,∠ABC=30°,将△ABC绕点C顺时针旋转 角(0°< <180°)至△A′B′C , 使得点A′恰好落在AB边上,则 等于( ).
 A、150° B、90° C、60° D、30°9. 教育部发布的统计数据显示,近年来越来越多的出国留学人员学成后选择回国发展,留学回国与出国留学人数“逆差”逐渐缩小.2014年各类留学回国人员总数为36.48万人,而2016年各类留学回国人员总数为43.25万人.如果设2014年到2016年各类留学回国人员总数的年平均增长率为x , 那么根据题意可列出关于x的方程为( ).A、 B、 C、 D、10.
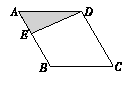
A、150° B、90° C、60° D、30°9. 教育部发布的统计数据显示,近年来越来越多的出国留学人员学成后选择回国发展,留学回国与出国留学人数“逆差”逐渐缩小.2014年各类留学回国人员总数为36.48万人,而2016年各类留学回国人员总数为43.25万人.如果设2014年到2016年各类留学回国人员总数的年平均增长率为x , 那么根据题意可列出关于x的方程为( ).A、 B、 C、 D、10.如图,点E为菱形ABCD边上的一个动点,并沿ABCD的路径移动,设点E经过的路径长为x , △ADE的面积为y , 则下列图象能大致反映y与x的函数关系的是( ).
 A、
A、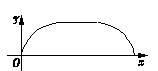 B、
B、 C、
C、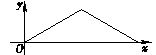 D、
D、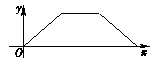
二、填空题
-
11. 如果关于x的方程 有两个相等的实数根,那么m的值为 .12. 如果平行四边形的一条边长为4cm,这条边上的高为3cm,那么这个平行四边形的面积等于13. 在平面直角坐标系xOy中,直线 与x轴的交点坐标为 , 与y轴的交点坐标为 , 与坐标轴所围成的三角形的面积等于.14.
如图,在 ABCD中,CH⊥AD于点H , CH与BD的交点为E.如果 , ,那么
 15.
15.如图,函数 与函数 的图象交于点P , 那么点P的坐标为 , 关于x的不等式 的解集是 .
 16. 写出一个一次函数的解析式,满足以下两个条件:①y随x的增大而增大;②它的图象经过 坐标为 的点. 你写出的解析式为.17.
16. 写出一个一次函数的解析式,满足以下两个条件:①y随x的增大而增大;②它的图象经过 坐标为 的点. 你写出的解析式为.17.如图,正方形ABCD的边长为2cm,正方形AEFG的边长为1cm. 正方形AEFG绕点A旋转的过程中,线段CF的长的最小值为cm.

三、解答题
-
18.
利用勾股定理可以在数轴上画出表示 的点,请依据以下思路完成画图,并保留画图痕迹:
 (1)、第一步:(计算)尝试满足 ,使其中a , b都为正整数.你取的正整数a= , b=;(2)、第二步:(画长为 的线段)以第一步中你所取的正整数a , b为两条直角边长画Rt△OEF , 使O为原点,点E落在数轴的正半轴上, ,则斜边OF的长即为 .请在下面的数轴上画图:(第二步不要求尺规作图,不要求写画法)(3)、第三步:(画表示 的点)在下面的数轴上画出表示 的点M , 并描述第三步的画图步骤:19. 解方程: .20.
(1)、第一步:(计算)尝试满足 ,使其中a , b都为正整数.你取的正整数a= , b=;(2)、第二步:(画长为 的线段)以第一步中你所取的正整数a , b为两条直角边长画Rt△OEF , 使O为原点,点E落在数轴的正半轴上, ,则斜边OF的长即为 .请在下面的数轴上画图:(第二步不要求尺规作图,不要求写画法)(3)、第三步:(画表示 的点)在下面的数轴上画出表示 的点M , 并描述第三步的画图步骤:19. 解方程: .20.如图,在四边形ABCD中,AD//BC , AB=10,BC=6,AC=AD=8.
 (1)、求∠ACB的度数;(2)、求CD边的长.21.
(1)、求∠ACB的度数;(2)、求CD边的长.21.《九章算术》卷九“勾股”中记载:今有户不知高广,竿不知长短.横之不出四尺,纵之不出二尺,斜之适出注.问户斜几何.
注释:横放,竿比门宽长出四尺;竖放,竿比门高长出二尺;斜放恰 好能出去.解决下列问题:
 (1)、示意图中,线段CE的长为尺,线段DF的长为尺;(2)、求户斜多长.22. 2016年9月开始,初二年级的同学们陆续到北京农业职业技术学院进行了为期一周的学农教育活动.丰富的课程开阔了同学们的视野,其中“酸奶的制作”课程深受同学们喜爱.学农1班和学农2班的同学们经历“煮奶—降温—发酵—后熟”四步,制作了“凝固型”酸奶.现每班随机抽取10杯酸奶做样本(每杯100克),记录制作时所添加蔗糖克数如表1、表2所示.
(1)、示意图中,线段CE的长为尺,线段DF的长为尺;(2)、求户斜多长.22. 2016年9月开始,初二年级的同学们陆续到北京农业职业技术学院进行了为期一周的学农教育活动.丰富的课程开阔了同学们的视野,其中“酸奶的制作”课程深受同学们喜爱.学农1班和学农2班的同学们经历“煮奶—降温—发酵—后熟”四步,制作了“凝固型”酸奶.现每班随机抽取10杯酸奶做样本(每杯100克),记录制作时所添加蔗糖克数如表1、表2所示.表1 学农1班所抽取酸奶添加蔗糖克数统计表 (单位:克)
编号
1
2
3
4
5
6
7
8
9
10
蔗糖质量
4.5
5.8
5.4
6.9
4.2
7
4.9
5.8
9.8
6.8
表2,学农2班所抽取酸奶添加蔗糖克数统计表(单位:克)
编号
1
2
3
4
5
6
7
8
9
10
蔗糖质量
7.4
4.9
7.8
4.1
7.2
5.8
7.6
6.8
4.5
4.9
据研究发现,若蔗糖含量在5%~8%,即100克酸奶中,含糖5~8克的酸奶口感最佳.两班所抽取酸奶的相关统计数据如表3所示.
表3两班所抽取酸奶的统计数据表
酸奶口感最佳的杯数
(杯)
每杯酸奶中添加的
蔗糖克数平均值(克)
每杯酸奶中添加的
蔗糖克数的方差
学农1班
x
6.11
2.39
学农2班
6
6.1
1.81
根据以上材料回答问题:
(1)、表3中,x=:(2)、根据以上信息,你认为哪个学农班的同学制作的酸奶整体口感较优?请说明理由.23. 综合题。(1)、阅读以下内容并回答问题:

小雯用这个方法进行了尝试,点 向上平移3个单位后的对应点 的坐标为 , 过点 的直线的解析式为.
(2)、小雯自己又提出了一个新问题请全班同学一起解答和检验此方法,请你也试试看:将直线 向右平移1个单位,平移后直线的解析式为 , 另外直接将直线 向(填“上”或“下”)平移个单位也能得到这条直线.
(3)、请你继续利用这个方法解决问题:
对于平面直角坐标系xOy内的图形M,将图形M上所有点都向上平移3个单位,再向右平移1个单位,我们把这个过程称为图形M的一次“斜平移”. 求将直线 进行两次“斜平移”后得到的直线的解析式.
 24.
24.如下图。
 (1)、画图-连线-写依据:
(1)、画图-连线-写依据:先分别完成以下画图(不要求尺规作图),再与判断四边形DEMN形状的相应结论连线,并写出判定依据(只将最后一步判定特殊平行四边形的依据填在横线上).
①如图1,在矩形ABEN中,D为对角线的交点,过点N画直线NP∥DE , 过点E画直线EQ∥DN , NP与EQ的交点为点M , 得到四边形DEMN;
②如图2,在菱形ABFG中,顺次连接四边AB , BF , FG , GA的中点D , E , M , N , 得到四边形DEMN.
(2)、请从图1、图2的结论中选择一个进行证明.
25.如图所示,在平面直角坐标系xOy中,B , C两点的坐标分别为 , ,CD⊥y轴于点D , 直线l 经过点D.

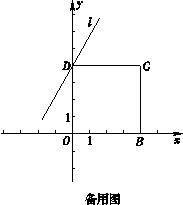 (1)、直接写出点D的坐标;(2)、作CE⊥直线l于点E , 将直线CE绕点C逆时针旋转45°,交直线l于点F , 连接BF.
(1)、直接写出点D的坐标;(2)、作CE⊥直线l于点E , 将直线CE绕点C逆时针旋转45°,交直线l于点F , 连接BF.①依题意补全图形;
②通过观察、测量,同学们得到了关于直线BF与直线l的位置关系的猜想,请写出你的猜想;
③通过思考、讨论,同学们形成了证明该猜想的几种思路:
思路1:作CM⊥CF , 交直线l于点M , 可证△CBF≌△CDM , 进而可以得出 ,从而证明结论.
思路2:作BN⊥CE , 交直线CE于点N , 可证△BCN≌△CDE , 进而证明四边形BFEN为矩形,从而证明结论.
……
请你参考上面的思路完成证明过程.(一种方法即可)
26.如图,在平面直角坐标系xOy中,点 在直线 上,过点 作 ∥y轴,交直线 于点 ,以 为直角顶点, 为直角边,在 的右侧作等腰直角三角形 ;再过点 作 ∥y轴,分别交直线 和 于 , 两点,以 为直角顶点, 为直角边,在 的右侧作等腰直角三角形 ,…,按此规律进行下去,点 的横坐标为 , 点 的横坐标为 , 点 的横坐标为 . (用含n的式子表示,n为正整数)
 27.
27.如图,

在由边长都为1个单位长度的小正方形组成的 正方形网格中,点A , B , P 都在格点上.请画出以AB为边的格点四边形(四个顶点都在格点的四边形),要求同时满足以下条件:
条件1:点P到四边形的两个顶点的距离相等;
条件2:点P在四边形的内部或其边上;
条件3:四边形至少一组对边平行.
(1)、在图①中画出符合条件的一个 ABCD , 使点P在所画四边形的内部;(2)、在图②中画出符合条件的一个四边形ABCD , 使点P在所画四边形的边上;(3)、在图③中画出符合条件的一个四边形ABCD , 使∠D=90°,且∠A≠90°.28.如图,在平面直角坐标系xOy中,动点A(a,0)在x轴的正半轴上,定点B(m, n)在第一象限内(m<2≤a).在△OAB外作正方形ABCD和正方形OBEF , 连接FD , 点M为线段FD的中点.作BB1⊥x轴于点B1 , 作FF1⊥x轴于点F1.
 (1)、填空:由△≌△ , 及B(m, n)可得点F的坐标为 , 同理可得点D的坐标为;(说明:点F , 点D的坐标用含m , n , a的式子表示)(2)、直接利用(1)的结论解决下列问题:
(1)、填空:由△≌△ , 及B(m, n)可得点F的坐标为 , 同理可得点D的坐标为;(说明:点F , 点D的坐标用含m , n , a的式子表示)(2)、直接利用(1)的结论解决下列问题:①当点A在x轴的正半轴上指定范围内运动时,点M总落在一个函数图象上,求该函数的解析式(不必写出自变量x的取值范围);
②当点A在x轴的正半轴上运动且满足2≤a≤8时,求点M所经过的路径的长.