浙教版2019-2020学年初中数学九年级上学期期末复习专题11 图形的相似
试卷更新日期：2019-12-18 类型：复习试卷
一、单选题
-
1. 如果两个相似多边形的面积比是4：9，那么它们的周长比是（ ）A、4：9 B、2：3 C、
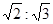D、16：81
2. 如图，取一张长为a，宽为b的长方形纸片，将它对折两次后得到一张小长方形纸片，若要使小长方形与原长方形相似，则原长方形纸片的边a、b应满足的条件是（ ）
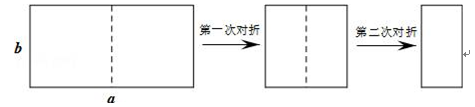A、a= b B、a=2 b C、a=2b D、a=4b3. 如图，下列条件中，不能判定△ACD∽△ABC的是（ ）
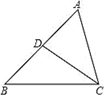A、∠ADC＝∠ACB B、∠B＝∠ACD C、∠ACD＝∠BCD D、4. 如图，平行于BC的直线DE把△ABC分成面积相等的两部分，则 的值为（ ）
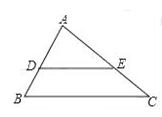A、1 B、 C、
D、
5. 在 中， ，用直尺和圆规在 上确定点 ，使 ，根据作图痕迹判断，正确的是（ ）A、
B、
C、
D、
6. 如图所示，在△ABC中，∠B=70°，AB=4，BC=6，将△ABC沿图示中的虚线DE剪开，剪下的三角形与原三角形相似的有（ ）.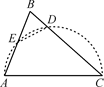
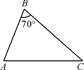
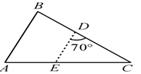
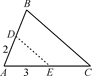
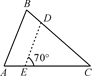A、1个 B、2个 C、3个 D、4个7. 《孙子算经》是中国古代重要的数学著作，成书于约一千五百年前。其中有首歌谣：今有竿不知其长，量得影长一丈五尺，立一标杆，长一尺五寸，影长五寸，问竿长几何？意即：有一根竹竿不知道有多长，量出它在太阳下的影子长丈五尺．同时立一根一尺五寸的小标杆，它的影长五寸(提示：1丈=10尺，1尺=10寸)，则竹竿的长为（ ）
A、五丈 B、四丈五尺 C、一丈 D、五尺8. 如图，P是 ABCD内一点，连结P与 ABCD各顶点， EFGH各顶点分别在边AP、BP、CP、DP上，且AE=2EP，EF∥AB．若△PEF与△PGH的面积和为1，则 ABCD的面积为（ ）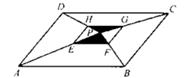
A、4 B、6 C、12 D、189. 小亮要判断△ABC的面积是△DBC的面积的几倍，现仅有一把有刻度的直尺，则至少需要测量的次数是（ ）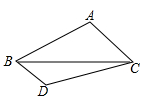
A、1次 B、2次 C、3次 D、4次10. 如图，在矩形ABCD中，E为AB中点，以BE为边作正方形BEFG，边EF交CD于点H，在边BE上取点M使BM＝BC，作MN∥BG交CD于点L，交FG于点N．欧儿里得在《几何原本》中利用该图解释了 ．现以点F为圆心，FE为半径作圆弧交线段DH于点P，连结EP，记△EPH的面积为S1 ， 图中阴影部分的面积为S2 ． 若点A，L，G在同一直线上，则 的值为（ ）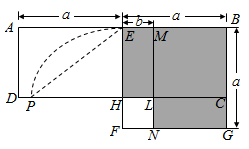
A、 B、 C、 D、二、填空题
-
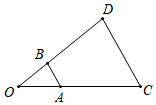
11. 如图，以点O为位似中心，将△OAB放大后得到△OCD，OA=2，AC=3，则 =.
12. 如图，平行四边形ABCD中，E是CD的延长线上一点，BE与AD交于点F，CD=2DE．若△DEF的面积为a，则平行四边形ABCD的面积为（用a的代数式表示）．
13. 如图，在正方形网格上有6个斜三角形：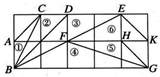
①△ABC，②△CDB，③△DEB，④△FBG，⑤△HGF，⑥△EKF.
在②~⑥中，与①相似的三角形的序号是.(把你认为正确的都填上)
14. 如图是测量玻璃管内径的示意图，点D正对10mm刻度线，点A正对30mm刻度线，DE∥AB．若量得AB的长为6mm，则内径DE的长为mm。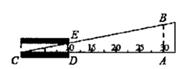
15. 两个等腰直角三角板如图放置，点D为AB的中点．若AG=3，CG=1，则点G、H之间的距离为。
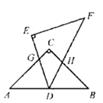16. 三个形状大小相同的菱形按如图所示方式摆放，已知∠AOB＝∠AOE＝90°，菱形的较短对角线长为2cm．若点C落在AH的延长线上，则△ABE的周长为cm．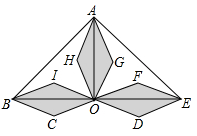
三、解答题
-
17. 如图，已知平行四边形ABCD，E为BC的中点，DE⊥AE.
求证：AB＝ AD.
18. 如图，在△ABC中，AB＝8cm，BC＝16cm，点P从点A开始沿边AB向点B以2cm/s的速度移动，点Q从点B开始沿边BC向点C以4cm/s的速度移动，如果点P、Q分别从点A、B同时出发，经几秒钟△PBQ与△ABC相似？试说明理由．
19. 网格中每个小正方形的边长都是1，
图1 
图2(1)、在图1中画一个格点三角形DEF，使△ABC～△DEF，且相似比为2：1；(2)、在图2中画一个格点三角形PQR，使△ABC～△PQR，且面积比为2：1.20. 如图，四边形ABCD∽四边形A′B′C′D′．
(1)、α＝(2)、求边x、y的长度．21. 如图，△ABC内接于⊙O，AB=AC，∠BAC=36°，过点A作AD∥BC，与∠ABC的平分线交于点D，BD与AC交于点E，与⊙O交于点F.
(1)、求∠DAF的度数；(2)、求证：AE2=EF•ED；22. 如图，已知O是坐标原点，B、C两点的坐标分别为（3，﹣1）、（2，1）．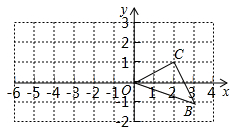
(1)、以0点为位似中心在y轴的左侧将△OBC放大到两倍（即新图与原图的相似比为2），画出图形；(2)、分别写出B、C两点的对应点B′、C′的坐标；(3)、如果△OBC内部一点M的坐标为（x，y），写出M的对应点M′的坐标．23. 根据相似多边形的定义，我们把四个角分别相等，四条边成比例的两个凸四边形叫做相似四边形．相似四边形对应边的比叫做相似比．
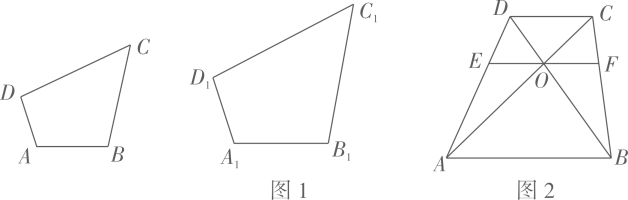(1)、某同学在探究相似四边形的判定时，得到如下三个命题，请判断它们是否正确（直接在横线上填写“真”或“假”）．①条边成比例的两个凸四边形相似；（命题）
②三个角分别相等的两个凸四边形相似；（命题）
③两个大小不同的正方形相似．（命题）
(2)、如图1，在四边形ABCD和四边形A1B1C1D1中，∠ABC＝∠A1B1C1 ， ∠BCD＝∠B1C1D1 ， ，求证：四边形ABCD与四边形A1B1C1D1相似．(3)、如图2，四边形ABCD中，AB∥CD ， AC与BD相交于点O ， 过点O作EF∥AB分别交AD ， BC于点E ， F ． 记四边形ABFE的面积为S1 ， 四边形EFDE的面积为S2 ， 若四边形ABFE与四边形EFCD相似，求 的值．24. 定义：我们知道，四边形的一条对角线把这个四边形分成了两个三角形，如果这两个三角形相似（不全等），我们就把这条对角线叫做这个四边形的“相似对角线”.
理解：
(1)、如图1，已知Rt△ABC在正方形网格中，请你只用无刻度的直尺在网格中找到一点D，使四边形ABCD是以AC为“相似对角线”的四边形（保留画图痕迹，找出3个即可）；(2)、如图2，在四边形ABCD中，∠ABC=80°，∠ADC=140°，对角线BD平分∠ABC.求证：BD是四边形ABCD的“相似对角线”；
(3)、如图3，已知FH是四边形EFCH的“相似对角线”，∠EFH=∠HFG=30°，连接EG，若△EFG的面积为2 ，求FH的长.