浙教版2019-2020学年初中数学九年级上学期期末复习专题10 比例线段
试卷更新日期:2019-12-18 类型:复习试卷
一、单选题
-
1. 已知 ,则 等于( )A、 B、 C、2 D、32. 若 (xy≠0),则下列比例式成立的是( )
A、 B、 C、 D、3. 在长度为1的线段上找到两个黄金分割点P,Q,则PQ=( )A、 B、 C、 D、4. 若 ,且 ,则 的值是( )A、4 B、2 C、20 D、145. 四条线段 , , , 成比例,其中 , , ,则 ( )A、2㎝ B、4㎝ C、6㎝ D、8㎝6. 下面四条线段中,是成比例线段的是( )A、3cm、6cm、8cm、9cm B、3cm、6cm、9cm、l8cm C、3cm、6cm、7cm、9cm D、3cm、5cm、6cm、9cm7. 已知点C在线段AB上,且点C是线段AB的黄金分割点(AC>BC),则下列结论正确的是( )A、AB2=AC•BC B、BC2=AC•BC C、AC= BC D、BC= AC8. 已知 ,则直线 一定经过的象限是( )A、第一、三、四象限 B、第一、二、四象限 C、第一、四象限 D、第二、三象限9. 如图,点 B 在线段 AC 上,且 ,设BC=1,则AC的长是( )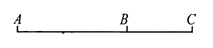 A、 B、 C、 D、10. 在欧几里得的《几何原本》中给出一个找线段的黄金分割点的方法.如图所示,以线段AB为边作正方形ABCD,取AD的中点E,连结BE,延长DA至F,使得EF=BE,以AF为边作正方形AFGH,则点H即是线段AB的黄金分割点.若记正方形AFGH的面积为S1 , 矩形BCIH的面积为S2 , 则S1 与S2的大小关系是( )
A、 B、 C、 D、10. 在欧几里得的《几何原本》中给出一个找线段的黄金分割点的方法.如图所示,以线段AB为边作正方形ABCD,取AD的中点E,连结BE,延长DA至F,使得EF=BE,以AF为边作正方形AFGH,则点H即是线段AB的黄金分割点.若记正方形AFGH的面积为S1 , 矩形BCIH的面积为S2 , 则S1 与S2的大小关系是( )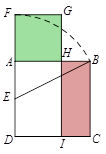 A、
A、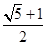 B、
B、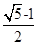 C、
D、1
C、
D、1
二、填空题
-
11. 若x是3和6的比例中项,则x=.12. 线段a=4,线段b=9,线段c是线段a与线段b的比例中项,则线段c=13. 在比例尺为1:10000000的地图上,相距7.5cm的两地A、B的实际距离为千米.14. 若a:b:c=1:2:3,则
15. 如果把两条邻边中较短边与较长边的比值为 的矩形称作黄金矩形.那么,现将长度为20 的铁丝折成一个黄金矩形,这个黄金矩形较短的边长是 .16. 黄金分割具有严格的比例性,蕴藏着丰富的美学价值,这一比值能够引起人们的美感.如图,连接正五边形ABCDE的各条对角线围成一个新的五边形MNPQR.图中有很多顶角为36°的等腰三角形,我们把这种三角形称为“黄金三角形”,黄金三角形的底与腰之比为 .若MN= -1,则AB= .
三、解答题
-
17. 已知:如图,△ABC∽△ADE , AB=15,AC=9,BD=5.求AE .
 18. 若P在线段AB上,点Q在AB的延长线上, ,且 ,求PQ的长.
18. 若P在线段AB上,点Q在AB的延长线上, ,且 ,求PQ的长.
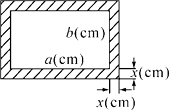
19. 实践证明,节目主持人站在舞台的黄金分割点处音响效果及审美效果最好.如下图,假设线段AB为舞台前沿,你能为主持人找出一个最佳位置C吗? 20. 如图,一个矩形剪去一个以宽为边长的正方形后,剩下的矩形长与宽的比与原矩形长与宽的比相等,求原矩形的长与宽的比.
20. 如图,一个矩形剪去一个以宽为边长的正方形后,剩下的矩形长与宽的比与原矩形长与宽的比相等,求原矩形的长与宽的比. 21. 已知线段a、b、c满足a:b:c=3:2:6,且a+2b+c=26.
21. 已知线段a、b、c满足a:b:c=3:2:6,且a+2b+c=26.
(1)、求a、b、c的值;(2)、若线段x是线段a、b的比例中项,求x的值.
22.
(1)、已知 = ≠0,求代数式 的值;(2)、已知线段AB=10cm,点C、点D是线段AB的两个不同黄金分割点,
求C、D之间的距离.