浙教版2019-2020学年初中数学九年级上学期期末复习专题9 弧长与扇形面积
试卷更新日期:2019-12-18 类型:复习试卷
一、单选题
-
1. 若一个扇形的半径是 ,且它的弧长是 ,则此扇形的圆心角等于( )A、 B、 C、 D、2. 一个扇形的半径为6,圆心角为120°,则该扇形的面积是( )A、2π B、4π C、12π D、24π3. 如图,在扇形 中, 为弦, , , ,则 的长为( )
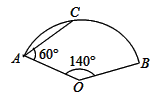 A、 B、 C、 D、4. 如图,已知AB是⊙O的直径,若∠BAC=60°,AC=3,则 的长为( )
A、 B、 C、 D、4. 如图,已知AB是⊙O的直径,若∠BAC=60°,AC=3,则 的长为( )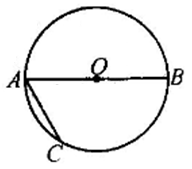 A、4π B、2π C、 π D、π5. 德国数学家高斯在大学二年级时得出了正十七边形是尺规作图法,并给出了可用尺规作图的正多边形的条件.下面是高斯正十七边形作法的一部分:“如图,已知AB是圆O的直径,分别以A,B为圆心、AB长为半径作弧,两弧交于点C,D两点…”.若AB长为2,则图中弧CAD的长为( )
A、4π B、2π C、 π D、π5. 德国数学家高斯在大学二年级时得出了正十七边形是尺规作图法,并给出了可用尺规作图的正多边形的条件.下面是高斯正十七边形作法的一部分:“如图,已知AB是圆O的直径,分别以A,B为圆心、AB长为半径作弧,两弧交于点C,D两点…”.若AB长为2,则图中弧CAD的长为( ) A、 B、 C、 D、6. 如图,正方形ABCD中,分别以B,D为圆心,以正方形的边长a为半径画弧,形成树叶形(阴影部分)图案,则树叶形图案的周长为( )
A、 B、 C、 D、6. 如图,正方形ABCD中,分别以B,D为圆心,以正方形的边长a为半径画弧,形成树叶形(阴影部分)图案,则树叶形图案的周长为( )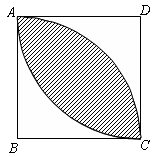 A、
A、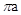 B、
B、 C、
C、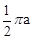 D、
D、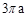 7. 如图,在半径为6的⊙O中,点A,B,C都在⊙O上,四边形OABC是平行四边形,则图中阴影部分的面积为( )
7. 如图,在半径为6的⊙O中,点A,B,C都在⊙O上,四边形OABC是平行四边形,则图中阴影部分的面积为( )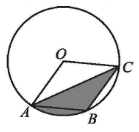 A、6π B、 π C、 π D、2π8. 文艺复兴时期,意大利艺术大师达·芬奇曾研究过圆弧所围成的许多图形的面积问题. 如图所示称为达·芬奇的“猫眼”,可看成圆与正方形的各边均相切,切点分别为 , 所在圆的圆心为点 (或 ). 若正方形的边长为2,则图中阴影部分的面积为( )
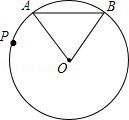
A、6π B、 π C、 π D、2π8. 文艺复兴时期,意大利艺术大师达·芬奇曾研究过圆弧所围成的许多图形的面积问题. 如图所示称为达·芬奇的“猫眼”,可看成圆与正方形的各边均相切,切点分别为 , 所在圆的圆心为点 (或 ). 若正方形的边长为2,则图中阴影部分的面积为( )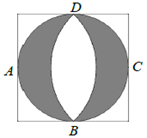 A、 B、2 C、 D、9. 如图,PA,PB与⊙O相切,切点分别为A,B,PA=3,∠BPA=60°,若BC为⊙O的直径,则图中阴影部分的面积为( )
A、 B、2 C、 D、9. 如图,PA,PB与⊙O相切,切点分别为A,B,PA=3,∠BPA=60°,若BC为⊙O的直径,则图中阴影部分的面积为( )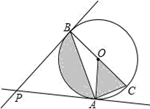 A、3π B、π C、2π D、10. 如图,由六段相等的圆弧组成的三叶花,每段圆弧都是四分之一圆周,OA=OB=OC=2,则这朵三叶花的面积为( )
A、3π B、π C、2π D、10. 如图,由六段相等的圆弧组成的三叶花,每段圆弧都是四分之一圆周,OA=OB=OC=2,则这朵三叶花的面积为( )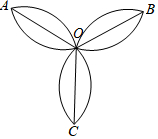 A、3π–3 B、3π–6 C、6π–3 D、6π–6
A、3π–3 B、3π–6 C、6π–3 D、6π–6二、填空题
-
11. 如果一个扇形的弧长等于它的半径,那么此扇形称为“等边扇形”,则半径为3的“等边扇形”的面积为.12. 如图,分别以正三角形的3个顶点为圆心,边长为半径画弧,三段弧围成的图形称为莱洛三角形.若正三角形边长为6cm,则该莱洛三角形的周长为cm.
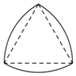 13. 如图是一个圆锥的主视图,根据图中标出的数据(单位: ),计算这个圆锥侧面展开图圆心角的度数为 .
13. 如图是一个圆锥的主视图,根据图中标出的数据(单位: ),计算这个圆锥侧面展开图圆心角的度数为 .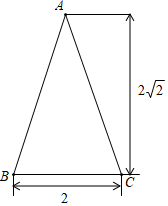 14. 如图, 是半圆 的直径, ,则 的长为.
14. 如图, 是半圆 的直径, ,则 的长为. 15. 如图, , ,以点 为圆心, 为半径作弧交 于点 ,点 ,交 于点 ,若 ,则阴影部分的面积为.
15. 如图, , ,以点 为圆心, 为半径作弧交 于点 ,点 ,交 于点 ,若 ,则阴影部分的面积为.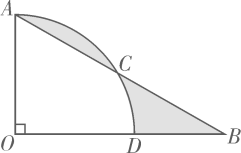 16. 如图,在正方形ABCD的边长为3,以A为圆心,2为半径作圆弧.以D为圆心,3为半径作圆弧.若图中阴影部分的面积分为 、 .则 =。
16. 如图,在正方形ABCD的边长为3,以A为圆心,2为半径作圆弧.以D为圆心,3为半径作圆弧.若图中阴影部分的面积分为 、 .则 =。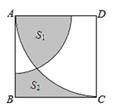
三、解答题
-
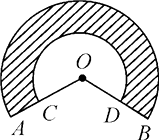
17. 如图,阴影部分是一广告标志,已知两圆弧所在圆的半径分别是20cm,10cm,∠AOB=120°,则这个广告标志的周长是多少?
 18. 如图,AB是⊙O的直径,弦CD⊥AB于E,∠CDB=30°,CD= ,求阴影部分的面积.
18. 如图,AB是⊙O的直径,弦CD⊥AB于E,∠CDB=30°,CD= ,求阴影部分的面积.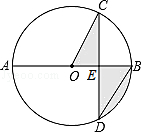 19. 制造弯形管道时,经常要先按中心线计算“展直长度”,再备料.下图是一段管道,其中直管道部分AB的长为3 000mm,弯形管道部分BC,CD弧的半径都是1 000mm,∠O=∠O’=90°,计算图中中心虚线的长度.
19. 制造弯形管道时,经常要先按中心线计算“展直长度”,再备料.下图是一段管道,其中直管道部分AB的长为3 000mm,弯形管道部分BC,CD弧的半径都是1 000mm,∠O=∠O’=90°,计算图中中心虚线的长度.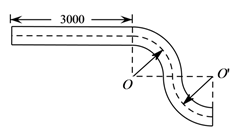 20. 如图,在正方形网格中,每个小正方形的边长都为1
20. 如图,在正方形网格中,每个小正方形的边长都为1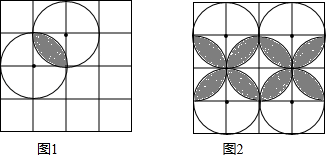 (1)、如图1,两个半径为1的圆相交,则阴影部分的面积为;(2)、图2是以(1)中的图形为基本图形,通过一组图形变换得到的,这组变换可以是.(写出一组即可)(填入序号).①轴对称变换;②平移变换;③旋转变换.21. 如图,AB是圆O的直径,弦AC=2,∠ABC=30°.
(1)、如图1,两个半径为1的圆相交,则阴影部分的面积为;(2)、图2是以(1)中的图形为基本图形,通过一组图形变换得到的,这组变换可以是.(写出一组即可)(填入序号).①轴对称变换;②平移变换;③旋转变换.21. 如图,AB是圆O的直径,弦AC=2,∠ABC=30°.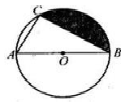 (1)、求证:(2)、求图中阴影部分的面积.22. 如图,AB为⊙O的直径,CD是弦,AB⊥CD于点E,OF⊥AC于点F,BE=OF.
(1)、求证:(2)、求图中阴影部分的面积.22. 如图,AB为⊙O的直径,CD是弦,AB⊥CD于点E,OF⊥AC于点F,BE=OF.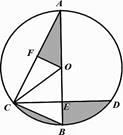 (1)、求证:△AFO≌△CEB;(2)、若BE=4,CD = 求:
(1)、求证:△AFO≌△CEB;(2)、若BE=4,CD = 求:①⊙O的半径;
②求图中阴影部分的面积.